🔥博客主頁: 【小扳_-CSDN博客】
❤感謝大家點贊👍收藏⭐評論✍


文章目錄
1.0 判斷合法
1.1 使用遍曆方式實現驗證二叉搜索樹
1.2 使用遞歸方式實現驗證二叉搜索樹
2.0 求範圍和
2.1 使用非遞歸實現二叉搜索樹的範圍和
2.2 使用遞歸方式實現二叉搜索樹的範圍和
3.0 根據前序遍曆結果建樹
3.1 使用非遞歸實現前序遍曆構造二叉搜索樹
3.2 使用遞歸實現前序遍曆構造二叉搜索樹
4.0 二叉搜索樹的最近祖先
4.1 使用遍曆方式實現二叉搜索樹的最近公共祖先
5.0 本篇二叉搜索樹實現 LeetCode 經典題的完整代碼
1.0 判斷合法
題目:
給你一個二叉樹的根節點 root ,判斷其是否是一個有效的二叉搜索樹。
有效 二叉搜索樹定義如下:
節點的左子樹隻包含 小于 當前節點的數。
節點的右子樹隻包含 大于 當前節點的數。
所有左子樹和右子樹自身必須也是二叉搜索樹。
示例 1:
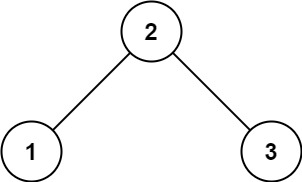
輸入:root = [2,1,3]
輸出:trueOJ鏈接:98. 驗證二叉搜索樹
1.1 使用遍曆方式實現驗證二叉搜索樹
具體思路爲:利用中序遍曆的效果,若每一個節點的值都比前一個節點的值大,則符合二叉搜索樹;若出現某一個節點或者多個節點的值比前一個節點的值大,則符合二叉搜索樹。
代碼如下:
//使用遍曆實現驗證二叉樹
public boolean isValidBST2(TreeNode node) {
Stack stack = new Stack();
TreeNode p = node;
long prev = Long.MIN_VALUE;
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
}else {
TreeNode pop = stack.pop();
if(pop.val = root.val) {
return false;
}
prev = root.val;
return isValidBST(root.right);
}2.0 求範圍和
題目:
給定二叉搜索樹的根結點 root,返回值位于範圍 [low, high] 之間的所有結點的值的和。
示例 1:
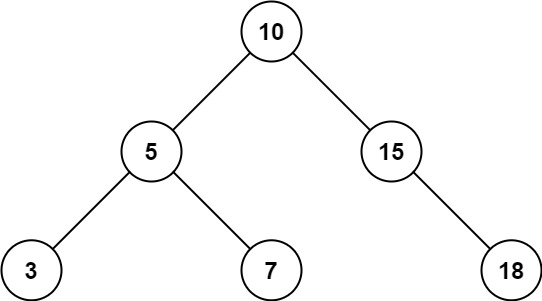
輸入:root = [10,5,15,3,7,null,18], low = 7, high = 15
輸出:32OJ鏈接:938. 二叉搜索樹的範圍和
2.1 使用非遞歸實現二叉搜索樹的範圍和
具體思路爲:利用中序遍曆效果,對于滿足 node.val > slow && node.val high 時,則直接返回 sum 結果即可。
代碼如下:
//使用非遞歸求二叉搜索樹的範圍和
public int rangeSum2(TreeNode root,int slow,int high) {
Stack stack = new Stack();
TreeNode p = root;
int sum = 0;
while(p != null || !stack.isEmpty()) {
if(p != null) {
stack.push(p);
p = p.left;
}else {
TreeNode pop = stack.pop();
if(pop.val > high) {
break;
}
if(pop.val >= slow) {
sum += pop.val;
}
p = pop.right;
}
}
return sum;
}2.2 使用遞歸方式實現二叉搜索樹的範圍和
具體思路爲:首先考慮符合 slow 與 high 範圍之内的節點值,需要返回當前節點的值與該節點的左子樹與右子樹的符合範圍的節點值。再來考慮不符合 slow 與 high 範圍之内的節點值時,當 node.val slow ,則不能往該節點的右子樹繼續遞歸下去了,需要往該節點的左子樹遞歸尋找符合範圍值的節點。
代碼如下:
//使用遞歸求二叉搜索樹的範圍和
public int rangeSum(TreeNode root,int slow, int high) {
if(root == null) {
return 0;
}
if(root.val high) {
return rangeSum(root.left,slow,high);
}
return root.val + rangeSum(root.left,slow,high) +
rangeSum(root.right,slow,high);
}3.0 根據前序遍曆結果建樹
題目:
給定一個整數數組,它表示BST(即 二叉搜索樹 )的 先序遍曆 ,構造樹并返回其根。
保證 對于給定的測試用例,總是有可能找到具有給定需求的二叉搜索樹。
二叉搜索樹 是一棵二叉樹,其中每個節點, Node.left 的任何後代的值 嚴格小于 Node.val , Node.right 的任何後代的值 嚴格大于 Node.val。
二叉樹的 前序遍曆 首先顯示節點的值,然後遍曆Node.left,最後遍曆Node.right。
示例 1:
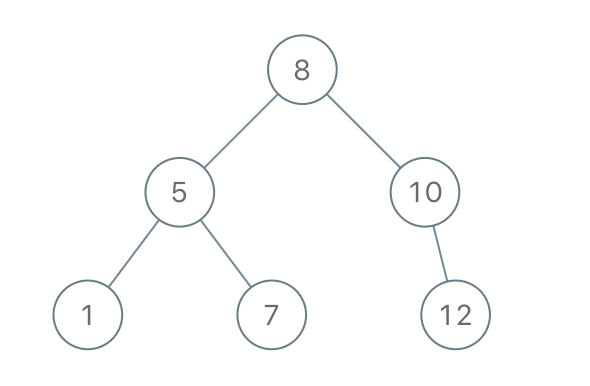
輸入:preorder = [8,5,1,7,10,12]
輸出:[8,5,10,1,7,null,12]OJ鏈接:1008. 前序遍曆構造二叉搜索樹
3.1 使用非遞歸實現前序遍曆構造二叉搜索樹
具體思路爲:利用數組中第一個值作爲根節點的值,再遍曆數組從索引 1 開始直到該數組長度 - 1 。得到每一個數組的值來創建一個新的節點,再自定義 insert 方法将該節點插入二叉搜索樹中。關鍵的是:使用非遞歸方式實現該方法,首先定義一個 parent 變量,用來記錄 p 的父親節點,循環遍曆 p ,若 p.val > node.val 時,先記錄 parent = p,再 p = p.left ;若 p.val parent.val,則 parent.right = node;若 node.val
代碼如下:
//根據前序遍曆的結果建樹
public TreeNode bstFromPreorder(int[] preorder) {
TreeNode root = new TreeNode(preorder[0]);
for(int i = 1; i node.val) {
parent = p;
p = p.left;
}
}
if(parent.val > node.val) {
parent.left = node;
}else {
parent.right = node;
}
}3.2 使用遞歸實現前序遍曆構造二叉搜索樹
具體思路爲:遞歸遍曆直到遇到 node == null 時,那麽 node = new TreeNode(val) 。若 node.val > val 時,向左子樹遞歸下去 node = node.left;若 node.val
代碼如下:
//根據前序遍曆的結果建樹
public TreeNode bstFromPreorder(int[] preorder) {
TreeNode root = new TreeNode(preorder[0]);
for(int i = 1; i val) {
node.left = insert(node.left,val);
}else {
node.right = insert(node.right,val);
}
return node;
}4.0 二叉搜索樹的最近祖先
題目:
給定一個二叉搜索樹, 找到該樹中兩個指定節點的最近公共祖先。
百度百科中最近公共祖先的定義爲:“對于有根樹 T 的兩個結點 p、q,最近公共祖先表示爲一個結點 x,滿足 x 是 p、q 的祖先且 x 的深度盡可能大(一個節點也可以是它自己的祖先)。”
例如,給定如下二叉搜索樹: root = [6,2,8,0,4,7,9,null,null,3,5]
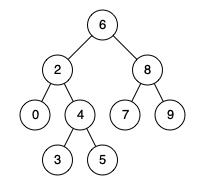
示例 1:
輸入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
輸出: 6
解釋: 節點 2 和節點 8 的最近公共祖先是 6。OJ鏈接:235. 二叉搜索樹的最近公共祖先
4.1 使用遍曆方式實現二叉搜索樹的最近公共祖先
具體思路爲:若 p 與 q 在當前節點的左右子樹,那麽該節點就是該 q 與 p 的公共最近的祖先;若 p 與 q 在當前節點的同一側(都在該當前節點的左子樹或者右子樹),則需要繼續往下遍曆,當 node.val p.val && node.val > q.val 都需要繼續遍曆,直到跳出循環後,則當前節點 node 就是該 p 與 q 的公共最近節點。
代碼如下:
//二叉搜索樹的最近祖宗
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode a = root;
while(p.val a.val && q.val > a.val) {
if(p.val
5.0 本篇二叉搜索樹實現 LeetCode 經典題的完整代碼
import java.util.Stack;
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
//使用遞歸實現驗證二叉樹
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) {
return true;
}
boolean l = isValidBST(root.left);
if (!l) {
return false;
}
if(prev >= root.val) {
return false;
}
prev = root.val;
return isValidBST(root.right);
}
//使用遍曆實現驗證二叉樹
public boolean isValidBST2(TreeNode node) {
Stack stack = new Stack();
TreeNode p = node;
long prev = Long.MIN_VALUE;
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
}else {
TreeNode pop = stack.pop();
if(pop.val high) {
return rangeSum(root.left,slow,high);
}
return root.val + rangeSum(root.left,slow,high) + rangeSum(root.right,slow,high);
}
//使用非遞歸求二叉搜索樹的範圍和
public int rangeSum2(TreeNode root,int slow,int high) {
Stack stack = new Stack();
TreeNode p = root;
int sum = 0;
while(p != null || !stack.isEmpty()) {
if(p != null) {
stack.push(p);
p = p.left;
}else {
TreeNode pop = stack.pop();
if(pop.val > high) {
break;
}
if(pop.val >= slow) {
sum += pop.val;
}
p = pop.right;
}
}
return sum;
}
//根據前序遍曆的結果建樹
public TreeNode bstFromPreorder(int[] preorder) {
TreeNode root = new TreeNode(preorder[0]);
for(int i = 1; i node.val) {
parent = p;
p = p.left;
}
}
if(parent.val > node.val) {
parent.left = node;
}else {
parent.right = node;
}
}
//使用遞歸的方式
public TreeNode insert(TreeNode node, int val) {
if (node == null) {
return new TreeNode(val);
}
if (node.val > val) {
node.left = insert(node.left,val);
}else {
node.right = insert(node.right,val);
}
return node;
}
//二叉搜索樹的最近祖宗
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode a = root;
while(p.val a.val && q.val > a.val) {
if(p.val
本篇爲相關二叉搜索樹對于 LeetCode 題目的相關解法,希望對你有所幫助。









