前言
欢迎来到小K的数据结构专栏的第十一小节,本节将为大家带来堆的详解并带来堆题目的讲解(✨当然也为大家准备了完整的源码 )~希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🐾
目录
- 前言
- 一、满二叉树
- 二、完全二叉树
- 三、_堆
- 四、总结
✨在讲堆之前我们先看看满二叉树和完全二叉树~
一、满二叉树
我们先来看看满二叉树的特性:
- 是一颗二叉树
- 每一颗子树要么没有孩子要么有两个孩子
- 叶子结点在同一层
✨如下就是一颗满二叉树,少了任何一个叶子结点它就不是(除非直接少了一层–——>)
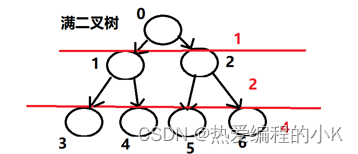
✨从上图划分的层级关系,我们一眼可以看出:
- 第n层节点数量一定是2(n-1)个,比如第三次就是2的平方,4个节点
- 有m层的满二叉树的节点总数为2m-1个,比方说上图的二叉树节点总数就为23-1=7个
✨前面我们讲的树、二叉树、二叉查找树都是用链式结构描述的,那还有没有别的方法?答案是当然有~我们今天就用数组结构来描述!!!,既然要用数组来描述,那肯定要知道数组下标和树相应层级的对应关系,第一个1个空间表示第一层,第二个两个代表第二层,以此类推…

✨我们就按顺序给满二叉树标号,作为下标,下面我们通过表格来观察一下他们有什么特点:
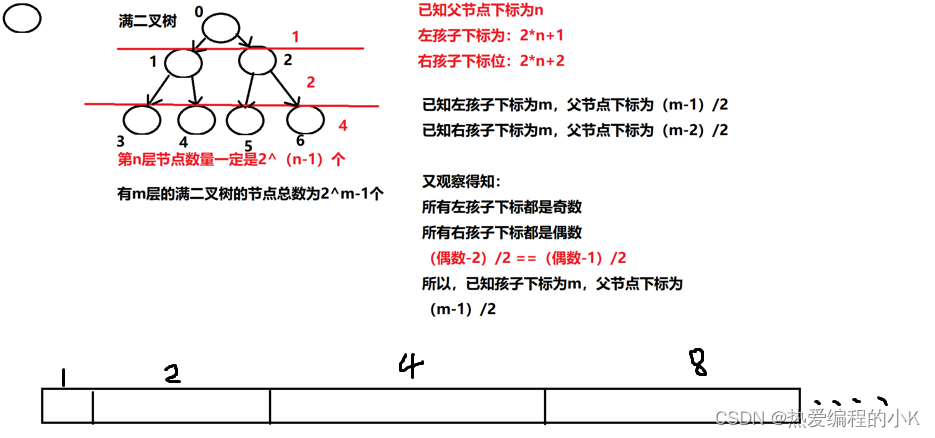
父 左孩子 右孩子 0 1 2 1 3 4 2 5 6 … … … - 根据上图,如果已知父节点下标为n,左孩子下标为2n+1,右孩子下标为2n+2
- 那么如果已知左孩子下标为m,父节点下标为(m-1)/2,同理已知右孩子,则父节点下标为(m-2)/2
- 又观察得知所有左孩子的下标都是奇数,所有右孩子的下标为偶数且(偶数-1)/2==(偶数-2)/2
- 所以已知孩子下标为m,父节点下标为(m-1)/2
附上下图:
二、完全二叉树
完全二叉树的特性:
- 是一颗二叉树
- 满二叉树从最下一层从右往左删(删除顺序和阅读顺序相反)
- 同样满足父节点和孩子节点的下标关系:已知孩子下标为m,父节点下标为(m-1)/2
所以说,满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
✨接下来我们用线性结构来描述一下完全二叉树:
很简单,我们准备一个结构体,里面存一个数组和计算计算数组大小的元素,插入直接按顺序插入
#define MAX 1024 typedef struct three { int size; int all_Binarythree[MAX]; }three; void init(three* t) { //memset(t->all_Binarythree, 0, MAX); t->size = 0; } void insert(three* t, int insertData) { t->all_Binarythree[t->size++] = insertData; }
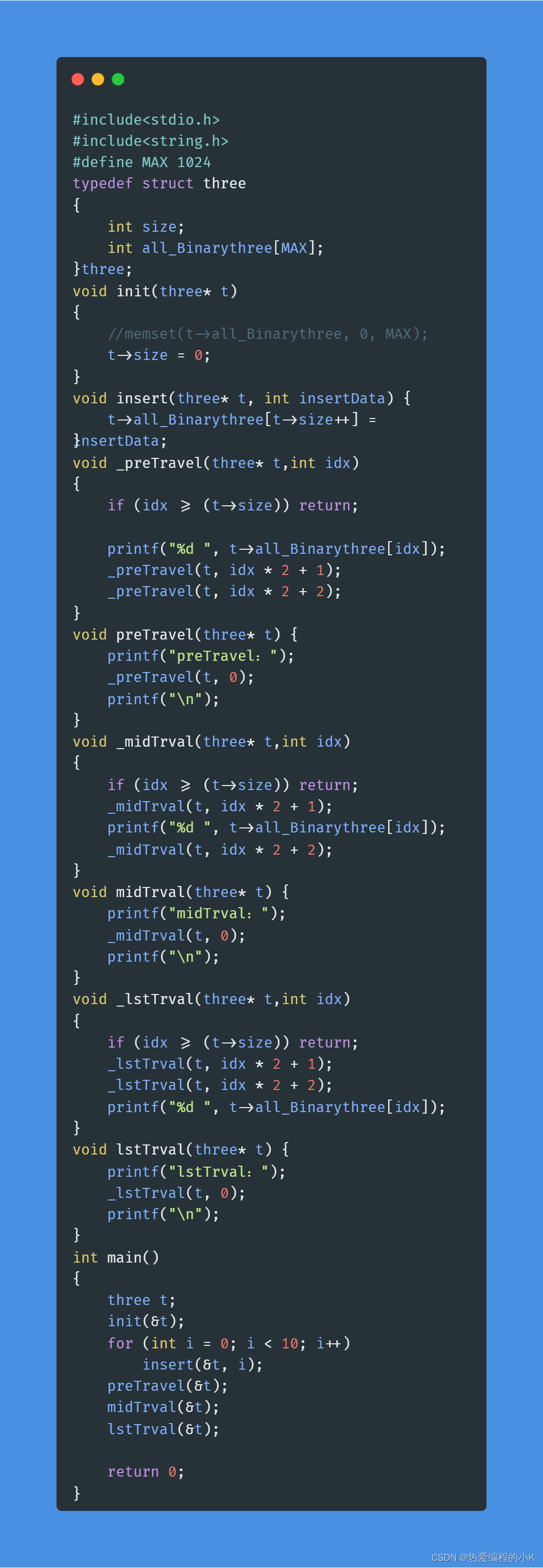
✨发现完全吻合,没问题~附上源代码:
三、_堆
✨堆:父子之间有序的完全二叉树,如下图就是堆,父节点都小于孩子节点
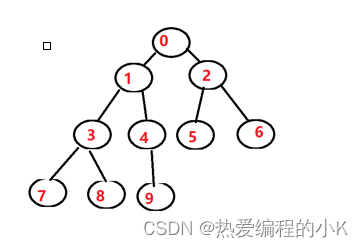
父大于子 大顶堆 最大堆
父小于子 小顶堆 最小堆
第一步,✨堆插入
✨堆插入思想:
- 数组方式进入
- 往上(父子)线条上作插入排序
- 先临时保存新数据
- 循环和父节点比较,如果不冲突,循环结束
- 如果冲突,当前位置父节点数据覆盖当前位置
- 临时保存的数据覆盖当前位置
堆插入思想过程
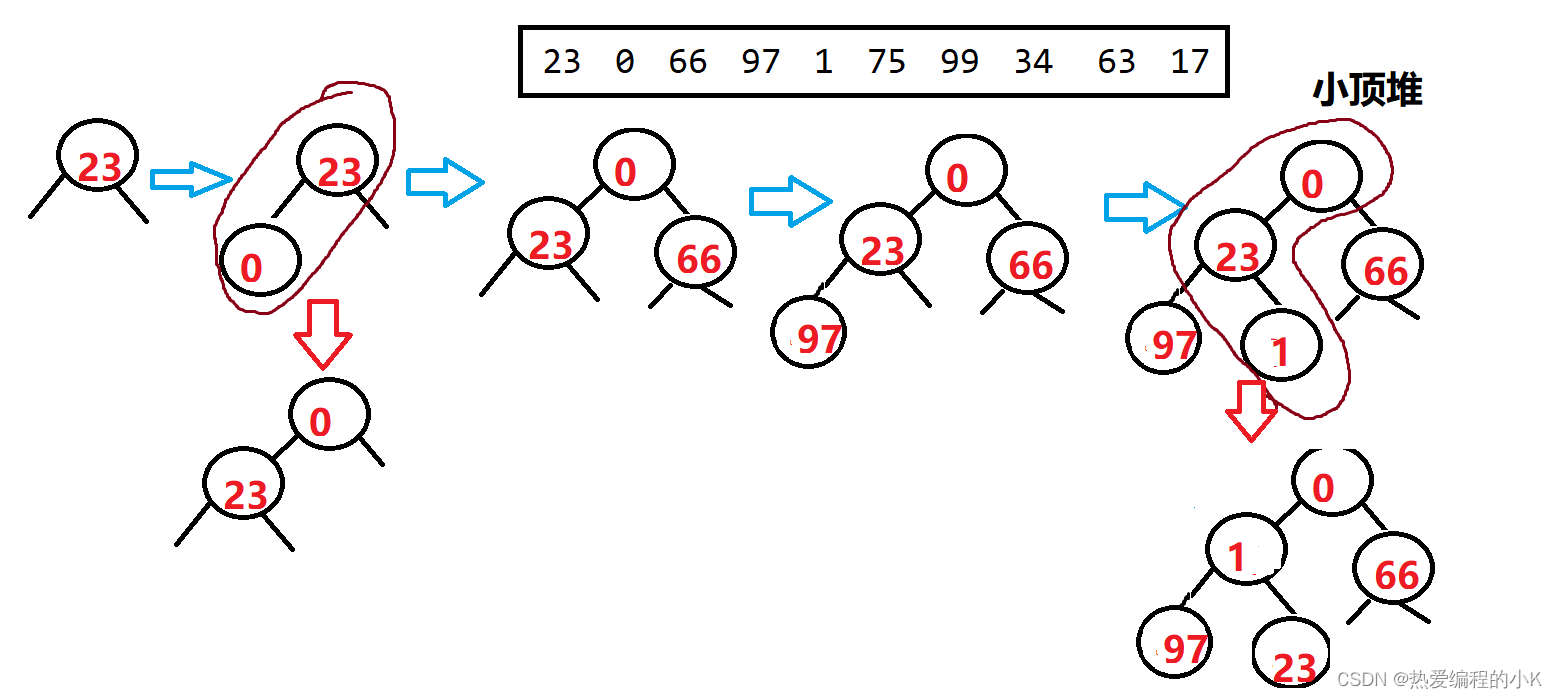
✨详解代码:
void insert(myHeap* t, int insertData) { //需要新开内存 if ((t->size) >= (t->maxSize)) { //计算新开内存 (t->maxSize) += ((t->maxSize >> 1 > 1) ? (t->maxSize >> 1) : 1); //新开内存 int* pTemp = (int*)malloc(sizeof(int) * (t->maxSize)); assert(pTemp); if (t->pRoot) { memcpy(pTemp, (t->pRoot), sizeof(int) * (t->size)); free(t->pRoot); } t->pRoot = pTemp; } //insertData放入动态数组中,元素个数加1 t->pRoot[t->size++] = insertData; //循环遍历,父子一条线 //当前节点下标 int currentIdx = t->size - 1; //父节点下标 int partentIdx; while (1) { if (currentIdx pRoot[currentIdx]) pRoot[partentIdx])) t->pRoot[currentIdx] = t->pRoot[partentIdx]; else break; //循环继续 currentIdx = partentIdx; } //覆盖回来 t->pRoot[currentIdx] = insertData; }第二步,✨堆删除
删除堆顶元素思想:
-
临时保存堆顶元素
-
用最后一个元素覆盖堆顶元素
-
从堆顶开始往下循环
-
越界循环结束
-
最小孩子大于最后一个数据结束循环
-
最小孩子不大于最后一个数据,那就子覆盖父(孩子中最小的接替父节点)
-
循环结束后,最后一个节点覆盖当前位置
-
size–
-
返回堆顶元素
✨删除过程如下:
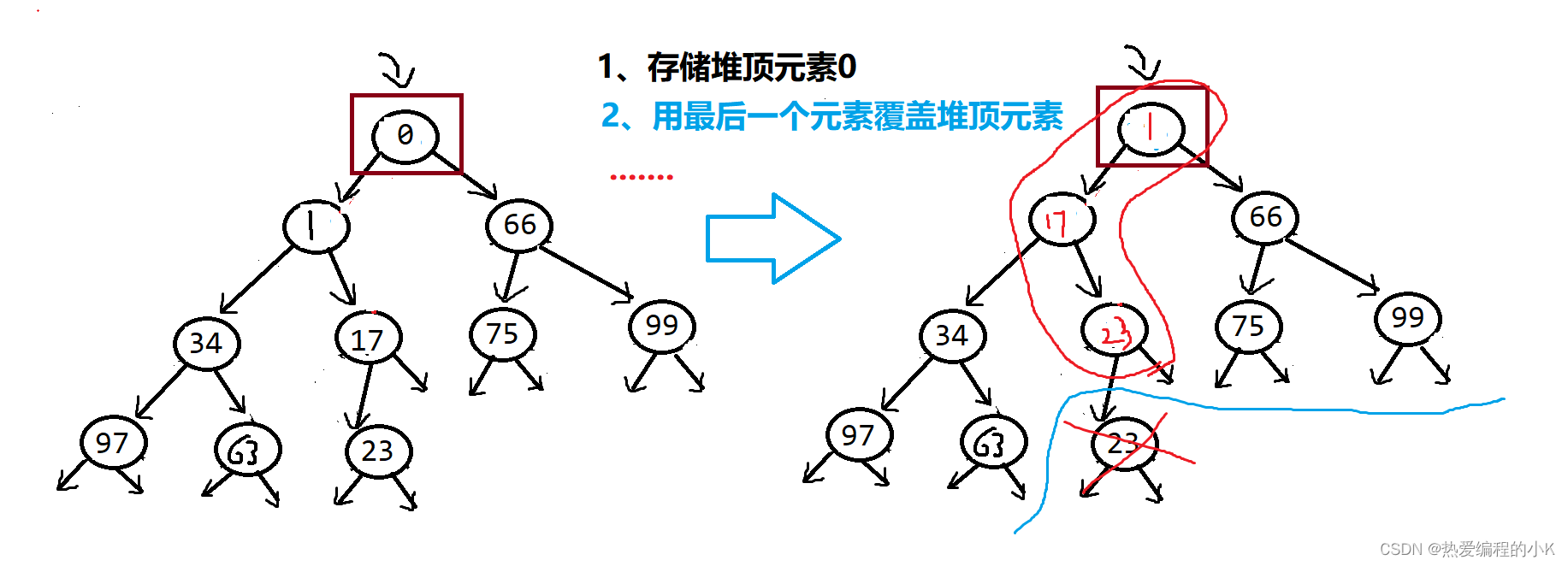
代码详解:
int pop(myHeap* t) { if (0 == t->size) return -666666; //1. 临时保存堆顶元素 int delData = t->pRoot[0]; if (1 == t->size) { t->size = t->maxSize = 0; free(t->pRoot); t->pRoot = NULL; return delData; } //2. 用最后一个元素覆盖堆顶元素 t->pRoot[0] = t->pRoot[t->size - 1]; //3. 从堆顶开始往下循环 //当前点下标 int currentIdx = 0; //最小孩子下标 int minchildIdx; while (1) { //越界循环结束 if ((currentIdx * 2 + 2) > (t->size-1)) break; //求最小孩子 //假设左孩子为最小孩子 minchildIdx = currentIdx * 2 + 1; if (t->pRoot[minchildIdx] > t->pRoot[minchildIdx + 1]) minchildIdx++; //最小孩子大于最后一个数据结束循环 if (t->pRoot[minchildIdx] > t->pRoot[t->size - 1]) break; //最小孩子不大于最后一个数据,那就子覆盖父(孩子中最小的接替父节点) t->pRoot[currentIdx] = t->pRoot[minchildIdx]; //循环 currentIdx = minchildIdx; } //4. 循环结束后,最后一个节点覆盖当前位置 t->pRoot[currentIdx] = t->pRoot[t->size - 1]; //5. size-- t->size--; //6. 返回堆顶元素 return delData; }✨结果演示:
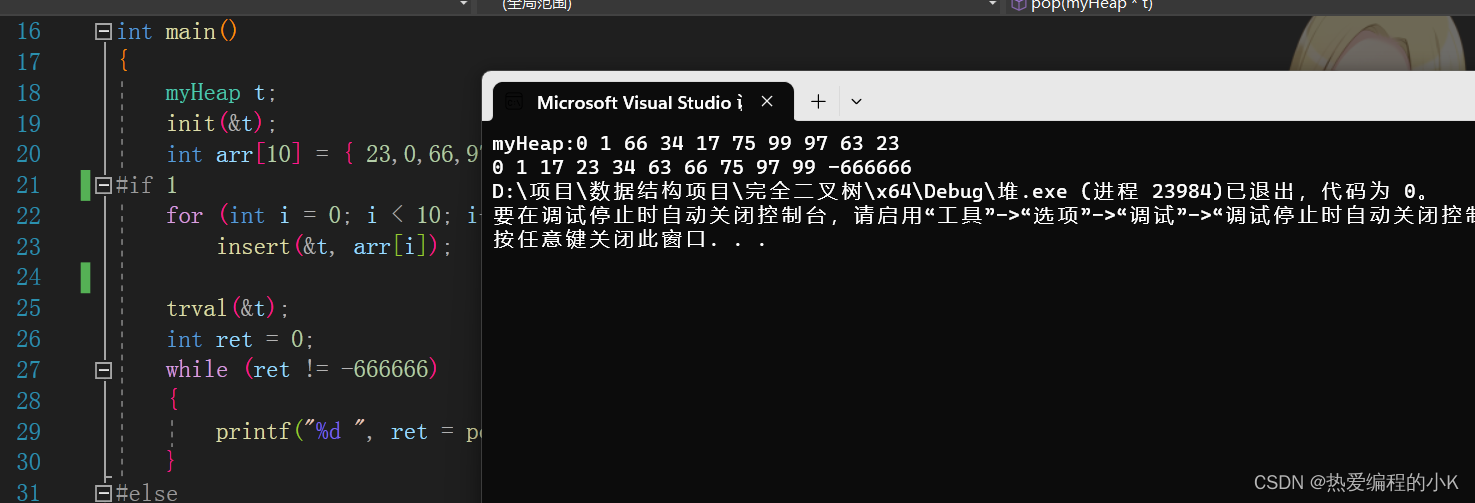
我们发现删除之后输出就变得有序了,这似乎和我们接下来将要讲的堆排序有点相似
第三步,✨堆排序
你猜对了,不是相似~就是
✨堆排序:
- 无序数组用堆插入思想插入
- 用删除堆顶思想删除
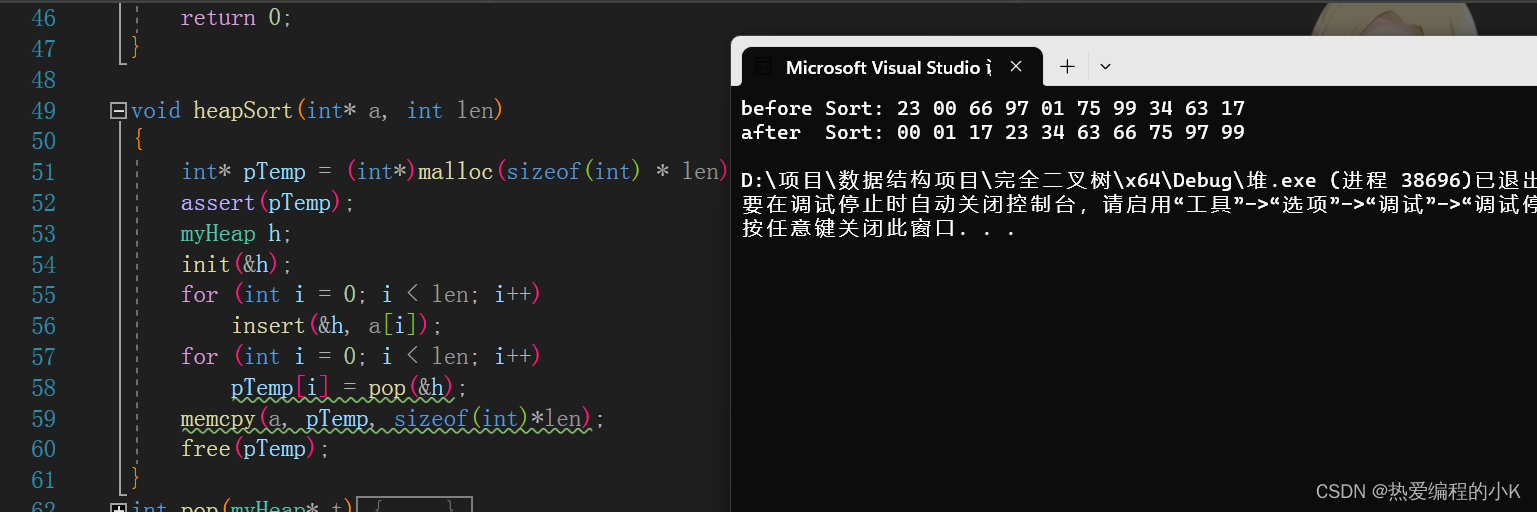
✨堆排序代码详解:
void heapSort(int* a, int len) { int* pTemp = (int*)malloc(sizeof(int) * len); assert(pTemp); myHeap h; init(&h); for (int i = 0; i✨综合代码:

第四步,✨堆排序实际应用,Leetcode——215. 数组中的第K个最大元素
✨题目
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
✨ 示例 1:
输入: [3,2,1,5,6,4], k = 2 输出: 5
✨示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
✨ 提示:
- 1 int left = i * 2 + 1, right = i * 2 + 2, largest = i; if (left
-









