既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上物联网嵌入式知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、电子书籍、讲解视频,并且后续会持续更新
需要这些体系化资料的朋友,可以加我V获取:vip1024c (备注嵌入式)
如果你需要这些资料,可以戳这里获取
(一)问题描述
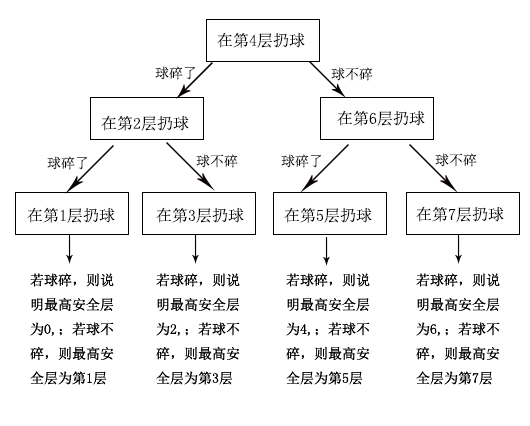
给定N层楼和i个球。用i个球检测在这N层楼中的某一层t球扔下楼时不碎,而在t+1层球扔下楼时会碎,则t层称为最高安全层。求用i个球一定可以检测N层楼的最高安全层的最少扔球次数。(注:球不碎还可以再用)
Example:
给定i=3个球,检测N=7层楼,最优的情况如下:
由上图可得最少的扔球次数为3。
(二)问题求解思路
下面给定两个思路:
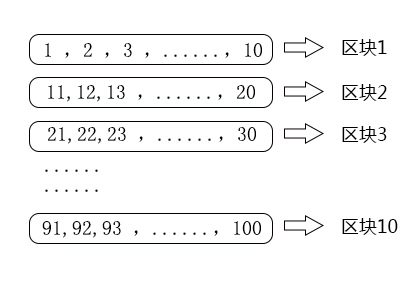
(一)分块思想:举个例子,i=2,N=100
现在设想着你手头只有一个球,那么很显然,你只能从最底层(即第一层)一层一层地往上试,那么考虑最坏情况(即最高安全层在第100层),最大的扔球次数就是100,可见在整个过程中我们只能逐层的尝试,否则在任何一层上球碎了,我们就不能准确的确定最高安全楼层了。(一个球的尝试方法是暴力而且简单的,但对于两个球的情况会有所启示)
我们现在考虑有两个球的情况下,那么我们可以尝试用第一个球来确定一个较小的范围,而第二个球则在这个范围内逐层去尝试(由只一个球的尝试方法得到的启示)。
这时我们很容易的想到将100分成10个10层,第一个球用来确认在哪个10层里,第二个球用来确认具体层数。具体来说就是,拿着第一个球从第10层尝试,只要没碎就再上10层,直至碎了或者爬到楼顶,这样确定了十位数的范围。然后再用第二个球逐层尝试。如第一个球:在第10层扔下没碎,那就在第20层,扔下还是没碎,那就在第30层,扔下还是没碎,继续往上10层,假设在第40层扔下碎了;那么就拿第二个球从31层至39层开始依次逐层尝试,直至排查出最高安全楼层为止。大致思路如下:
这种思法已经比较接近答案了,但你会发现还有问题。比如如果球最高安全楼层为16或者96,用刚刚那个想法的话,这两种情况的总尝试次数并不一样:最高安全楼层为16时,第一个球试了2次就定位了区块;而最高安全楼层为96时,第一个球试了10次才定位了区块。虽然在区块内部的第二个球的逐层尝试是一样的,但96层对应的总尝试次数就多得太多了。原因就是10*10的区块均匀划分对大数不利。
尝试的次数是受到两个因素的制约的:1第一个球选择哪一个分块所用的尝试次数;2第二个球逐层尝试的次数。个因为碎和不碎这两种状态是不对称的,所以第一个球的尝试的过程只能从小数逐渐尝试到大数,而不能反着来。所以均匀划分区块对大数是不公平。
明白了这个缺陷,也就知道了改进的基本思想:还是要对100找出一种二维区块划分,但不是均匀划分。对于比较小的楼层部分,其包含的楼层范围可以适当多;越向大数部分走,其包含的楼层范围越来越小。从下往上,每一个区块内所含楼层递减。
对于最高安全楼层比较低的情况,第一个球试的次数少;所以最高安全楼层比较高的情况,则让第二个球试的次数少。用第二个球的尝试次数的减少来弥补第一个球需要尝试的次数的递增,使两个球在不同维度上的尝试次数达到一种微妙的平衡。
按照这个思路,要把上面那个均匀的区块切分改进如下:
那么这里的x和n会是多少呢?最后一个区块里包含1个楼层,倒数第二个包含2个楼层,倒数第三个包含3个楼层,继续,各区块包含的楼层是4,5,6,……
于是问题转变为,到包含多少个楼层的时候,100个楼层全部分配完?由于1+2+3+……+13=91,而1+2+3+……+14=105,就是说从1开始累加,加到14时,总和第一次大于100:所以上图里的x是14。
问题解决:第一个球依次试14,27,39,50,60,69,77,84,90,95,99,100。中间任何一次破碎了,就从上一次的下一层开始用第二个球逐层尝试,直至第二个球也破碎为止。用这个方法,总次数一定不超过14次:当最高安全楼层越来越高时,第一个球试的次数越来越多,但第二个球试的次数越来越少,两者始终维持着一种平衡。
该思路简单易懂,但当球的的个数(即i的值)增加的时候,分块的会变得越来越难。
本思路参考:
http://mp.weixin.qq.com/s?__biz=MzAxOTc5MDY2NA==&mid=2651974453&idx=1&sn=d94b02b4e36f579320930f5117fd540e&mpshare=1&scene=23&srcid=0426FhZVbioCW1nCHE97kt4X#rd
(二)动态规划思想
下面提供两个方案:
方案一:
一.方案概述
dp(i,j):表示用i个球测试j层楼一定可测出某一层是最高安全层的最少次数,等同于min{ max{ 1+dp(i-1,k-1),1+dp(i,j-k) },0