一、基本思想
动态规划法将待求解问题分解成若干个相互重叠的子问题,每个子问题相互关联;动态规划法与分治法的区别就在于分治法的子问题相互不关联,而动态规划法的子问题是相互关联的,且有重叠的部分。
二、算法分析
动态规划法求多段图的最短路径,根据起始节点,寻找与该节点相连且路径最短的那个节点,以寻找到的结点以起始节点,找下一个与其路径最短的那个节点,判断这三个节点之间是否还有一组解,比我们第一次找到的路径还要短,若存在,且是最短的,则将上一组解替换为我们找到的最优解,依次找出其他节点的最短路径,直至最后一个点,那么得出的解就是本问题的最优解。
for (j = 1;j = 0;i--) {//前驱节点
if (cost[i] + node[i][j]
三、问题描述
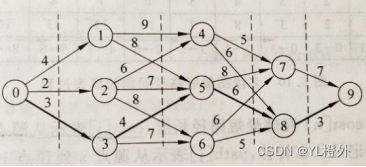
四、代码实现
#include
using namespace std;
#define INF 999//宏定义常量
int node[100][100]; // 最多100个点
int CreateGraph()
{
int point, edge;
cout point >> edge;
for (int i = 0;i > weight;
node[i][j] = weight;
}
return point;
}
// 求 n个顶点的多段图的最短路径
int Path(int n)
{
int i, j;
int cost[100], path[100]; // 存储路径长度和路径
for (i = 1;i = 0;i--) {//前驱节点
if (cost[i] + node[i][j] 








