后端开发AI与机器学习: 应用与集成

1.背景介绍

随着数据量的不断增加，人工智能和机器学习技术在各个领域的应用也逐渐成为主流。后端开发人员需要掌握这些技术，以便在开发过程中更好地集成和应用。本文将介绍后端开发人员在AI和机器学习领域的核心概念、算法原理、实例代码和未来发展趋势等方面的内容。

2.核心概念与联系

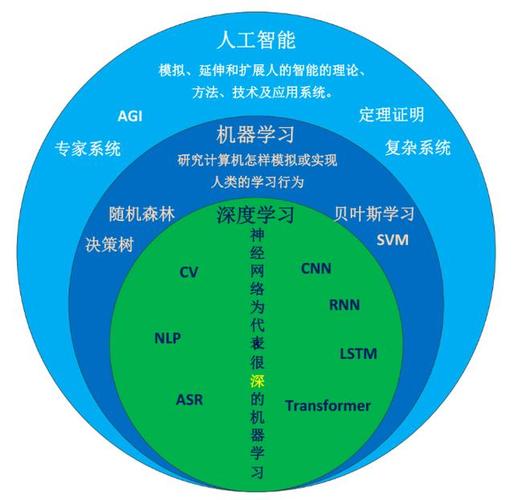
2.1 AI与机器学习的定义与区别

人工智能(Artificial Intelligence，AI)是一种试图使计算机具有人类智能的技术。机器学习(Machine Learning，ML)是人工智能的一个子领域，它涉及到计算机通过学习自主地改善其解决问题的能力。

2.2 常见的机器学习算法

机器学习算法可以分为监督学习、无监督学习和强化学习三类。

• 监督学习(Supervised Learning)：算法通过被标注的数据来学习任务，并在新的数据上进行预测。常见算法有线性回归、逻辑回归、支持向量机、决策树等。
• 无监督学习(Unsupervised Learning)：算法通过没有标注的数据来学习任务，并在新的数据上进行分类或聚类。常见算法有K均值、DBSCAN、自组织图等。
• 强化学习(Reinforcement Learning)：算法通过与环境的互动来学习任务，并在新的环境中进行决策。常见算法有Q-学习、深度Q网络等。

  3.核心算法原理和具体操作步骤以及数学模型公式详细讲解

  3.1 线性回归

  线性回归(Linear Regression)是一种简单的监督学习算法，用于预测连续变量。其目标是找到最佳的直线(或多项式)来拟合数据。

  3.1.1 数学模型

  线性回归的数学模型如下：

  $$ y = \beta0 + \beta1x1 + \beta2x2 + \cdots + \betanx_n + \epsilon $$

  其中，$y$ 是目标变量，$x1, x2, \cdots, xn$ 是输入变量，$\beta0, \beta1, \beta2, \cdots, \beta_n$ 是权重，$\epsilon$ 是误差。

  3.1.2 最小二乘法

  线性回归的目标是最小化误差的平方和，即最小化以下公式：

  $$ \sum{i=1}^{n}(yi - (\beta0 + \beta1x{1i} + \beta2x{2i} + \cdots + \betanx_{ni}))^2 $$

  通过求解这个公式的梯度下降，可以得到权重的最优值。

  3.2 逻辑回归

  逻辑回归(Logistic Regression)是一种对数回归的扩展，用于预测二分类变量。

  3.2.1 数学模型

  逻辑回归的数学模型如下：

  $$ P(y=1) = \frac{1}{1 + e^{-(\beta0 + \beta1x1 + \beta2x2 + \cdots + \betanx_n)}} $$

  其中，$P(y=1)$ 是目标变量的概率，$x1, x2, \cdots, xn$ 是输入变量，$\beta0, \beta1, \beta2, \cdots, \beta_n$ 是权重。

  3.2.2 最大似然估计

  逻辑回归的目标是最大化似然函数，即最大化以下公式：

  $$ \prod{i=1}^{n}P(yi=1)^{yi}(1-P(yi=1))^{1-y_i} $$

  通过求解这个公式的梯度下降，可以得到权重的最优值。

  3.3 支持向量机

  支持向量机(Support Vector Machine，SVM)是一种强大的分类和回归算法，可以处理高维数据和非线性问题。

  3.3.1 核函数

  支持向量机可以通过核函数(Kernel Function)将线性不可分的问题转换为高维的可分问题。常见的核函数有径向向量(Radial Basis Function，RBF)、多项式(Polynomial)和线性(Linear)核。

  3.3.2 最优解

  支持向量机的目标是最小化以下公式：

  $$ \min{\mathbf{w},b}\frac{1}{2}\mathbf{w}^T\mathbf{w}+C\sum{i=1}^{n}\xi_i $$

  其中，$\mathbf{w}$ 是权重向量，$b$ 是偏置项，$\xi_i$ 是松弛变量。

  通过求解这个公式的Lagrange乘子方法，可以得到权重的最优值。

  3.4 K均值

  K均值(K-Means)是一种无监督学习算法，用于分类和聚类问题。

  3.4.1 算法步骤

  1. 随机选择$K$个样本点作为初始的聚类中心。
  2. 根据样本与聚类中心的距离，将每个样本分配到最近的聚类中心。
  3. 重新计算每个聚类中心的位置，使其为该聚类中的样本的平均位置。
  4. 重复步骤2和3，直到聚类中心的位置不再变化或达到最大迭代次数。

  3.4.2 距离度量

  K均值算法可以使用欧氏距离(Euclidean Distance)或曼哈顿距离(Manhattan Distance)作为样本与聚类中心的距离度量。

  4.具体代码实例和详细解释说明

  4.1 线性回归

  ```python import numpy as np

  生成随机数据

  X = np.random.rand(100, 1) y = 3 * X.squeeze() + 2 + np.random.rand(100, 1)

  初始化权重

  beta0 = 0 beta1 = 0

  学习率

  learning_rate = 0.01

  迭代次数

  iterations = 1000

  训练线性回归模型

  for _ in range(iterations): ypred = beta0 + beta1 * X error = y - ypred gradientbeta0 = -2 * (error.sum()) / len(error) gradientbeta1 = -2 * X.dot(error) / len(error) beta0 -= learningrate * gradientbeta0 beta1 -= learningrate * gradientbeta1

  预测

  Xtest = np.array([[0.5], [1.5]]) print("预测结果:", beta0 + beta1 * Xtest) ```

  4.2 逻辑回归

  ```python import numpy as np

  生成随机数据

  X = np.random.rand(100, 1) y = 1 * (X > 0.5) + 0

  初始化权重

  beta0 = 0 beta1 = 0

  学习率

  learning_rate = 0.01

  迭代次数

  iterations = 1000

  训练逻辑回归模型

  for _ in range(iterations): ypred = beta0 + beta1 * X error = y - ypred gradientbeta0 = -2 * (error * (1 - ypred) * (ypred > 0.5)).sum() / len(error) gradientbeta1 = -2 * X.dot(error * (1 - ypred) * (ypred > 0.5)).sum() / len(error) beta0 -= learningrate * gradientbeta0 beta1 -= learningrate * gradientbeta1

  预测

  Xtest = np.array([[0.5], [1.5]]) print("预测结果:", 1 * (beta0 + beta1 * Xtest > 0.5)) ```

  4.3 支持向量机

  ```python from sklearn import datasets from sklearn.modelselection import traintest_split from sklearn.preprocessing import StandardScaler from sklearn.svm import SVC

  加载数据

  iris = datasets.load_iris() X, y = iris.data, iris.target

  数据分割

  Xtrain, Xtest, ytrain, ytest = traintestsplit(X, y, testsize=0.2, randomstate=42)

  数据标准化

  scaler = StandardScaler() Xtrain = scaler.fittransform(Xtrain) Xtest = scaler.transform(X_test)

  训练支持向量机模型

  svm = SVC(kernel='linear', C=1) svm.fit(Xtrain, ytrain)

  预测

  ypred = svm.predict(Xtest) print("准确率:", svm.score(Xtest, ytest)) ```

  4.4 K均值

  ```python from sklearn.cluster import KMeans from sklearn.datasets import make_blobs

  生成数据

  X, _ = makeblobs(nsamples=300, centers=4, clusterstd=0.60, randomstate=0)

  训练K均值模型

  kmeans = KMeans(nclusters=4, randomstate=0) kmeans.fit(X)

  预测

  ypred = kmeans.predict(X) print("聚类中心:", kmeans.clustercenters) print("每个样本所属的聚类:", ypred) ```

  5.未来发展趋势与挑战

  随着数据规模的增加和计算能力的提高，AI和机器学习技术将更加普及和强大。未来的趋势和挑战包括：

  • 大规模数据处理：如何高效地处理和存储大规模数据，以及如何在分布式环境中进行机器学习。
  • 解释性AI：如何让AI模型更加可解释，以便用户更好地理解其决策过程。
  • 人工智能伦理：如何在开发人工智能系统时考虑道德、隐私和法律等问题。
  • 跨学科合作：人工智能技术将越来越多地与其他领域相结合，如生物信息学、物理学和化学等。

    6.附录常见问题与解答

    6.1 什么是过拟合？如何避免过拟合？

    答：过拟合是指模型在训练数据上表现良好，但在新数据上表现不佳的现象。为避免过拟合，可以采取以下方法：

    • 增加训练数据
    • 减少特征的数量
    • 使用正则化方法
    • 使用更简单的模型

      6.2 什么是欠拟合？如何避免欠拟合？

      答：欠拟合是指模型在训练数据和新数据上表现均不佳的现象。为避免欠拟合，可以采取以下方法：

      • 增加特征的数量
      • 使用更复杂的模型
      • 调整模型参数

        6.3 什么是交叉验证？

        答：交叉验证是一种用于评估模型性能的方法，它涉及将数据分为多个部分，然后逐一将其中的一部分作为测试数据，余下的部分作为训练数据，重复这个过程，最后计算模型在所有测试数据上的平均性能。