🐓 时间复杂度
常用排序的时间复杂度
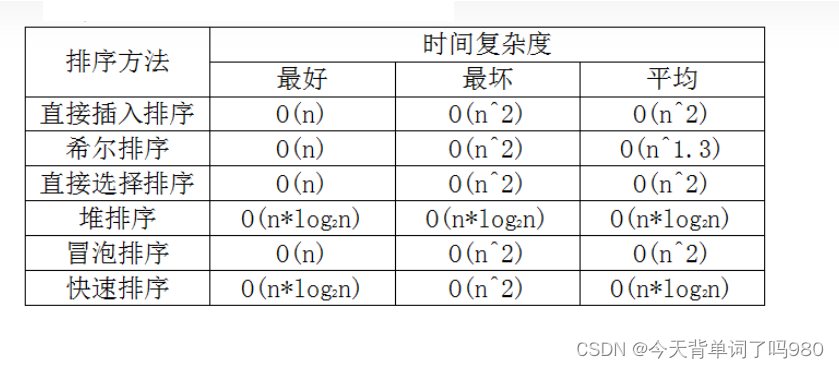
时间频度
算法需要花费的时间,和它语句执行的次数是成正比的,所以会把一个算法种语句执行次数称为语句频度和时间频度、记作T(n)。
定义
时间复杂度就是找到一个无限接近时间频度T(n)同数量级的函数,当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度
通俗一点就是找到一个和T(n)同一量级的函数F(n),写作O(f(n)),一般在程序中我们会看最内层或者说其执行次数最多的代码行。
时间复杂度计算
时间复杂度中O是受T(n)种n变化次数最多的那一项影响,比如:T(n) = n^3+n^2+n+23 那这个最大的影响项就是O( n^3)
常见的时间复杂度
阶数
| 执行次数函数举例 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| n^2+2n+1 | O(n^2) | 平方阶 |
| 5log2n+20 | O(logn)/log2n | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| n^3+n^2+3n+4 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
大小排序
消耗时间从小到大
O(1)
🐓 实例
常数阶O(1)
没有任何循环等复杂结构,时间复杂度就是O(1)常量阶
代码示例:
int a = 1; //O(1) int b = 1; //O(1) int t = a + b; //该行执行了O(1)次,故O(1)
对数阶O(log₂n)
在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2n也就是说当循环 log2n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(log2n)
代码示例:
int i = 1; while (i









