目录
系列文章目录
一、问题
二、实验思路综述
1.实验工具及算法
2.实验数据
3.实验目标
4.实验步骤
三、最小二乘问题引入
1.最小二乘问题样例
2.最小二乘问题解决方案及数学模型化
3.相关线性代数知识导入
3.1 梯度
3.2 矩阵的逆
3.3 QR分解
四、最小二乘法
1.定义
2.数学模型化
2.1 目标函数
2.2 最小二乘法的解
2.3 列向量空间的意义
3.目标求解推导
4.正规方程
4.1 通过Gram矩阵求解正规方程
4.2 通过QR分解求解正规方程
5.编程实践
5.1 QR分解
5.2 求最优解
五、梯度下降法
1.定义
2.目标函数推导
3.操作与算法流程
4.编程实践
4.1 迭代次数
4.2 相邻迭代解之间的“相对接近程度”
5.不同情况解的分析及误差对比
5.1 不同算法分析
5.2 误差分析
5.3 效率对比
6.不同语言与平台对求解的影响
六、理论补充与应用拓展
1.最小二乘法
1.1 线性回归定义与算法步骤
1.2 最小二乘法的应用
2.梯度下降法
2.1 BP神经网络
2.2 梯度下降法的应用
七、实验小结
1.最小二乘问题求解总结
2.参考资料
系列文章目录
本系列博客重点在最优化方法的概念原理与代码实践(有问题欢迎在评论区讨论指出,或直接私信联系我)。
代码可以全抄 大家搞懂原理与流程去复现才是有意义的!!!
第一章 最优化方法——K-means实现手写数字图像聚类_@李忆如的博客-CSDN博客
第二章 最优化方法——QR分解_@李忆如的博客-CSDN博客
第三章 最优化方法——最小二乘法
梗概
本篇博客主要介绍最小二乘法、梯度下降法的原理与流程,分别使用Matlab、Pycharm分别实现了最小二乘法、不同迭代停止条件的梯度下降法等方法对给定优化模型进行求解并进行解之间的误差分析对比,并进行了一定理论与应用(内附数据集和python及Matlab代码)。
一、问题
读取附件“MatrixA_b.mat”文件中的矩阵A和向量b。建立关于矩阵, 向量,未知向量最小二乘优化模型:
1)通过最小二乘法的正规方程,求出优化模型的准确解;
2)利用梯度下降法迭代求出模型“近似解”,通过设置迭代停止条件,分析“近似解”与“准确解”之间的误差。
二、实验思路综述
1.实验工具及算法
本次实验分别使用Matlab、Pycharm分别实现了最小二乘法、不同迭代停止条件的梯度下降法等方法对给定优化模型进行求解并进行解之间的误差分析对比。
2.实验数据
本次实验使用给定矩阵A(50x40)与向量b(50x1)组成的优化模型进行实验内容的探究,在拓展内容的探究与尝试中使用了部分网络数据集。
3.实验目标
本次实验要求使用不同方法对给定优化模型(最小二乘问题)进行求解并进行解的误差分析及对比。此外,本人还在相关理论方面进行了补充,对算法应用进行了实践。
4.实验步骤
本次实验大致流程如表1所示:
表1 实验3流程
| 1.实验思路综述 |
| 2.最小二乘问题的引入 |
| 3. 最小二乘法的推导与求解 |
| 4. 梯度下降法的推导与求解 |
| 5. 不同情况解的分析及误差对比 |
| 6. 理论拓展与应用实践 |
三、最小二乘问题引入
1.最小二乘问题样例
在求解最小二乘问题前,我们需要对其进行定义与数学模型化,故本部分引入一个二维样例如图1所示,一个实际的测量问题如图2所示:
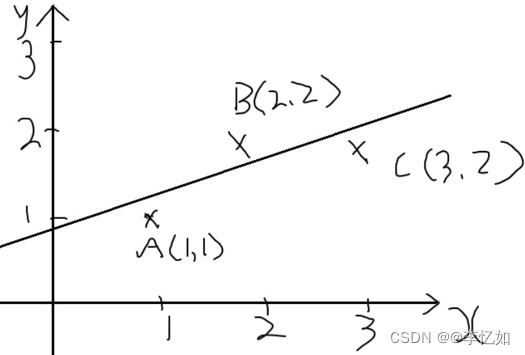
图1 二维最小二乘问题样例

图2 实际最小二乘问题样例
分析:对于图1的问题,无法找到一条直线同时经过A、B、C三点,对于图2的问题,我们无法求解出一组满足条件的x1,x2,x3。
2.最小二乘问题解决方案及数学模型化
最小二乘问题:由于各种误差,难以求得满足问题条件的一组解(无法通过现有数据拟合出一条过所有数据的线或超平面)的问题。
解决方案:对于最小二乘法,核心的解决方案就是寻找该问题的近似解。并尽可能逼近原问题的目标,使残差向量r=Ax-b在某种度量下尽可能小。最小二乘问题数学模型化如图3所示:

图3 最小二乘问题模型
3.相关线性代数知识导入
在后续需要用不同方法求解最小二乘问题,在此对核心相关线性代数知识进行一定补充。
3.1 梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
梯度求解样例如式1所示:
式1 梯度求解样例
3.2 矩阵的逆
当一个矩阵X满足XA=I时,X被称为A的左逆,同理可以定义右逆。
矩阵的逆:如果矩阵A存在左逆和右逆,则左逆和右逆一定相等,此时X称为矩阵的逆(矩阵非奇异),记作A^-1。
逆存在的判断:对于一个矩阵的逆是否存在,有如表2中所示五种常用方法:
表2 逆矩阵存在判断常用方法
| 1.若矩阵行列式不为0,可逆 |
| 2.若矩阵的秩为n,可逆 |
| 3.若存在一个矩阵B,使AB=BA=I,可逆 |
| 4.对于齐次方程AX=0,若方程只有零解,可逆 |
| 5.对于非齐次线性方程AX=b,若方程只有特解,可逆 |
矩阵逆的常用证明框架如图4所示:

图4 矩阵逆的证明框架
补充:性质(a)对任意矩阵A都成立,性质(b)对方阵矩阵A都成立。
逆矩阵求解:在编程实现中矩阵求逆一般使用库函数,在不同语言中均进行了打包,如matlab中可使用inv()求逆矩阵,用法详见:矩阵求逆 - MATLAB inv - MathWorks 中国,用pinv()求伪逆,用法详见:Moore-Penrose 伪逆 - MATLAB pinv - MathWorks 中国
3.3 QR分解
QR分解是将一个矩阵A分解成具有标准正交列向量的矩阵Q和上三角矩阵R(对角线元素不为0)的算法。这个分解能够有效的提高计算机求解线性方程、最小二乘问题、带约束的最小二乘问题的效率,有效降低计算复杂度,QR分解形式如图5所示。

图5 QR分解定义形式
QR分解根据原理分为Gram-Schmidt、Householder、Givens三种实现方法,经本人实验2探究发现,对于较稠密矩阵,使用Householder QR分解有较高的效率与稳定性。
四、最小二乘法
在本部分对于最小二乘法的定义、数学模型化、目标求解推导、模型求解做详解。
1.定义
最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域也得到广泛应用。
2.数学模型化
2.1 目标函数
结合最小二乘问题模型与最小二乘法定义,将最小二乘法数学模型化,故对于给定的给定A∈R^mxn,b∈R^m,求解x∈R^n让目标函数最小,目标函数如式2所示:
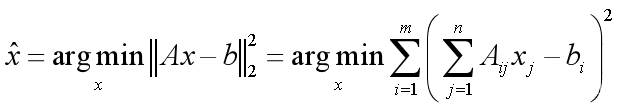
式2 最小二乘法目标函数
2.2 最小二乘法的解
结合最小二乘法的原理,对于式2的目标函数求解,得到的x应该满足式3的条件:

式3 最小二乘法的解的条件
分析:当残差r=Ax−b=0时,则x是线性方程组Ax=b的解;否则其为误差最小平方和下方程组的近似解。
2.3 列向量空间的意义
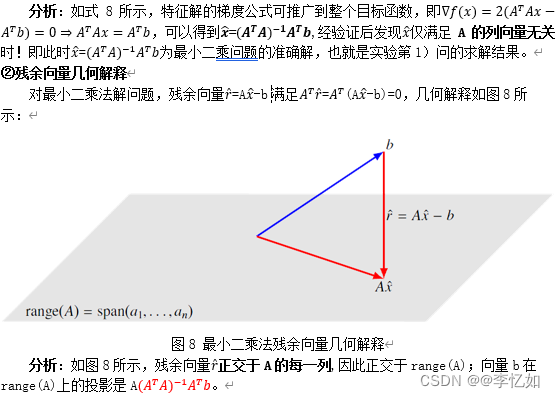
对于满足最小二乘法目标函数式2的解x,其列向量空间的意义如图6所示:

图6 最小二乘法列向量空间的意义
分析:如图6所示,Ax∈range(A)中最接近b的向量,r=Ax-b正交(垂直)于值域空间range(A)。
3.目标求解推导
对于最小二乘法的目标函数式2,我们需要得到满足式3条件的最优解x。由于目标函数f(x)为可微函数,故最优解x满足梯度∇f(x)=0,如式4所示:
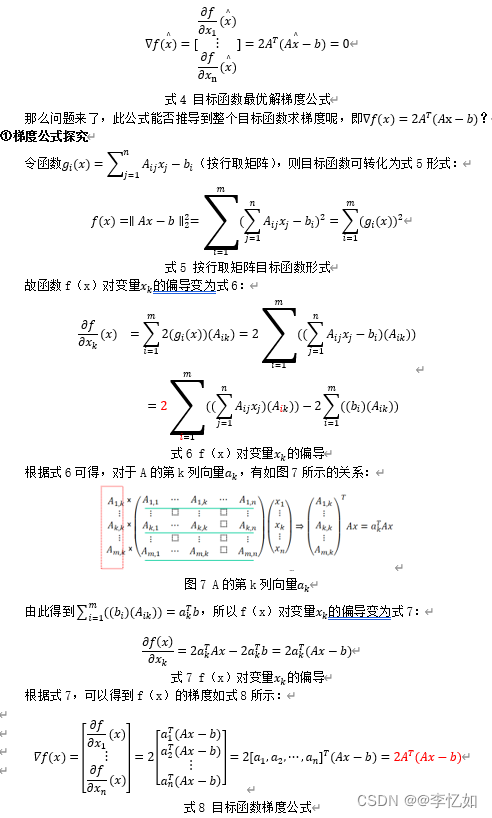
4.正规方程
由最小二乘法定义与梯度公式求导可知,我们需要找到目标函数的最优解即找梯度∇f(x)=0,梯度公式推导后如式8所示,由此定义最小二乘法的正规方程如式9所示:
式9 最小二乘法正规方程
分析:分析式9中的正规方程,其等价于∇f(x)=0,f(x)=,且最小二乘法问题所有解都满足正规方程。如果A的列线性无关,则A^TA为非奇异矩阵,此时正规方程(原问题)有唯一解。
对于正规方程的求解一般有三种方法,分别为直接求解正规方程组求解、通过Gram矩阵求解与QR分解求解,后两种方法实现流程详解如下:
4.1 通过Gram矩阵求解正规方程
通过Gram矩阵求解正规方程一般流程如表3所示:

Tips:经过四舍五入之后,Gram矩阵为奇异矩阵。
4.2 通过QR分解求解正规方程
方法②比方法①更稳定,因为它避免构造Gram矩阵,通过QR分解求解正规方程一般流程如表4所示:

5.编程实践
根据实验任务1)的要求,本部分将编程实践通过最小二乘法的正规方程,求出给定数据优化模型的准确解。
5.1 QR分解
对实验给定矩阵A与向量b进行导入,并对A进行QR分解(Householder),算法流程如表5所示:

在代码实现上,可使用matlab库函数[Q,R] = qr(A)使用Householder进行QR分解,用法解析可见:QR 分解 - MATLAB qr - MathWorks 中国,也可自己构建QR分解函数,分解与稳定性分析代码可见:最优化方法——QR分解_@李忆如的博客-CSDN博客
5.2 求最优解
在得到给定矩阵A分解出的Q、R矩阵(不同QR分解得到不同矩阵,需要转换)后,根据公式10对Q、R、b进行求最优解并编程实现(逆矩阵可用inv()函数求),最终得到最优解x_least并保存供后续对比,代码如下:
x_least=inv(R)*Q'*b; %精确解
五、梯度下降法
除了最小二乘法,梯度下降法也常用于最优化问题最优解的逼近,尤其是对于R^mxn列向量线性相关或n非常大的情况,本部分对于梯度下降法法的定义、数学模型化、目标求解推导、模型求解做详解。
1.定义
梯度下降法是一个一阶最优化算法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。即梯度下降法求解目标问题最优解的过程为:x1,x2,…,xk→x,其中xk是第k步迭代,期望更新xk+1,满足f(xk+1)









