🧡🧡实验内容🧡🧡
TSP问题是组合数学中一个古老而又困难的问题,也是一个典型的组合优化问题,现已归入NP完备问题类。NP问题用穷举法不能在有效时间内求解,所以只能使用启发式搜索。遗传算法是求解此类问题比较实用、有效的方法之一。下面给出30个城市的位置信息:
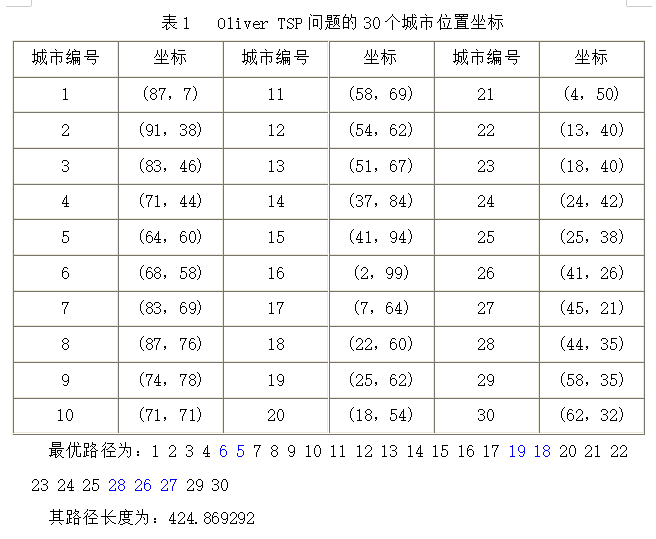
应用遗传算法和蚁群优化算法求解30/10个节点的TSP(旅行商问题)问题,求问题的最优解。
🧡🧡遗传算法求解🧡🧡
主要参数定义
染色体的定义:
每一条染色体定义为一条路线,其上的基因代表城市编号,例如:染色体:[5,1,2,3,4],,代表路径为5->1->2->3->4->5。
适应度的定义:
路径之间的距离和,是使得这个值最小,而本实验为方便轮盘赌根据适应度大小选择染色体,取路径距离和的负值,即在求解过程中保留适应度大的染色体。 例如:染色体:[5,1,2,3,4],,代表 min( len(5->1) + len(1->2) + len(2->3) + len(3->4) + len(4->5) )。
选择操作:
采用轮盘赌的选择方法,适应度大的更有机会被选择到。
交叉操作:
为确保每个城市只走一次,因此染色体交叉前后,其上面的基因都应该满足含有城市编号1~N(N为城市个数),且各个基因不重复,因此采用如下交叉方式

变异操作:
对染色体进行两点变异,也可逆转变异(根据变异前后最优适应度对比,决定是否采用变异)
交叉率和变异率:
每一根染色体都有可能进行交叉和突变,取决于交叉率和突变率。
种群规模(染色体数量):
大的种群可以保证每一代里拥有的染色体更多,交叉和突变得到的新染色体更多,有助于跳出局部最优解,尽早获得全局最优解。
代码
clear all;
close all;
clc;
%% 初始化参数
% 生成城市坐标
C=[
87,7;
91,38;
83,46;
71,44;
64,60;
68,58;
83,69;
87,76;
74,78;
71,71;
58,69;
54,62;
51,67;
37,84;
41,94;
2,99;
7,64;
22,60;
25,62;
18,54;
4,50;
13,40;
18,40;
24,42;
25,38;
41,26;
45,21;
44,35;
58,35;
62,32;
];
% C=C(1:10,:); %取前十个城市
N=size(C,1); %TSP问题的规模,即城市数目 (31个),染色体的基因数目
D=zeros(N); %任意两个城市距离间隔矩阵
%% 求任意两个城市距离间隔矩阵
for i=1:N
for j=1:N
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
end
end
NP=200; % 种群数目 染色体条数
G=1000; % 遗传代数
pc=0.8; % 交叉概率
pm=0.5; % 变异概率
f=zeros(NP,N); % 用于存储种群 每一行代表一条染色体
F = []; % 种群更新中间存储
for i=1:NP
f(i,:)=randperm(N); % 随机生成初始种群
end
best_f = f(1,:); % 存储最优种群
len=zeros(NP,1); % obj:走完所有城市总共要走的路径长度
fitness = zeros(NP,1); % 归一化后的len
gen = 0;
%% 遗传算法循环
tic;
while gen=rand % rand = 0-1的某个数
% nn = nn+1;
% F(nn,:)=f(i,:);
% end
% end
% 轮盘赌选择
nn=75;
F=zeros(nn,N);
total_fitness = sum(fitness);
selection_prob = fitness / total_fitness;
cumulative_prob = cumsum(selection_prob);
r = rand(nn, 1); % 生成一组随机数
for i=1:nn
select=find(cumulative_prob>=r(i)); % 下标数组
select_idx=select(1); % 事件序号
F(i,:)=f(select_idx,:);
end
[aa,bb] = size(F); % aa 








