WWDC 2024
2024 年的 WWDC 于昨晚凌晨一点召开。
总的来说,各系统(尤其是主设备系统 MacOs、iOS 和 iPadOS)升级幅度巨大,但仍有一些新功能比较鸡肋(至少在发布会上看上去是)。
篇幅有限,我们只挑有意思的来看一下。
如果这些功能都不足以吸引你升级,那还是留在现在的系统养老吧。
iOS 18
UI 的全面自定义。
支持从锁屏界面,到控制中心,再到主屏幕的全面自定义(颜色 + 布局)。

不过官方提供的这些 demo 也太丑了。
一句话:会是部分用户的需要,虽然官方提供的 demo 很丑,但用户想象是无限的,开放客制化或许会更好,至少消除了一部分的审美疲劳。
iPadOS 18
计算器 App 在 iPad 上市的 14 年后,终于上线。
除了是 iOS 版计算器的 Plus 版以外,还支持「计算历史」和「数学笔记」功能。
其中「数学笔记」功能支持识别手写的数据公式,并按照你的笔迹直接显示结果。
 白色字迹为手写内容,橘色字体为生成内容
白色字迹为手写内容,橘色字体为生成内容
 支持实时更新结果
支持实时更新结果
除了这些基础玩法以外,甚至支持图形、曲率、微积分和其他物理公式计算,也自动化创建图表。

一句话总结:少部分学生,有了前所未有的,升级到 iPad Pro 的正当理由。
MacOS
iPhone 可以投屏到 Mac 上了,并支持通过 Mac 上的键鼠来操作 iPhone,还支持双向的数据互通。
好功能,但什么生产力也就图一乐,这主要还是 Apple 为了让各位摸鱼更加方便。
一句话总结:支持打工人在 Mac 上玩手机啦。
AI - Apple Intelligence(苹果智能)
重新定义 AI。
首先,是对 Siri 进行了史诗级的更新。
现在的 Siri 除了定闹钟比较好使,对于其他的用户个性化指令,统统都是采用网页搜索的解决方案,而且搜得还不太好。
全新的 Siri 则接入打通了用户数据(邮件、电话、短信 等等),未来你问 Siri「我接下来有什么安排」这样的问题,她将不再是仅仅将「待办事项」中的设定给你念一遍,而是可能会把你「在邮件中答应参加的会议」或在「某个 App 预定好的机票行程」都给你列出来。
然后,是系统级别的「文生文」和「文生图」功能,支持指定情绪的文本重写润色、提取摘要,生成表情图片等等。
最后,还有图片一键修图功能,支持涂抹掉路人和杂物等操作。
值得注意的是,Apple 要实现这些效果,背后必然是要让 AI 读取了大量用户数据才能做到,但 Apple 仍然强调了背后的隐私安全性。
简单来说,这些 AI 操作会根据算力要求不同,采取不同的执行策略。
例如简单的指令,会优先在本地大模型执行,复杂的指令要求,可能会通过云端大模型来执行,而这个云端大模型的背后,目前来看大概率是 ChatGPT-4o 这一独立方案。
不管这里面是否有戳到你的亮点,但这确实是过去五年,苹果系统改动最大的一次 WWDC 了。
对此,你怎么看?
...
回归主线。
来一道和「腾讯校招」相关的算法原题。
题目描述
平台:LeetCode
题号:782
一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能任意交换两列或是两行的位置。
返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换,输出 -1。
“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
示例 1: 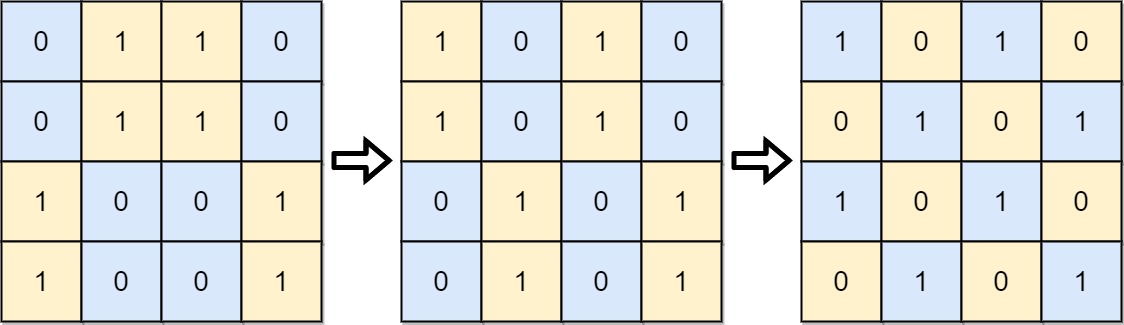
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下,从左到右:
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。
示例 2: 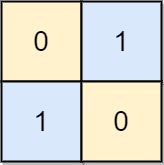
输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘,也是合法的棋盘.
示例 3: 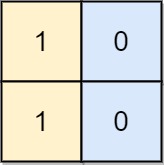
输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。
提示:
-
board[i][j] 将只包含
0或
1
构造分析
数据范围具有一定的迷惑性,但其并不是一个棋盘搜索问题。
我们需要考虑何种情况下无解,以及有解情况的最小步数。
在给定棋盘大小 n 的前提下,所能构造的合法棋盘只有两种情况:首个格子为 0 或首个格子为 1,即问题转化为能否构造出合法棋盘,以及构造哪种合法棋盘所用步数更小。
同时,「交换行和交换列均不会影响行的种类数量和列的种类数量」,因此我们可以得到第一个判断无解的条件:若起始棋盘的行 / 列种类数不为 2,必然无法构造出合法棋盘。
假设起始的行分别为 r1 和 r2,起始的列分别为 c1 和 c2。
不难发现第二性质:「若能构成合法棋盘,r1 和 r2 中 0 和 1 的数量必然相等,c1 和 c2 中的 0 和 1 的数量必然相等」。
同时由于交换行和交换列具有对称性和独立性,我们可以先使用「交换列」来进行分析,交换列不会导致行种类发生变化,但会导致行的数值分布发生变化。
因此第二性质可拓展为:「因为 r1 和 r2 对称位置必然不同,c1 和 c2 对称位置必然不同,即两者异或结果为必然为 ,即为 mask = (1









