大模型技术论文不断,每个月总会新增上千篇。本专栏精选论文重点解读,主题还是围绕着行业实践和工程量产。若在阅读过程中有些知识点存在盲区,可以回到如何优雅的谈论大模型重新阅读。另外斯坦福2024人工智能报告解读为通识性读物。若对于如果构建生成级别的AI架构则可以关注AI架构设计。技术宅麻烦死磕LLM背后的基础模型。当然最重要的是订阅跟随“鲁班模锤”。
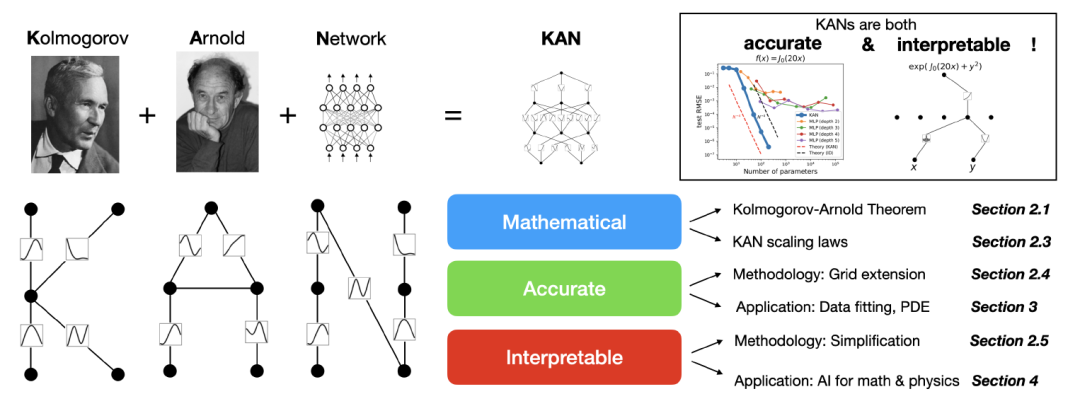
记得在《重新审视神经网络》这篇文章中提及,任何人都可以构建自己心目中的神经网络。就当小编还在准备Mamba时,说时迟,那时快。在不断发展的AI领域,五一劳动节期间一种新的架构正在掀起波澜,来自麻省理工学院的创新框架被称为柯尔莫哥洛夫-阿诺德网络(KAN),准备以其独特的方法改变传统模型。
KAN概览
这种新型的网络架构的核心思想基于由柯尔莫哥洛夫-阿诺德表示定理,它被寄予期望能够替代多层感知器。MLP 在节点(“神经单元”)上具有固定的激活函数,而 KAN 在边上(“权重”)具有可学习的激活函数。KAN根本没有线性权重—每个权重参数都被参数化为一元的spline function。
大白话的意思就是:KAN中的每个激活函数不是在每个节点,而是在每条边上。由一个一元函数(univariate function)组成,这些函数本身也是参数。意味着函数即参数,每个权重参数不再是一个单一的数值,而是一个函数。
spline,a continuous curve constructed so as to pass through a given set of points and have a certain number of continuous derivatives.大致的意思就是spline是一条连续的曲线,这条曲线能够穿过给点的数据点,且拥有特定数目的连续导数
具体什么意思,不要着急慢慢来。先来看看KAN相对于MLP的优点:
-
这种简单的变化使得KAN在准确性和可解释性方面优于 MLP。
-
从理论上和经验上来说,KAN比MLP拥有更快的神经尺度法则。
-
KAN 可以直观地可视化,并且可以轻松地与人类用户交互。
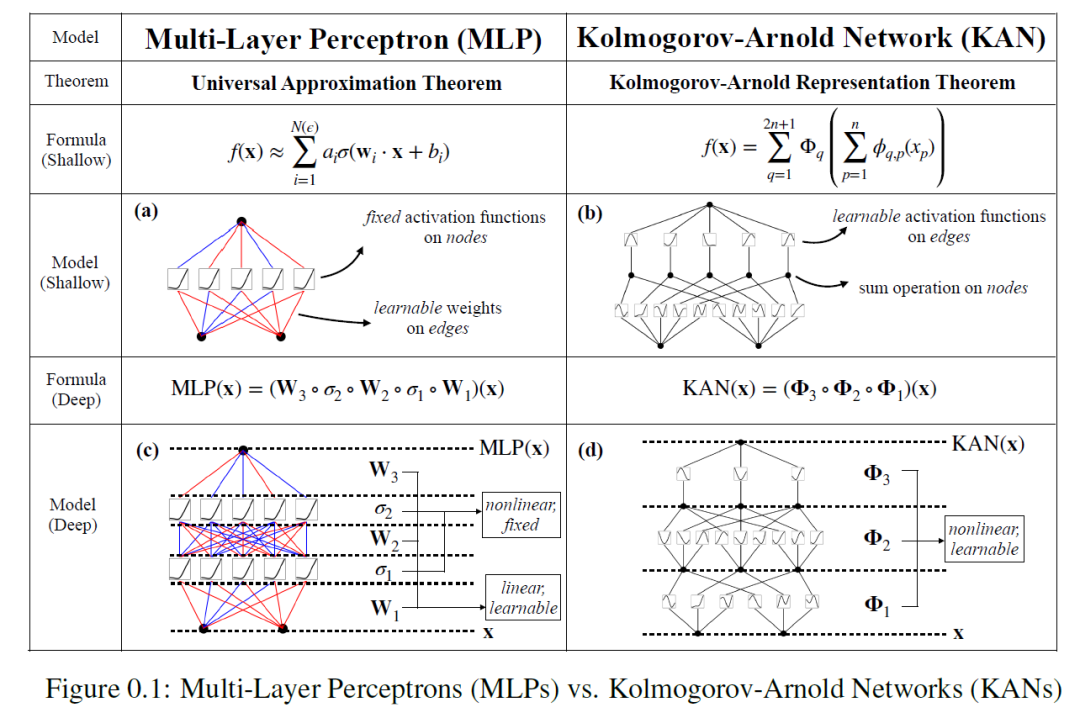
上图为两者之间的对比,最大的区别在于KAN学习的对象是边的激活函数,而每个节点仅仅做数值累加,KAN的多层累加有点函数套娃的意思。传统的激活函数是什么,可以回到初心去看看。
柯尔莫哥洛夫-阿诺德表示定理

这个定理是KAN的基石,用大白话文讲就是任何一个函数都可以转化为由单个变量的函数再套一层单变量的函数。
为了让大家更好的理解,举个一元二次方程的例子。相信大部分的同学都能写出来根的公式。而一元三次方程的根其实也是可以表示为a,b,c,d的函数。

那么一元四次,五次,六次呢,是不是更加复杂,关键是还能写得出来么。因此这个定理的贡献在于将高维函数简化成多项式数量的一维函数的组合。
为了让大家更好的理解,细究下这个定理的历史。故事来至希尔伯特的23个问题:大致的背景是德国数学家大卫·希尔伯特于1900年在巴黎举行的第二届国际数学家大会上作了题为《数学问题》的演讲,所提出23道最重要的数学问题。其中的第十三问题,希尔伯特希望数学界能够证明:x7+ax3+bx2+cx+1=0这个方程式的七个解,若表成系数为a,b,c的函数,则此函数无法简化成两个变数的函数。
后续柯尔莫哥洛夫证明每个有多个变元的函数可用有限个三变元函数构作。阿诺尔德按这个结果继续研究证明两个变元已足够。之后阿诺尔德和日本数学家志村五郎发表了论文(Superposition of algebraic functions (1976), in Mathematical Developments Arising From Hilbert's Problems)。
这些结果后来被进一步发展,推导出人工神经网络中的通用近似定理,指人工神经网络能近似任意连续函数。
KAN架构
先回到KA定理的公式:
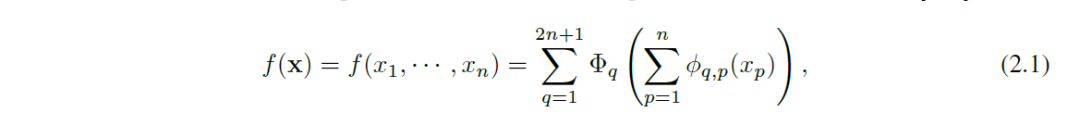
聪明的读者一定会发现,要是将这个做成神经网络,是不是只有两层非线性和一个隐藏层(2n+1),因为函数只套了一次。对的!加上一维函数可能是非光滑的,甚至是分形的(fractal),在实践无法学习。
这个函数其实看起来复杂,理解却是不难。第一层输入数目为n,举个例子,X1自身对应着2n+1个内圈函数Θq,1 (q=0...2n+1)。所以一共有n*(n+1)个内圈函数,将Θ1,1 , Θ1,2 ,Θ1,3 ,Θ1,4 , ... ,Θ1,n进行累加输出,一共输出2n+1个数值。第二层将2n+1个累加数值输入外圈函数Φ,得到1个输出。所以传统的KA是两层的,n->2n+1->1。
然而这次MIT做了技术突破,它们扩展了KA,提出了KAN架构。KAN架构的好处在于保留函数即参数的内核之外,将两层约束扩展到任意可以堆叠的网络结构。
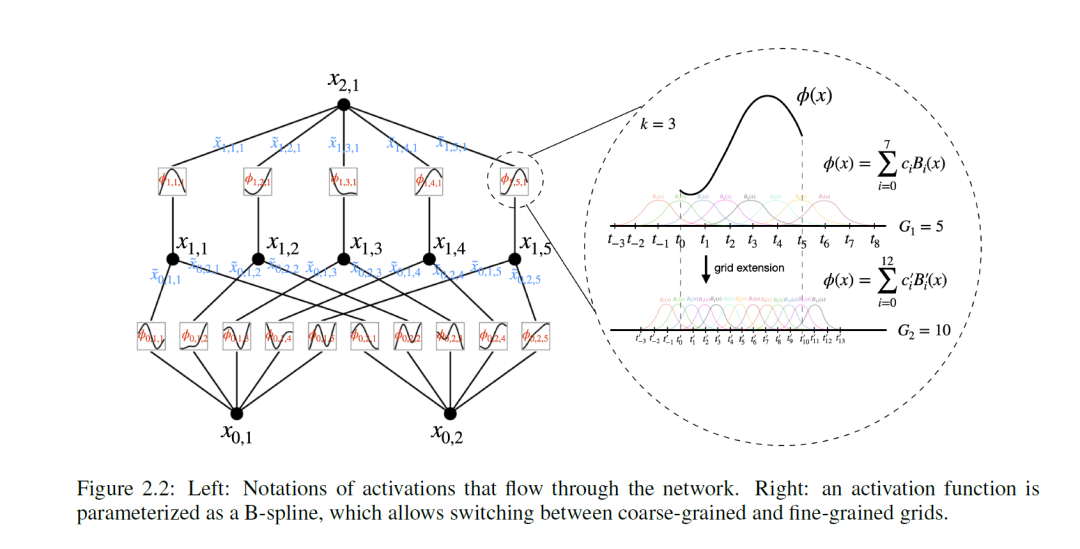
KAN的网络结构可以由[n0, n1, · · · , nL]这个整形数组来表达,每个数值代表着每一层的节点个数(节点执行累加的动作)。下图为中间层,任何一层输入,假定这个数组为[5,4,1],那么最早一层就是4*5的函数矩阵,在往下就是1*4的矩阵,最终输出为1个数值。想想为什么?不熟悉矩阵的同学可以温习下这篇文章。
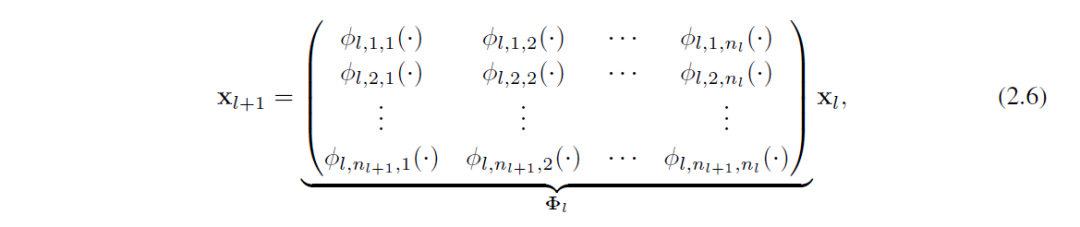
最终KAN网络的运作模式如下:从输入不断经过函数矩阵的变化达到最终的数值。2.7比较形象,2.8对于数学比较友好。
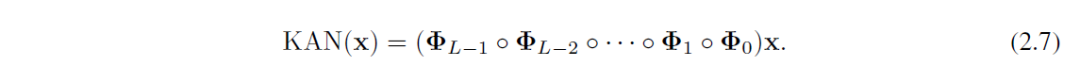
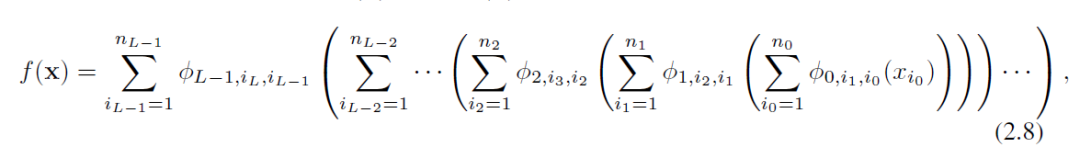
激活函数
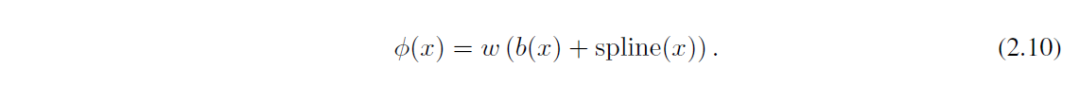
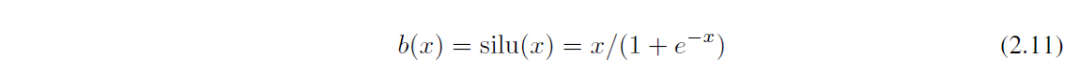
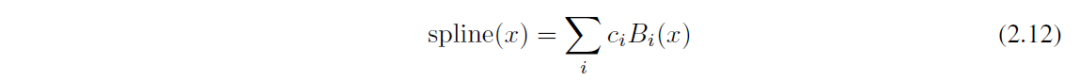
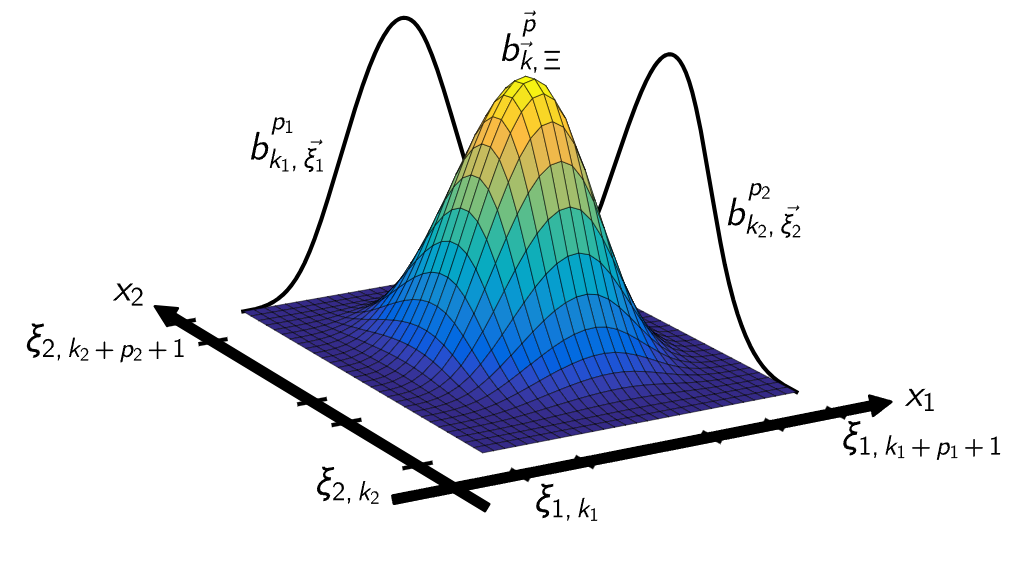
激活函数的长相如2.10所示,它由残差函数和Spline函数组合而成。w为权重,虽然它有点多余,毕竟可以被这两个函数吸收掉,但是可以来控制整个激活数值的缩放。2.11展示了残差函数。而Spline函数则是由B-splines构成。数学小白可以跳过B-splines函数,它其实就是分段连续的多项式曲线。
它有两个重要参数:节点和次数。数值域被细分成节点划分而成的多个区间。如何理解上面的公式在这里不重要,最重要的是它是一种构造曲线的方式。如此通过学习,校正激活函数以便于获得期望的输入和输出。
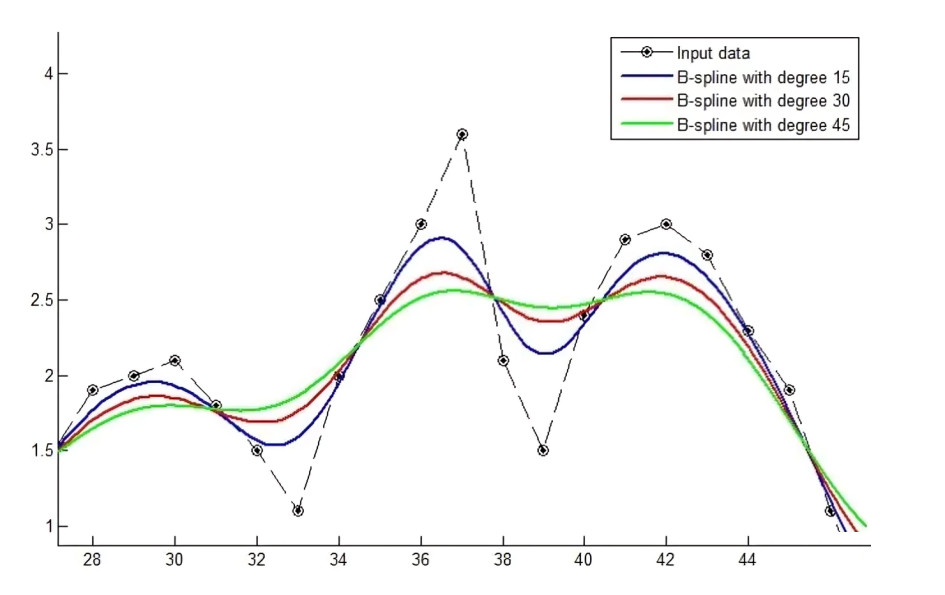
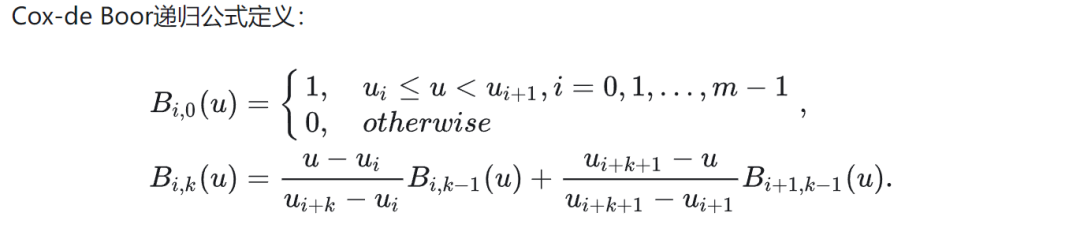
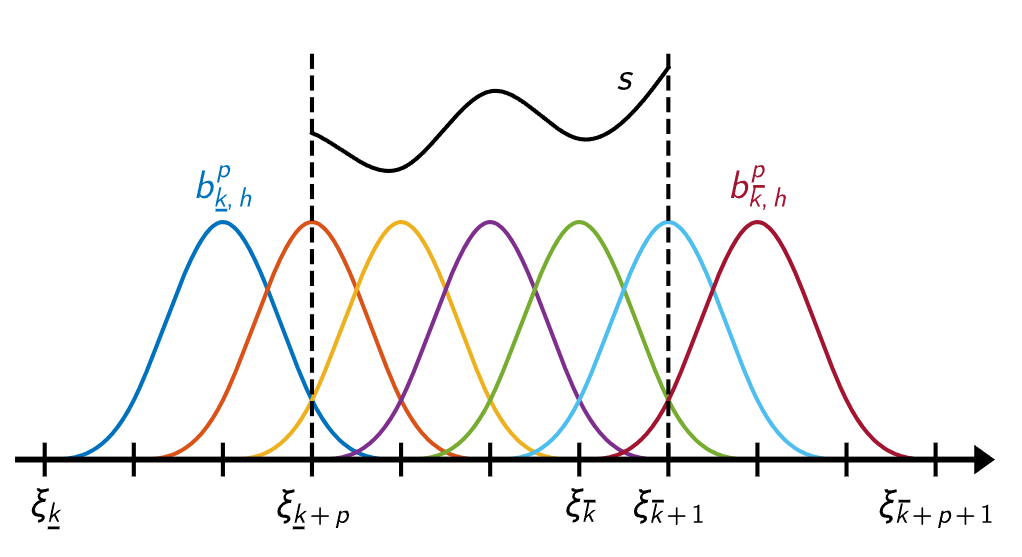
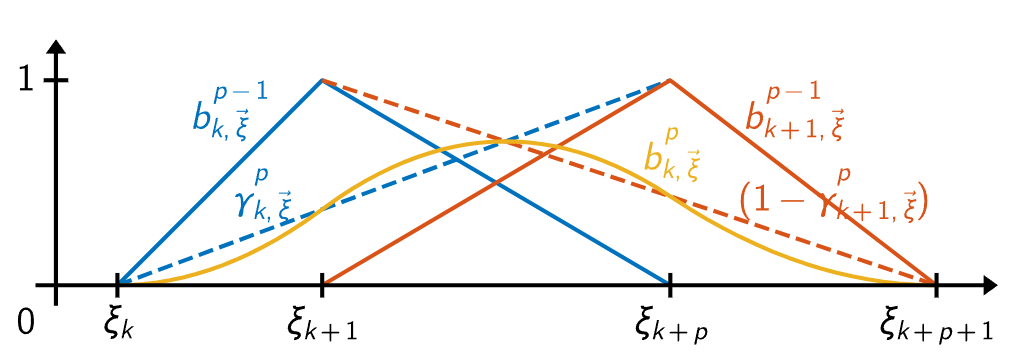
B-splines是一个分段连续的多项式曲线,它的参数域通过节点(knots)来表示,每两个节点之间是参数域的一段,比如一个B样条的参数域可以表示为:[𝑢0,𝑢1,𝑢2,𝑢3,𝑢4,𝑢5,𝑢6,𝑢7,𝑢8] ,一共9个节点;参数域分为8段:[𝑢0,𝑢1],[𝑢1,𝑢2],[𝑢2,𝑢3],[𝑢3,𝑢4],[𝑢4,𝑢5],...,[𝑢7,𝑢8] 。下面4幅图较为直观,可以通过不同的基函数构造出下面的曲线:
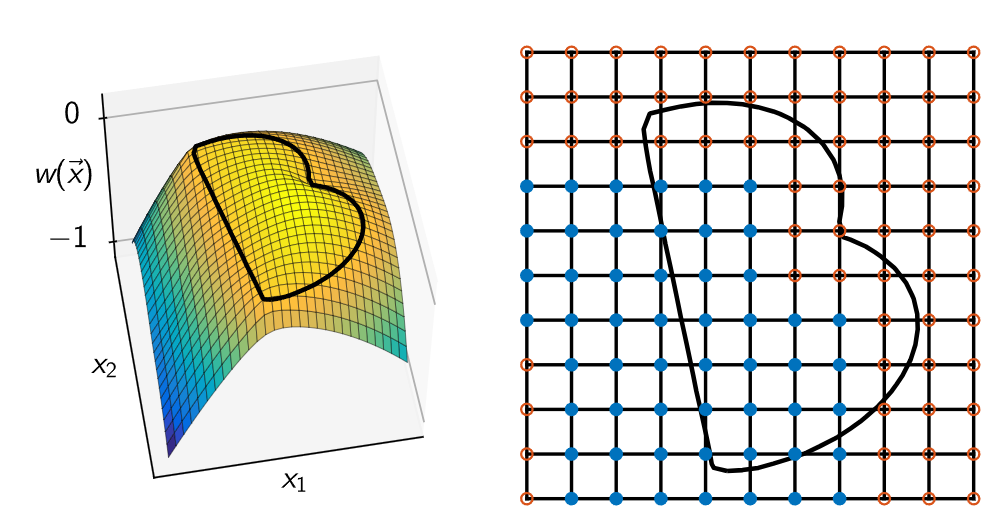
整体性能
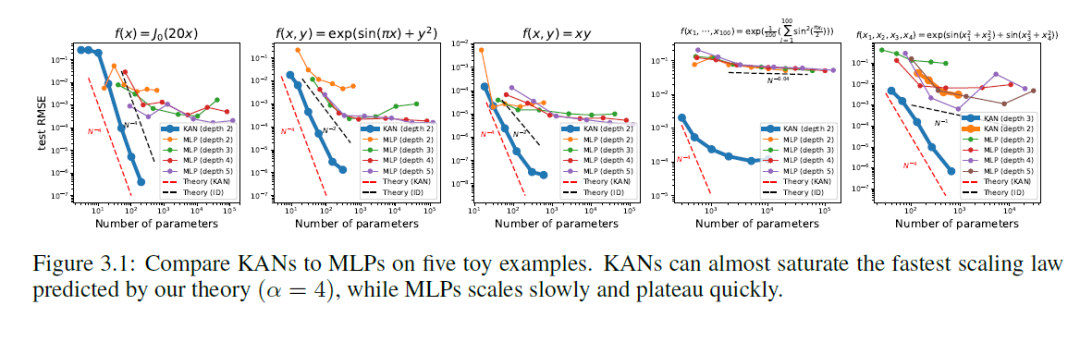
KAN的训练过程不在本文描述,它需要一定的技术背景,后续会另开专题详细的解释。为了可视化,研究人员设计一种交互式的监督学习,通过初训练,剪枝,然后设定一些比较常见的函数,最终再次训练参数(affine parameter)进而得到结果。事实上,它在已知函数表达式和未知函数表达式上的模拟都超过MLP。
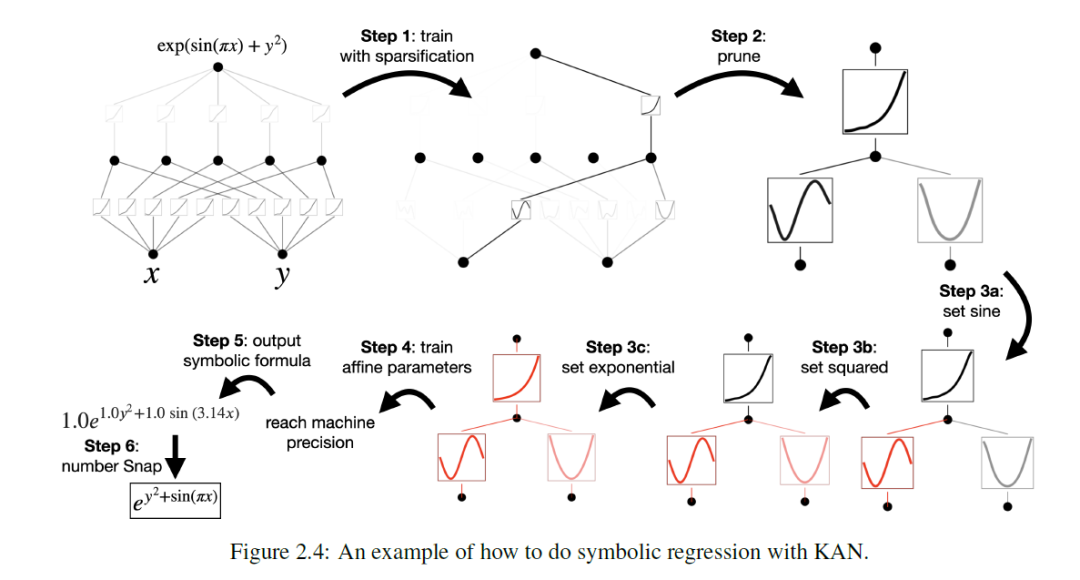
下图为五个函数,分别采用的KAN网络模拟,最多不会超过4层。最后一张图列出了它们和mlp对比,横轴为参数。