从零入门人工智能相关文档
从零入门人工智能之机器学习
- 一、机器学习之线性回归
- 1.机器学习介绍
- 2.线性回归
- 3.线性回归实战
- 4.python调用sklearn实现线性回归
- 二、机器学习之逻辑回归
- 1.分类
- 2.逻辑回归
- 3.实战(一):考试通过预测
- 4.实战(二):芯片质量预测
- 三、机器学习之聚类
- 1.无监督学习
- 2.KMeans、KNN、Mean-shift
- 3.实战(一):2D数据类别划分
- 4. 实战(二)
- 四、机器学习其他常用技术
- 1.决策树(Dicesion Tree)
- 2.异常检测(Anomaly Detection)
- 3.主成分分析(PCA)
- 4.实战(一):决策树实现iris数据集分类
- 5.实战(二):异常数据检测
- 6.实战(三):PCA降维后实现iris数据集分类
- 五、模型评价与优化
- 1.过拟合与欠拟合
- 2.数据分离与混淆矩阵
- 3.模型优化
- 4.实战(一):酶活性预测
- 5.实战(二):质量好坏预测
一、机器学习之线性回归
1.机器学习介绍
- 从数据中寻找规律、建立关系,根据建立的关系去解决问题的方法。
从数据中学习并且实现自我优化与升级
- 机器学习的类别:
- 监督学习–训练数据包括正确的结果,可应用于人脸识别、语音翻译、医学诊断。
- 无监督学习–训练数据不包括正确的结果,可应用于新闻聚类。
- 半监督学习–训练数据包括少量正确的结果
- 强化学习–根据每次结果收获的奖惩进行学习,实现优化,可应用于AlphaGO。
2.线性回归
- 根据数据,确定两种或两种以上变量间相互依赖的定量关系
函数表达式:

3.线性回归实战
scikit-learn是基于python的机器学习工具包,通过pandas、Numpy、Matplotlib等python数值计算的库实现高效的算法应用。
实战任务:
基于generated_data.csv数据,建立线性回归模型,预测x=3.5对应对的y值,评估模型表现。
#load the data import pandas as pd data = pd.read_csv('generated_data.csv') #data 赋值 x = data.loc[:,'x'] y = data['y'] print(type(x),x.head())
#visualize the data from matplotlib import pyplot as plt plt.figure(figsize=(4,4)) plt.scatter(x,y) plt.show()
使用sclearn时,需要导包
再黑框中输入 pip install scikit-learn -i https://pypi.tuna.tsinghua.edu.cn/simple
#set up a linear regression model from sklearn.linear_model import LinearRegression lr_model = LinearRegression() #将x y从一维转为二维 import numpy as np x = np.array(x).reshape(-1,1) y = np.array(y).reshape(-1,1) #训练模型,确定参数 拟合 lr_model.fit(x,y)

#查看预测结果是否跟y吻合 y_predict = lr_model.predict(x) print(y_predict)

#查看3.5对应的y值 y_3= lr_model.predict([[3.5]]) print(y_3)

#查看系数a,截距b a = lr_model.coef_ b = lr_model.intercept_ print(a,b)

metrics提供了丰富多样的评价指标,可以根据实际任务类型和需求选择合适的度量来评估模型性能。
#求均方差(MSE),方差R方 from sklearn.metrics import mean_squared_error,r2_score MSE = mean_squared_error(y,y_predict) r2 = r2_score(y,y_predict) print(MSE,r2)

4.python调用sklearn实现线性回归
任务:
基于usa_housing_price.csv数据,建立线性回归模型,预测合理房价:
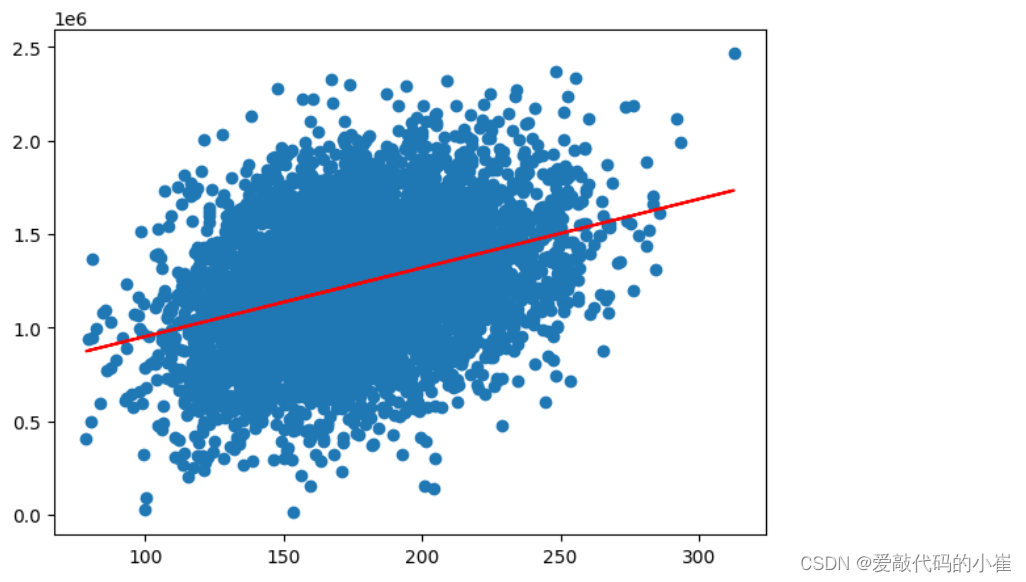
1. 以面积为输入变量建立单因子模型,评估模型表现,可视化线性回归预测结果
2. 以income、house age、numbers of rooms、population、area为输入变量,建立多因子模型,评估模型表现
3. 预测Income = 65000,House Age = 5,Number of Rooms = 5,Population = 30000,size = 200的合理房价
#load the data import pandas as pd data = pd.read_csv('usa_housing_price.csv') data.head()
from matplotlib import pyplot as plt plt.figure(figsize = (15,10)) fig1 = plt.subplot(231) plt.scatter(data['Avg. Area Income'],data['Price']) plt.title('Price vs Income') fig2 = plt.subplot(232) plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price']) plt.title('Price vs House Age') fig3 = plt.subplot(233) plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price']) plt.title('Price vs Rooms') fig4 = plt.subplot(234) plt.scatter(data['Area Population'],data['Price']) plt.title('Price vs Area Population') fig5 = plt.subplot(235) plt.scatter(data['size'],data['Price']) plt.title('Price vs size') plt.show()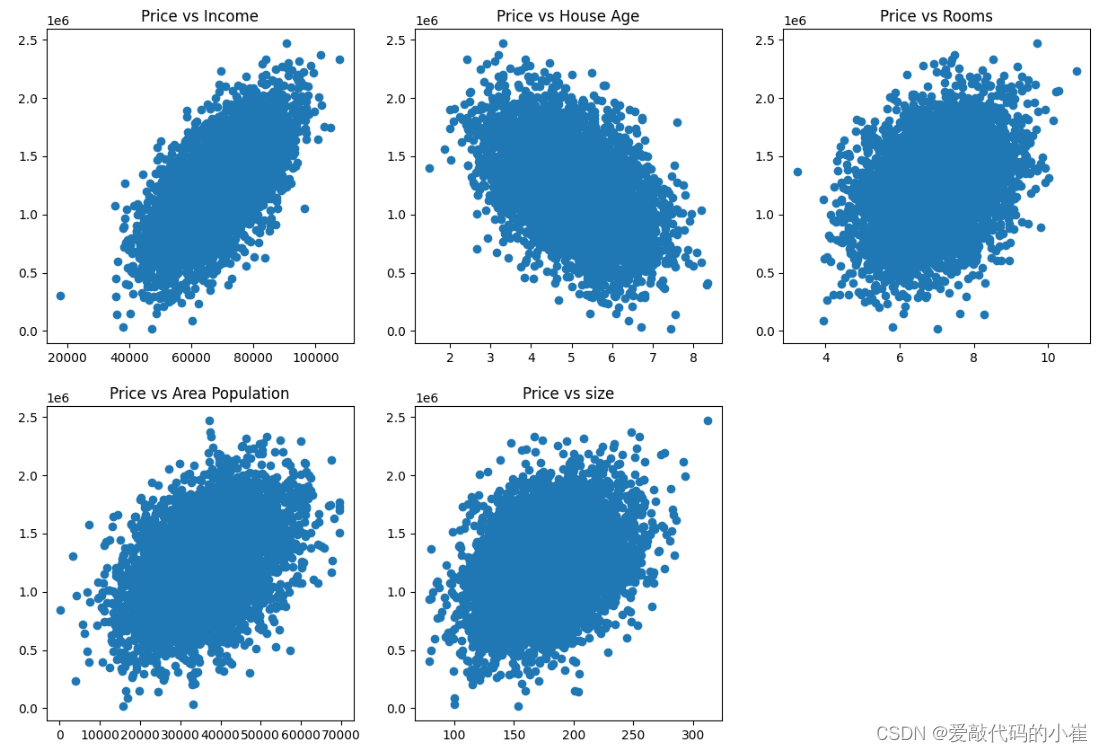
#define x and y import numpy as np x = data.loc[:,'size'] y = data.loc[:,'Price'] x = np.array(x).reshape(-1,1) y = np.array(y).reshape(-1,1) print(type(x),x,x.shape)
单因子模型
#set up the linear regression model from sklearn.linear_model import LinearRegression LR1 = LinearRegression() #train the model LR1.fit(x,y)

#calculate the price vs size y_predict_1 = LR1.predict(x) print(y_predict_1)

#evaluate the model from sklearn.metrics import mean_squared_error,r2_score MSE = mean_squared_error(y,y_predict_1) r2 = r2_score(y,y_predict_1) print(MSE,r2)

fig6 = plt.figure(figsize=(7,5)) plt.scatter(x,y) plt.plot(x,y_predict_1,'r') plt.show()
多因子模型
drop函数默认删除行,列需要加axis = 1
#define x_multi x_multi = data.drop(['Price'],axis = 1) print(x_multi.shape)

#set up linear model LR_multi = LinearRegression() #train the model LR_multi.fit(x_multi, y)

#make prediction y_multi_predict = LR_multi.predict(x_multi) print(y_multi_predict)

MSE_multi = mean_squared_error(y,y_multi_predict) r2_multi = r2_score(y,y_multi_predict) print(MSE_multi,r2_multi)

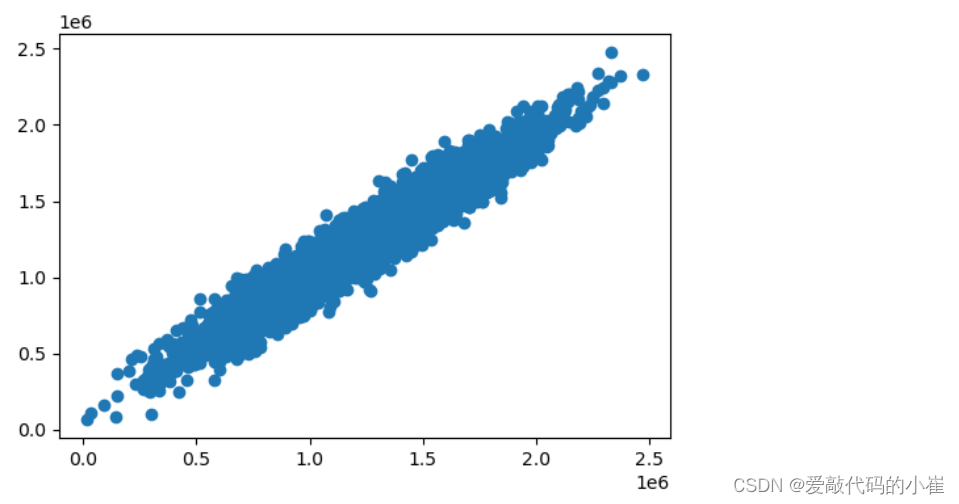
多因子无法看x和y的效果,只能查看y和y_multi_predict
fig7 = plt.figure(figsize = (6,4)) plt.scatter(y,y_multi_predict) plt.show()
x_test = [65000,5,5,30000,200] x_test = np.array(x_test).reshape(1,-1) print(x_test)

y_test_predict = LR_multi.predict(x_test) print(y_test_predict)

二、机器学习之逻辑回归
1.分类
根据已知样本的某些特征,判断一个新的样本属于哪种已知的样本类。
2.逻辑回归
用于解决分类问题的一种模型。根据数据特征或属性,计算其归属于某一类别的概率P(x),根据概率数值判断其所属类别。主要应用场景:二分类问题。
逻辑回归求解:
1. 根据训练样本,寻找类别边界;
p ( x ) = 1 1 + e − g ( x ) p(x) = {1 \over 1 + e^{-g(x)}} p(x)=1+e−g(x)1
g ( x ) = θ 0 + θ 1 X 1 + θ 2 X 2 + . . . . g(x) = \theta_0 + \theta_1X_1 + \theta_2X_2 + .... g(x)=θ0+θ1X1+θ2X2+....
根据训练样本确定参数 θ 0 θ 1 θ 2 \theta_0 \theta_1 \theta_2 θ0θ1θ2 。
- 逻辑回归求解,最小损失函数(J):
J i = { − l o g ( p ( x i ) ) , i f y i = 1 − l o g ( 1 − p ( x i ) ) , i f y i = 0 J_i = \begin{cases} -log(p(x_i)),\,\ if \,\ y_i = 1 \\ -log(1-p(x_i)), \,\ if \,\ y_i = 0 \end{cases} Ji={−log(p(xi)), if yi=1−log(1−p(xi)), if yi=0
J = 1 m ∑ i = 1 m J i = − 1 m [ ∑ i = 1 m ( J i l o g ( p ( x i ) ) + ( 1 − y i ) l o g ( 1 − p ( x i ) ) ) ] J = {1 \over m} \sum_{i=1}^mJ_i = -{1 \over m} [\sum_{i=1}^m (J_ilog(p(x_i)) +(1-y_i)log(1-p(x_i))) ] J=m1i=1∑mJi=−m1[i=1∑m(Jilog(p(xi))+(1−yi)log(1−p(xi)))]
3.实战(一):考试通过预测
任务:
1. 基于examdata.csv数据,建立逻辑回归模型,评估模型表现
2. 预测Exam1 = 75,Exam2 = 60时,该同学能否通过Exam3
3. 建立二阶边界函数,重复任务1、2
加载examdata.csv数据
#load the data import pandas as pd import numpy as np data = pd.read_csv('examdata.csv') data.head()
#visualize the data from matplotlib import pyplot as plt fig1 = plt.figure(figsize = (6,4)) plt.scatter(data['Exam1'],data['Exam2']) plt.title('Exam1-Exam2') plt.xlabel('Exam1') plt.ylabel('Exam2') plt.show()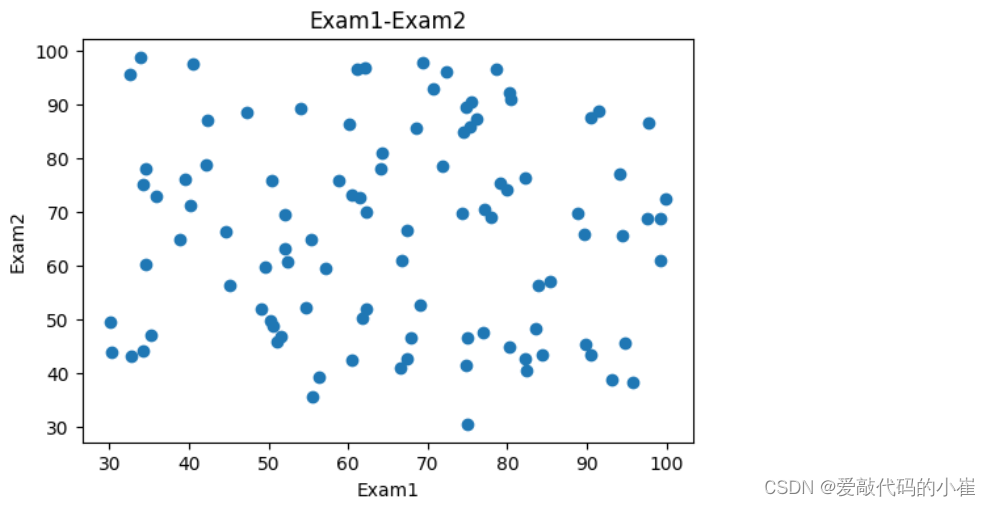
#add lable mask 添加标签 mask = data.loc[:,'Pass'] == 1 mask.head()
对添加标签后的数据进线可视化,legend()函数是用来在图形中显示图例名称的,可以帮助观察者区分不同的数据来源或类别
fig2 = plt.figure(figsize = (6,4)) passed = plt.scatter(data['Exam1'][mask],data['Exam2'][mask]) failed = plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask]) plt.title('Exam1-Exam2') plt.xlabel('Exam1') plt.ylabel('Exam2') plt.legend((passed,failed),('passed','failed')) plt.show()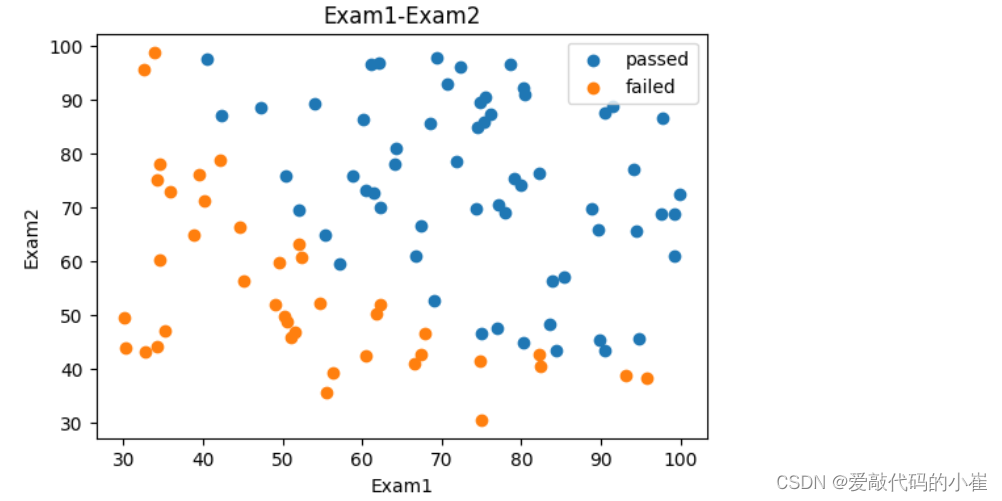
#define x y x = data.drop(['Pass'],axis = 1) y = data.loc[:,'Pass'] print(x.shape,y.shape)

#establish the model and train it from sklearn.linear_model import LogisticRegression LR = LogisticRegression() LR.fit(x,y)

#show the predicted result y_predict=LR.predict(x) print(y_predict)

#evaluate model accuracy from sklearn.metrics import accuracy_score accuracy_score_1 = accuracy_score(y,y_predict) print(accuracy_score_1)

#预测Exam1 = 75,Exam2 = 60时,该同学能否通过Exam3 #predict Exam1 = 75 and Exam2 = 60 x_test = [75,60] x_test = pd.array(y_test).reshape(1,-1) y_test_predict = LR.predict(y_test) print('passed' if y_test_predict == 1 else 'failed')
边界函数: θ 0 + θ 1 X 1 + θ 2 X 2 = 0 \theta_0 + \theta_1X_1 + \theta_2X_2 = 0 θ0+θ1X1+θ2X2=0
求解边界参数 θ 0 θ 1 θ 2 \theta_0 \theta_1 \theta_2 θ0θ1θ2,并根据公式求解 x 2 x_2 x2
theta0 = LR.intercept_ theta1,theta2 = LR.coef_[0][0],LR.coef_[0][1] print(theta0,theta1,theta2)

x1 = data.loc[:,'Exam1'] print(type(x1)) x2 = data.loc[:,'Exam2'] x2_new = -(theta0 + theta1*x1)/theta2

#对x1和预测结果x2_new进行可视化 fig3 = plt.figure(figsize = (6,4)) plt.plot(x1,x2_new) plt.show()
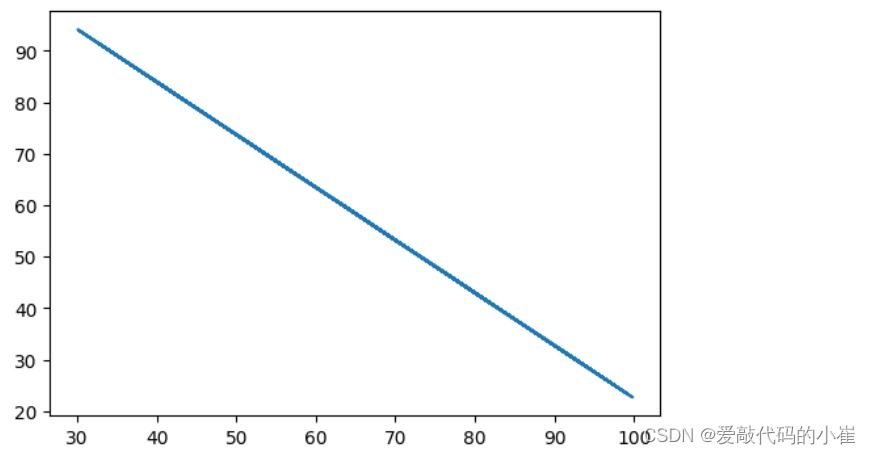
#Exam1—Exam2散点图与Exam1—预测边界数据可视化 fig4 = plt.figure(figsize = (7,5)) passed = plt.scatter(data['Exam1'][mask],data['Exam2'][mask]) failed = plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask]) plt.plot(x1,x2_new) plt.title('Exam1-Exam2') plt.xlabel('Exam1') plt.ylabel('Exam2') plt.legend((passed,failed),('passed','failed')) plt.show()
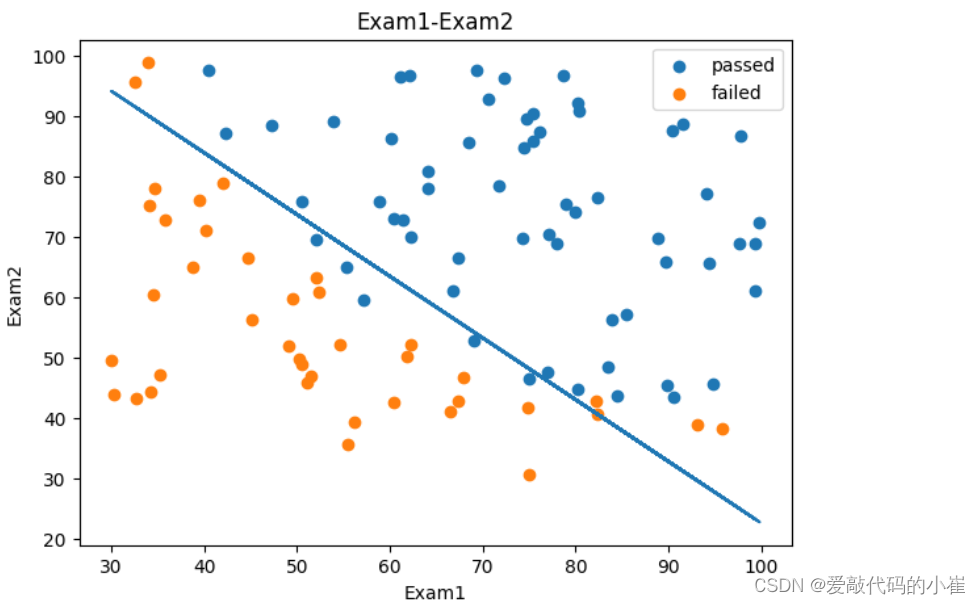
使用更加准确的二次函数进行预测
#create new data x1_2 = x1 * x1 x2_2 = x2 * x2 x1_x2 = x1 * x2 x_new = {'x1':x1, 'x2':x2, 'x1_2':x1_2, 'x2_2':x2_2, 'x1_x2':x1_x2} x_new = pd.DataFrame(x_new) x_new.head()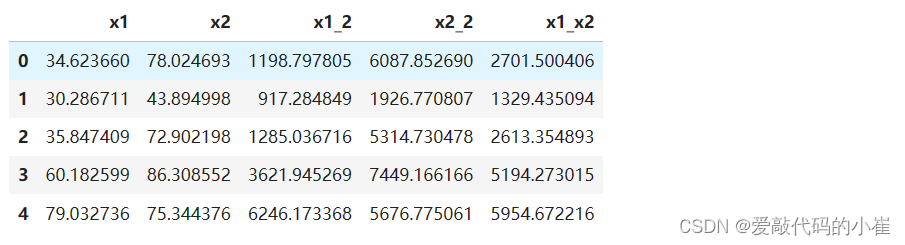
#establish new model and train LR2 = LogisticRegression() LR2.fit(x_new,y)

#evaulate the accuracy y2_predict=LR2.predict(x_new) accuracy_score_2 = accuracy_score(y,y2_predict) print(accuracy_score_2)
二阶边界函数: θ 0 + θ 1 X 1 + θ 2 X 2 + θ 3 x 1 2 + θ 4 x 2 2 + θ 5 x 1 x 2 = 0 \theta_0 + \theta_1X_1 + \theta_2X_2 + \theta_3x_1^2 + \theta_4x_2^2 + \theta_5x_1x_2= 0 θ0+θ1X1+θ2X2+θ3x12+θ4x22+θ5x1x2=0
a x 2 + b x + c = 0 : x 1 = ( − b + b 2 − 4 a c ) / 2 a : x 2 ( − b − b 2 − 4 a c ) / 2 a ax^2 + bx + c = 0 :\,\ x1 = (-b + \sqrt{b^2 - 4ac})/ 2a : \,\ x2 (-b - \sqrt{b^2 - 4ac})/ 2a ax2+bx+c=0: x1=(−b+b2−4ac )/2a: x2(−b−b2−4ac )/2a
θ 4 x 2 2 + ( θ 5 x 1 + θ 2 ) x 2 + ( θ 0 + θ 1 x 1 + θ 3 x 1 2 ) = 0 \theta_4x_2^2 + (\theta_5x_1 + \theta_2)x_2 + (\theta_0 + \theta_1x_1 + \theta_3x_1^2) = 0 θ4x22+(θ5x1+θ2)x2+(θ0+θ1x1+θ3x12)=0
求解函数参数 θ 0 θ 1 θ 2 θ 3 θ 4 θ 5 \theta_0 \theta_1 \theta_2 \theta_3 \theta_4 \theta_5 θ0θ1θ2θ3θ4θ5
x1_new = x1.sort_values() theta0 = LR2.intercept_ theta1,theta2,theta3,theta4,theta5 = LR2.coef_[0][0],LR2.coef_[0][1],LR2.coef_[0][2],LR2.coef_[0][3],LR2.coef_[0][4] print(theta0,theta1,theta2,theta3,theta4,theta5)

a = theta4 b = theta5*x1_new+theta2 c = theta0+theta1*x1_new+theta3*x1_new*x1_new x2_new_boundary = (-b + np.sqrt(b * b - 4 * a * c))/(2*a) x2_new_boundary.head()

fig5 = plt.figure(figsize = (6,4)) plt.plot(x1_new,x2_new_boundary) plt.show()
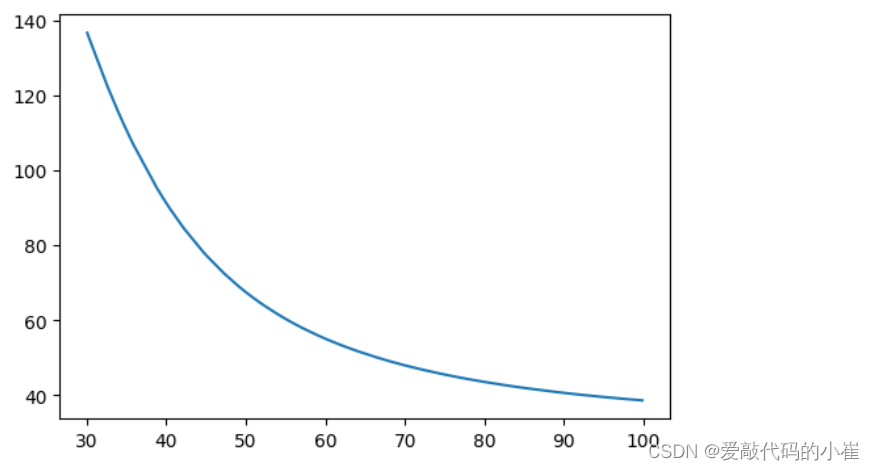
fig6 = plt.figure(figsize = (6,4)) passed = plt.scatter(data['Exam1'][mask],data['Exam2'][mask]) failed = plt.scatter(data['Exam1'][~mask],data['Exam2'][~mask]) plt.plot(x1_new,x2_new_boundary) plt.title('Exam1-Exam2') plt.xlabel('Exam1') plt.ylabel('Exam2') plt.legend((passed,failed),('passed','failed')) plt.show()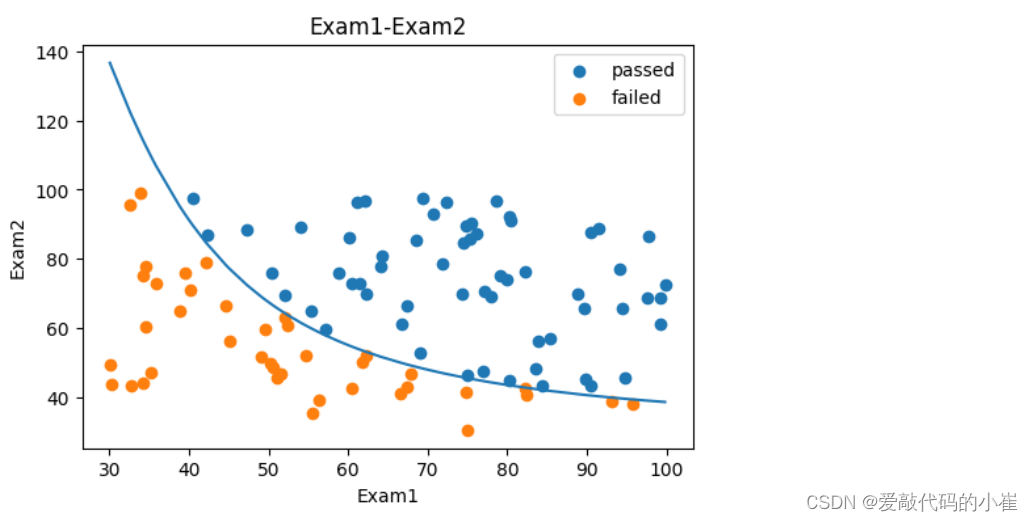
4.实战(二):芯片质量预测
任务:
1. 基于chip_test.csv数据,建立逻辑回归模型(二阶边界),评估模型表现
2. 以函数的方式求解边界曲线
3. 描绘出完整的决策边界曲线
#load the data import pandas as pd import numpy as np data = pd.read_csv('chip_test.csv') data.head()
#visualize the data from matplotlib import pyplot as plt fig1 = plt.figure(figsize = (6,4)) mask = data.loc[:,'pass'] == 1 passed = plt.scatter(data['test1'][mask],data['test2'][mask]) failed = plt.scatter(data['test1'][~mask],data['test2'][~mask]) plt.title('test1-test2') plt.xlabel('test1') plt.ylabel('test2') plt.legend((passed,failed),('passed','failed')) plt.show()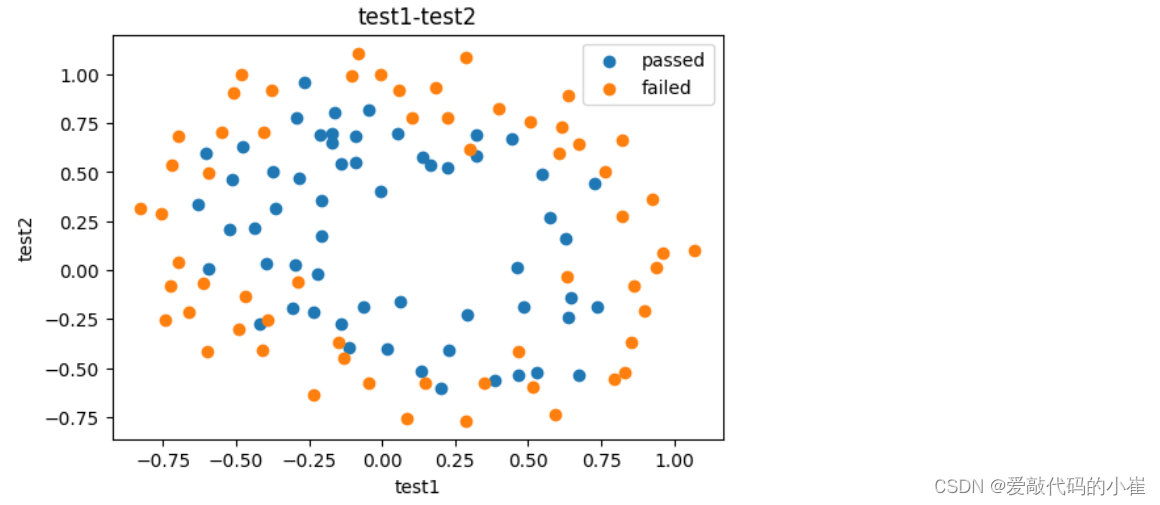
二阶边界函数: θ 0 + θ 1 X 1 + θ 2 X 2 + θ 3 x 1 2 + θ 4 x 2 2 + θ 5 x 1 x 2 = 0 二阶边界函数:\theta_0 + \theta_1X_1 + \theta_2X_2 + \theta_3x_1^2 + \theta_4x_2^2 + \theta_5x_1x_2= 0 二阶边界函数:θ0+θ1X1+θ2X2+θ3x12+θ4x22+θ5x1x2=0
#create new data x = data.drop(['pass'],axis = 1) y = data.loc[:,'pass'] x1 = data.loc[:,'test1'] x2 = data.loc[:,'test2'] x1_2 = x1 * x1 x2_2 = x2 * x2 x1_x2 = x1 * x2 x_new={'x1':x1,'x2':x2,'x1_2':x1_2,'x2_2':x2_2,'x1_x2':x1_x2} x_new=pd.DataFrame(x_new) x_new.head()
#establish the model and train from sklearn.linear_model import LogisticRegression LR=LogisticRegression() LR.fit(x_new,y)

#predict y_predict = LR.predict(x_new) print(y_predict)

#evaluate the accuracy_score from sklearn.metrics import accuracy_score accuracy = accuracy_score(y,y_predict) print(accuracy)

a x 2 + b x + c = 0 : x 1 = ( − b + b 2 − 4 a c ) / 2 a : x 2 ( − b − b 2 − 4 a c ) / 2 a ax^2 + bx + c = 0 :\,\ x1 = (-b + \sqrt{b^2 - 4ac})/ 2a : \,\ x2 (-b - \sqrt{b^2 - 4ac})/ 2a ax2+bx+c=0: x1=(−b+b2−4ac )/2a: x2(−b−b2−4ac )/2a
θ 4 x 2 2 + ( θ 5 x 1 + θ 2 ) x 2 + ( θ 0 + θ 1 x 1 + θ 3 x 1 2 ) = 0 \theta_4x_2^2 + (\theta_5x_1 + \theta_2)x_2 + (\theta_0 + \theta_1x_1 + \theta_3x_1^2) = 0 θ4x22+(θ5x1+θ2)x2+(θ0+θ1x1+θ3x12)=0
#decision boundary x1_new = x1.sort_values() theta0 = LR.intercept_ theta1,theta2,theta3,theta4,theta5=LR.coef_[0][0],LR.coef_[0][1],LR.coef_[0][2],LR.coef_[0][3],LR.coef_[0][4] a = theta4 b = theta5*x1_new+theta2 c = theta0+theta1*x1_new+theta3*x1_new*x1_new x2_new_boundary = (-b + np.sqrt(b * b - 4 * a * c))/(2*a) fig2 = plt.figure() passed = plt.scatter(data['test1'][mask],data['test2'][mask]) failed = plt.scatter(data['test1'][~mask],data['test2'][~mask]) plt.plot(x1_new,x2_new_boundary) plt.title('test1-test2') plt.xlabel('test1') plt.ylabel('test2') plt.legend((passed,failed),('passed','failed')) plt.show()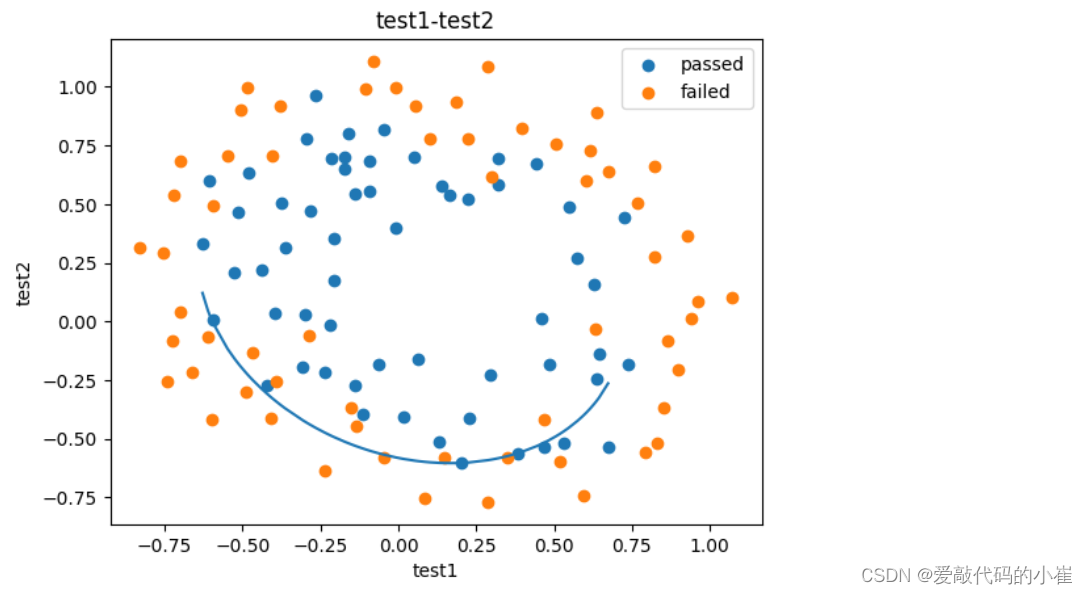
函数f(x)的返回值是一个元组(根1, 根2),元组是Python的一种序列类型,支持索引访问。对于一个包含n个元素的元组my_tuple,可以用my_tuple[i]来获取第i个元素(索引从0开始)。因此,在下面代码中:
- f(x)返回一个包含两个元素的元组,表示二次方程的两个根。
- 使用f(x)[0]和f(x)[1]分别访问这个元组的第0个和第1个元素,也就是两个根的值。
- 将这两个根分别追加到相应的列表x2_new_boundary1和x2_new_boundary2中,以收集所有输入x对应的二次方程根。
#define f(x) def f(x): a = theta4 b = theta5*x+theta2 c = theta0+theta1*x+theta3*x*x x2_new_boundary1 = (-b + np.sqrt(b * b - 4 * a * c))/(2*a) x2_new_boundary2 = (-b - np.sqrt(b * b - 4 * a * c))/(2*a) return x2_new_boundary1,x2_new_boundary2 x2_new_boundary1=[] x2_new_boundary2=[] for x in x1_new: x2_new_boundary1.append(f(x)[0]) #使用append()方法将元素添加到列表末尾 x2_new_boundary2.append(f(x)[1]) print(x2_new_boundary1)
fig3 = plt.figure() passed = plt.scatter(data['test1'][mask],data['test2'][mask]) failed = plt.scatter(data['test1'][~mask],data['test2'][~mask]) plt.plot(x1_new,x2_new_boundary1) plt.plot(x1_new,x2_new_boundary2) plt.title('test1-test2') plt.xlabel('test1') plt.ylabel('test2') plt.legend((passed,failed),('passed','failed')) plt.show()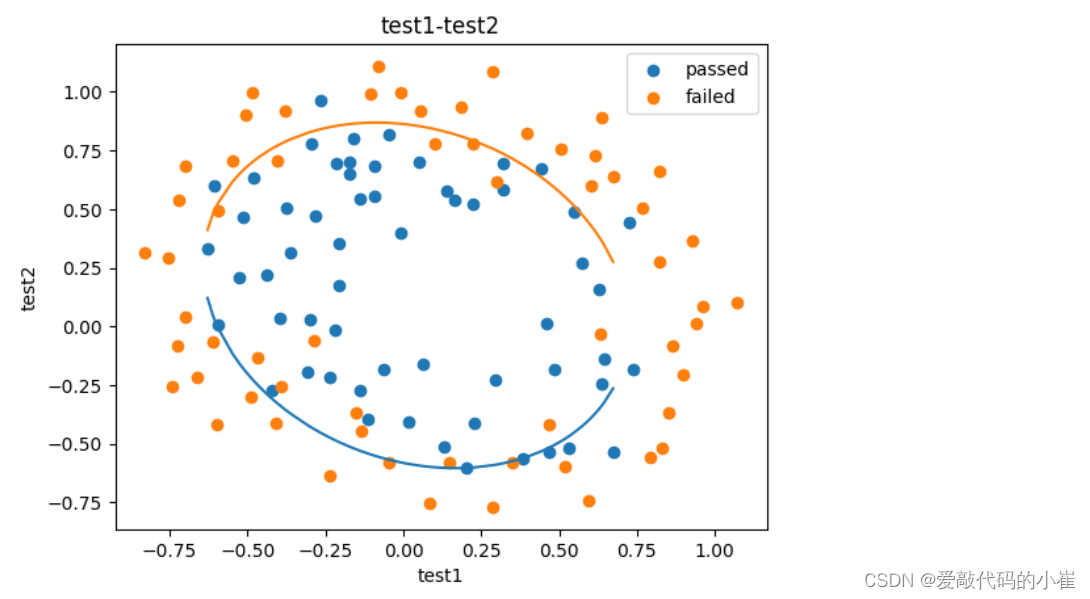
#创建x方向的密度集,解决画图过程中x轴数据分散导致图形不完整问题 x1_range = [-0.75 + x/10000 for x in range(0,19000)] x1_range = np.array(x1_range) x2_new_boundary1=[] x2_new_boundary2=[] for x in x1_range: x2_new_boundary1.append(f(x)[0]) x2_new_boundary2.append(f(x)[1]) fig4 = plt.figure() passed = plt.scatter(data['test1'][mask],data['test2'][mask]) failed = plt.scatter(data['test1'][~mask],data['test2'][~mask]) plt.plot(x1_range,x2_new_boundary1) plt.plot(x1_range,x2_new_boundary2) plt.title('test1-test2') plt.xlabel('test1') plt.ylabel('test2') plt.legend((passed,failed),('passed','failed')) plt.show()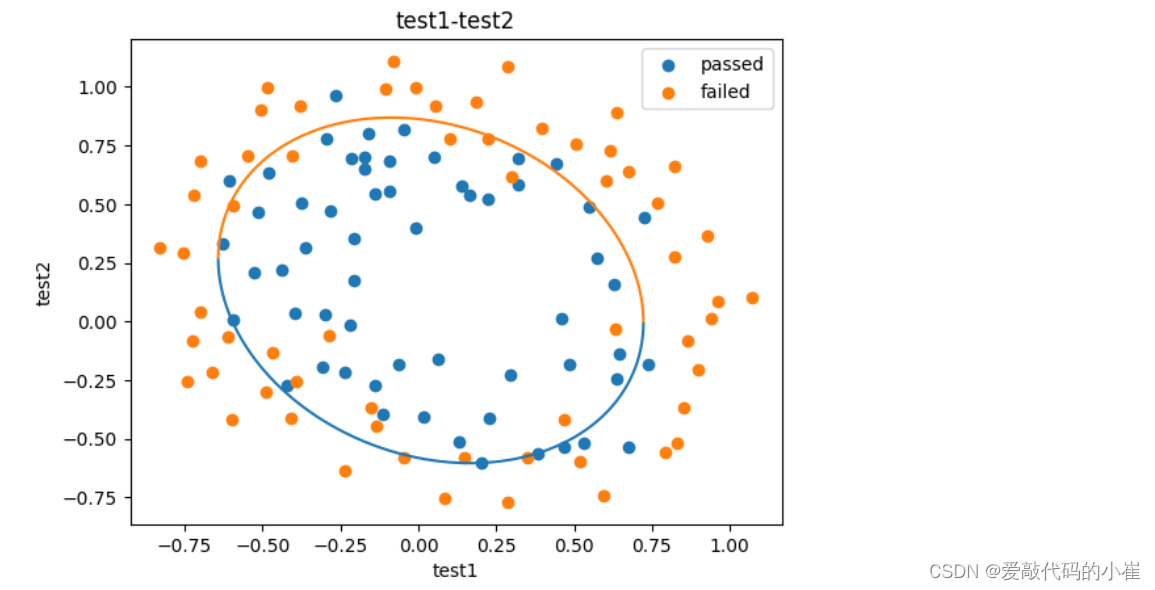
三、机器学习之聚类
1.无监督学习
- 概念:
机器学习的一种方法,没有给定事先标记的训练示例,自动对输入的数据进行分类和分群
- 优点:
- 算法不受监督信息的约束,可能考虑到新的信息
- 不需要标签数据,极大程度扩大数据样本
- 主要应用:
聚类分析、关联规则、维度缩减
2.KMeans、KNN、Mean-shift
聚类分析:又称群分析,根据对象某些属性的相似度,将其自动划分为不同的类别,例如:客户划分、新闻关联、基因聚类。
KMeans聚类(k均值聚类)
-
K-均值算法以空间中k个点为中心进行聚类,对最靠近他们的对象归类,是聚类算法中最为基础但也最为重要的算法
-
公式:
- 数据点与各簇中心点距离:dist( x i , u j t x_i,u_j^t xi,ujt)
- 根据距离归类: x i ∈ u n e a r e s t t x_i \in u_{nearest}^t xi∈unearestt
- 中心更新: u j t + 1 = 1 k ∑ x i ∈ s j ∞ ( x i ) u_j^{t+1} = {1 \over k} \sum_{x_i \in s_j}^\infty (x_i) ujt+1=k1xi∈sj∑∞(xi)
-
算法流程
- 选择聚类的个数k
- 确定聚类中心
- 根据点到聚类中心聚类确定各个点所属类别
- 根据各个类别数据更新聚类中心
- 重复以上不知直到收敛(中心点不再变化)
-
特点:
- 实现简单,收敛快
- 需要指定类别的数量
K近邻分类模型(KNN)
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分类到这个类中(监督学习)
Meanshift算法(均值漂移聚类)
-
一种基于密度梯度上升的聚类算法(沿着密度上升方向寻找聚类中心点)
-
算法流程:
- 随机选择未分类点作为中心点
- 找出离中心点距离在带宽之内的点,记作集合s
- 计算从中心点到集合s中每个元素的偏移向量M
- 中心点以向量M移动
- 重复步骤2-4直到收敛
- 重复1-5直到所有的点都被归类
- 分类:根据每个类,对每个点的访问频率,取访问频率最大的呢个类,作为当前点集的所属类
-
特点:
- 自动发现类别数量,不需要人工选择
- 需要选择区域半径
BDSCAN算法(基于密度的空间聚类算法)
-
- 基于区域点密度筛选有效数据
- 基于有效数据向周边扩张,知道没有新点加入
- 特点:
- 过滤噪音数据
- 不需要人为选择类别数量
- 数据密度不同时影响结果
3.实战(一):2D数据类别划分
任务:
1. 采用Kmeans算法实现2D数据自动聚类,预测V1=80,V2=60数据类别;
2. 计算预测准确率,完成结果矫正
3. 采用KNN、Meanshift算法,重复步骤1-2
采用Kmeans算法
#load the data import pandas as pd import numpy as np data = pd.read_csv('data.csv') data.head()无监督学习不需要标签(labels),这里的labels只是为了跟无监督式预测做一个对比
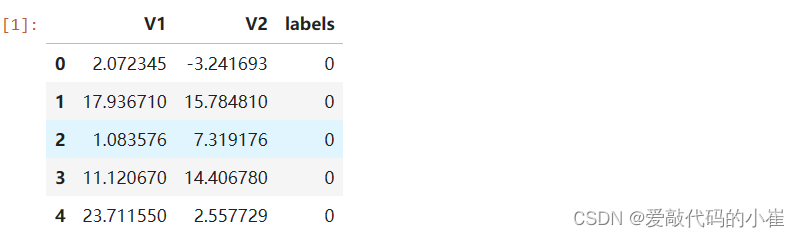
#define x and y x=data.drop(['labels'],axis=1) y=data.loc[:,'labels'] x.head()

#visualize the data from matplotlib import pyplot as plt fig=plt.figure(figsize=(12,8)) fig1=plt.subplot(221) plt.scatter(data.loc[:,'V1'],data.loc[:,'V2']) plt.title('un-label data') plt.xlabel('V1') plt.ylabel('V2') fig2=plt.subplot(222) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()无标签数据绘图与有标签数据绘图做对比
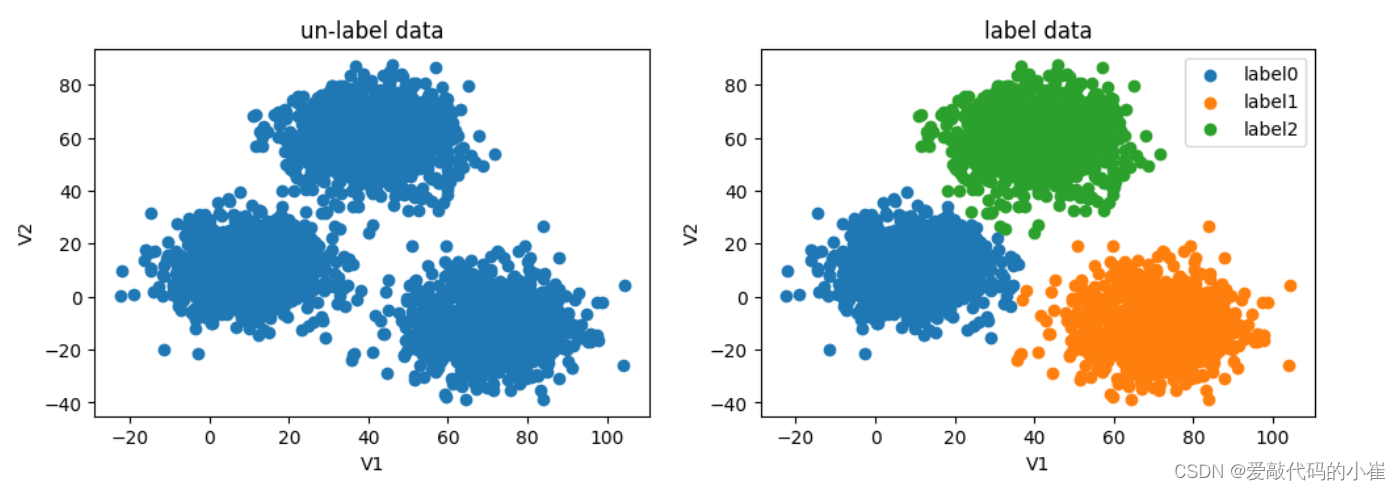
n_clusters是将数据集划分为多少个簇
random_state是确保实验的可重复性以及结果的可复现性
#establish the model and train from sklearn.cluster import KMeans KM = KMeans(n_clusters=3,random_state=0) KM.fit(x)

#求解数据模型中心点 centers = KM.cluster_centers_ print(centers)

fig3 = plt.figure(figsize=(6,4)) plt.scatter(centers[:,0],centers[:,1]) plt.show()
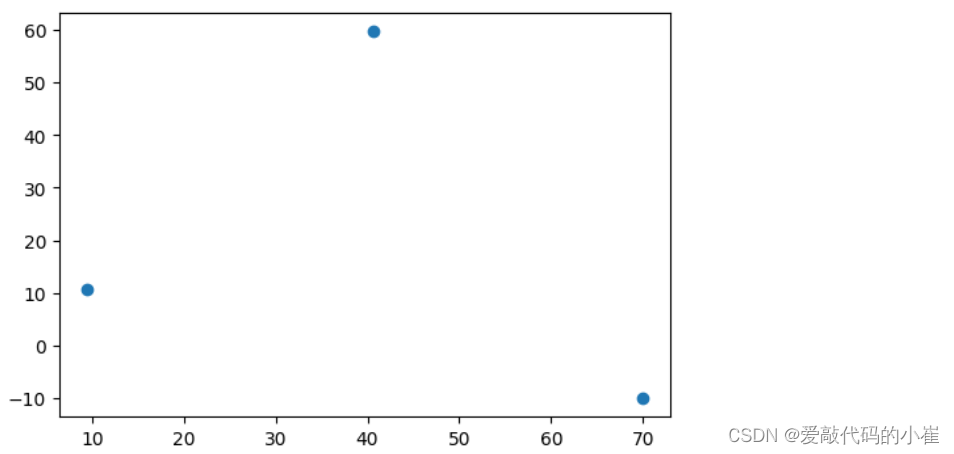
fig4=plt.figure(figsize=(6,4)) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.scatter(centers[:,0],centers[:,1]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()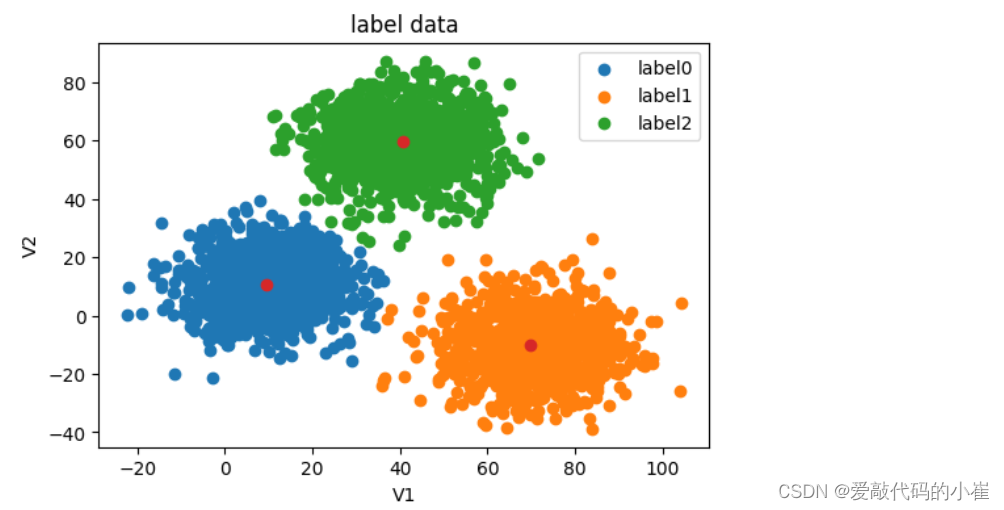
#test data:V1=80,V2=60 y_predict_test=KM.predict([[80,60]]) print(y_predict_test)

value_counts()函数用于统计不同取值出现的频数
#predict based on training data y_predict=KM.predict(x) print(pd.value_counts(y_predict),pd.value_counts(y))

from sklearn.metrics import accuracy_score accuracy=accuracy_score(y,y_predict) print(accuracy)

#visualize the data from matplotlib import pyplot as plt fig=plt.figure(figsize=(12,8)) fig5=plt.subplot(221) label0=plt.scatter(data.loc[:,'V1'][y_predict==0],data.loc[:,'V2'][y_predict==0]) label1=plt.scatter(data.loc[:,'V1'][y_predict==1],data.loc[:,'V2'][y_predict==1]) label2=plt.scatter(data.loc[:,'V1'][y_predict==2],data.loc[:,'V2'][y_predict==2]) plt.scatter(centers[:,0],centers[:,1]) plt.title('predict data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) fig6=plt.subplot(222) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.scatter(centers[:,0],centers[:,1]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()无监督学习预测结果标签与原数据规定标签所对应不上,因为无监督学习没有规定数据标签类别,故需要数据矫正
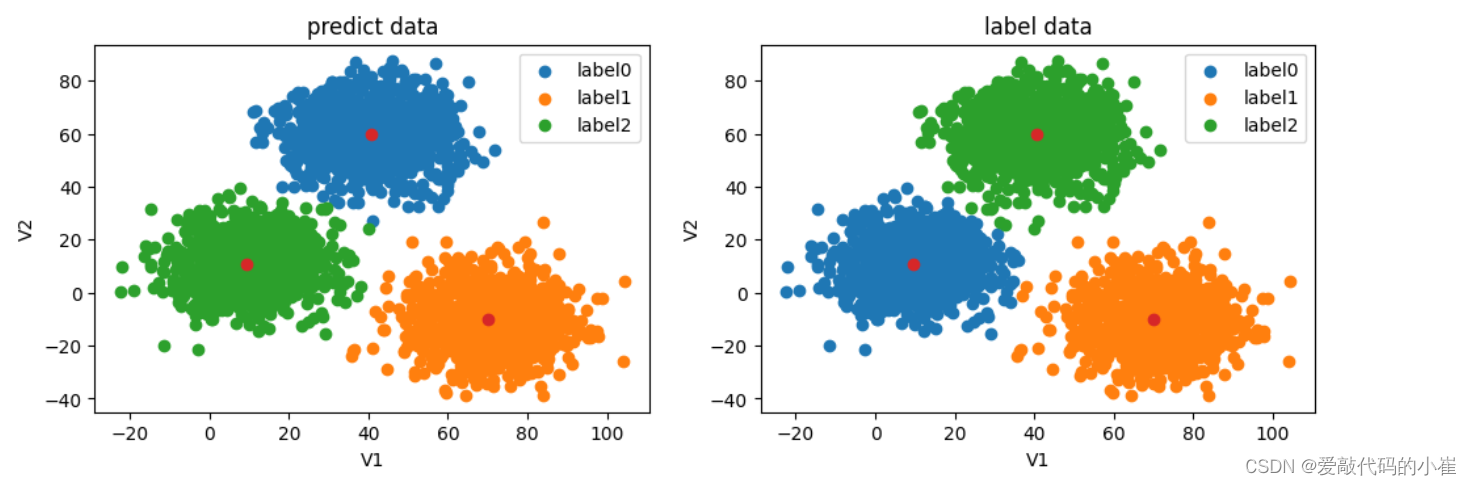
#correct the results 数据矫正 y_corrected=[] for i in y_predict: if i == 0: y_corrected.append(2) elif i == 1: y_corrected.append(1) else: y_corrected.append(0) print(pd.value_counts(y_corrected),pd.value_counts(y))
accuracy_new=accuracy_score(y,y_corrected) print(accuracy_new)
数据矫正后精确度提高

y_corrected=np.array(y_corrected) print(type(y),type(y_corrected))

#visualize the data from matplotlib import pyplot as plt fig=plt.figure(figsize=(12,8)) fig5=plt.subplot(221) label0=plt.scatter(data.loc[:,'V1'][y_corrected==0],data.loc[:,'V2'][y_corrected==0]) label1=plt.scatter(data.loc[:,'V1'][y_corrected==1],data.loc[:,'V2'][y_corrected==1]) label2=plt.scatter(data.loc[:,'V1'][y_corrected==2],data.loc[:,'V2'][y_corrected==2]) plt.scatter(centers[:,0],centers[:,1]) plt.title('corrected data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) fig6=plt.subplot(222) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.scatter(centers[:,0],centers[:,1]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()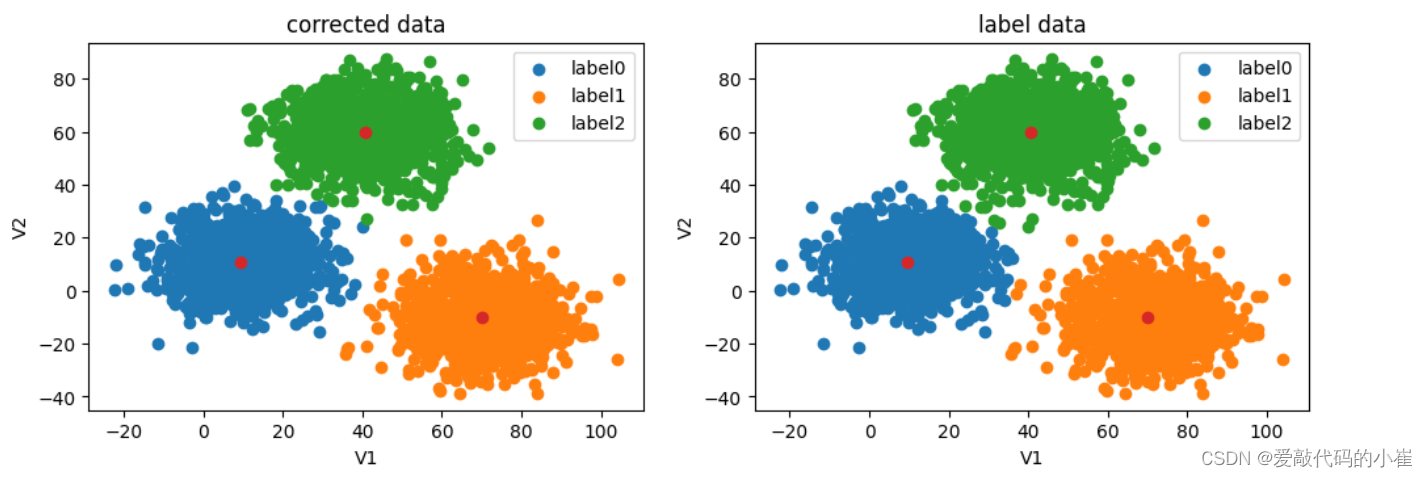
4. 实战(二)
采用KNN算法
#establish a KNN model(KNN监督学习) from sklearn.neighbors import KNeighborsClassifier KN = KNeighborsClassifier() KN.fit(x,y)

#predict based on the test data V1=80,V2=60 y_predict_KNN_test=KN.predict([[80,60]]) y_predict_KNN=KN.predict(x) accuracy_KNN_score=accuracy_score(y,y_predict_KNN) print(y_predict_KNN_test) print(accuracy_KNN_score)

print(pd.value_counts(y),pd.value_counts(y_predict_KNN))

#visualize the data from matplotlib import pyplot as plt fig=plt.figure(figsize=(12,8)) fig5=plt.subplot(221) label0=plt.scatter(data.loc[:,'V1'][y_predict_KNN==0],data.loc[:,'V2'][y_predict_KNN==0]) label1=plt.scatter(data.loc[:,'V1'][y_predict_KNN==1],data.loc[:,'V2'][y_predict_KNN==1]) label2=plt.scatter(data.loc[:,'V1'][y_predict_KNN==2],data.loc[:,'V2'][y_predict_KNN==2]) plt.title('KNN result') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) fig6=plt.subplot(222) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()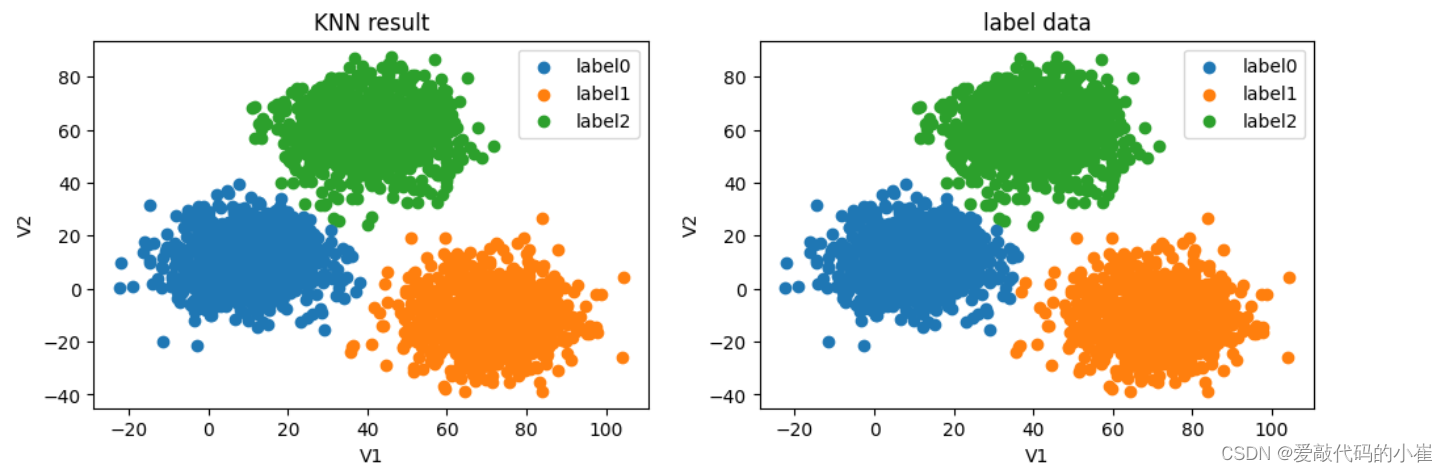
采用Meanshift算法
#try meanshift model from sklearn.cluster import MeanShift,estimate_bandwidth bw=estimate_bandwidth(x,n_samples=3000) print(bw)
计算圆的半径

#train data model MS=MeanShift(bandwidth=bw) MS.fit(x)

y_predict_ms=MS.predict(x) print(pd.value_counts(y),pd.value_counts(y_predict_ms))

#correct the results y_correct_ms=[] for i in y_predict_ms: if i == 0: y_correct_ms.append(2) elif i ==1: y_correct_ms.append(1) else: y_correct_ms.append(0) print(pd.value_counts(y),pd.value_counts(y_correct_ms))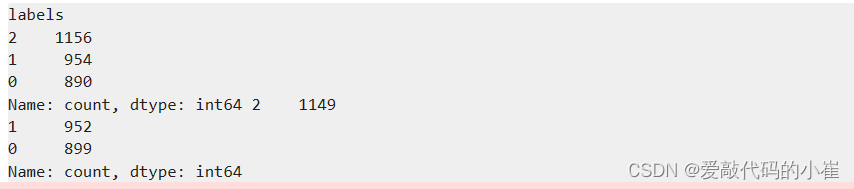
accuracy_ms_score=accuracy_score(y,y_correct_ms) print(accuracy_ms_score)

#covert the results to numpy array y_correct_ms=np.array(y_correct_ms) print(type(y_correct_ms)

#visualize the data from matplotlib import pyplot as plt fig=plt.figure(figsize=(12,8)) fig9=plt.subplot(221) label0=plt.scatter(data.loc[:,'V1'][y_correct_ms==0],data.loc[:,'V2'][y_correct_ms==0]) label1=plt.scatter(data.loc[:,'V1'][y_correct_ms==1],data.loc[:,'V2'][y_correct_ms==1]) label2=plt.scatter(data.loc[:,'V1'][y_correct_ms==2],data.loc[:,'V2'][y_correct_ms==2]) plt.title('ms result') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) fig10=plt.subplot(222) label0=plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0]) label1=plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1]) label2=plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2]) plt.title('label data') plt.xlabel('V1') plt.ylabel('V2') plt.legend((label0,label1,label2),('label0','label1','label2')) plt.show()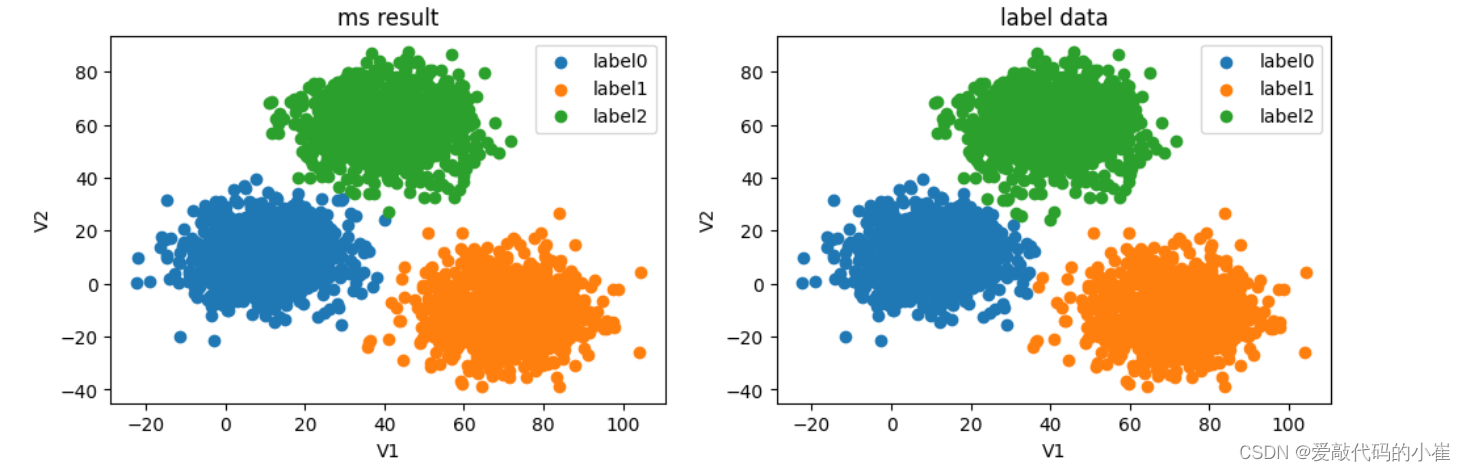
四、机器学习其他常用技术
1.决策树(Dicesion Tree)
-
一种对实例进行分类的树形结构,通过多层判断区分目标所属类别
本质:通过多层判断,从训练数据集中归纳出一组分类规则
-
优点:
- 计算量小,运算速度快
- 易于理解,可清晰查看个属性的重要性
-
缺点:
- 忽略属性间的相关性
- 样本类别分布不均匀时,容易影响模型表现
-
求解方法
ID3:利用信息熵原理选择信息增益最大的属性作为分类属性,递归的拓展决策树的分枝,完成决策树的构造。
信息熵是度量随机变量不确定性的指标,熵越大,变量的不确定性就越大。假定当前样本集合D中第k类样本所占的比例为 p k p_k pk,则D的信息熵为: E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D) = -\sum_{k=1}^{|y|}p_klog_2p_k Ent(D)=−k=1∑∣y∣pklog2pk
根据信息熵,可以计算以属性a进行样本划分带来的信息增益:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V D v D E n t ( D v ) Gain(D,a)=Ent(D) - \sum_{v=1}^V{D^v \over D}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑VDDvEnt(Dv)
V为根据属性a划分出的类别数、D为当前样本总数, D v D^v Dv为类别v样本数
目标:划分后样本分布不确定性尽可能小,即划分后信息熵小,信息增益大
2.异常检测(Anomaly Detection)
基于高斯分布实现异常检测
高斯分布的概率密度函数是:
p ( x ) = 1 δ 2 π e − ( x − μ ) 2 2 σ p(x)={1 \over \delta \sqrt{2\pi}} e^{-{(x-\mu)^2\over 2\sigma}} p(x)=δ2π 1e−2σ(x−μ)2
其中, μ \mu μ为数据均值, σ \sigma σ为标准差:
μ = 1 m ∑ i = 1 m x ( i ) \mu={1 \over m} \sum_{i=1} ^mx(i) μ=m1i=1∑mx(i)
σ 2 = 1 m ∑ i = 1 m ( x ( i ) − μ ) 2 \sigma^2={1 \over m}\sum_{i=1}^m(x(i)-\mu)^2 σ2=m1i=1∑m(x(i)−μ)2
- 计算数据均值 μ \mu μ,标准差 σ \sigma σ
- 计算对应的高斯分布的概率密度函数
- 根据数据点概率,进行判断,如果 p ( x ) p(x) p(x)
数据高于一维时:
{ x 1 ( 1 ) , x 1 ( 2 ) , . . . . . . x 1 ( m ) x n ( 1 ) , x n ( 2 ) , . . . . . . x n ( m ) } \begin{Bmatrix} x_1(1),x_1(2),......x_1(m) \\ x_n(1),x_n(2),......x_n(m) \end{Bmatrix} {x1(1),x1(2),......x1(m)xn(1),xn(2),......xn(m)}
- 计算数据均值
μ
1
,
μ
2
,
.
.
.
.
.
μ
n
\mu_1,\mu_2,.....\mu_n
μ1,μ2,.....μn,标准差
σ
1
,
σ
2
,
.
.
.
.
.
.
σ
n
\sigma_1,\sigma_2,......\sigma_n
σ1,σ2,......σn
μ j = 1 m ∑ i = 1 m x j ( i ) σ j 2 = 1 m ∑ i = 1 m ( x j ( i ) − μ j ) 2 \mu_j={1 \over m}\sum_{i=1}^mx_j(i) \qquad \sigma_j^2={1 \over m} \sum_{i=1}^m(x_j(i)-\mu_j)^2 μj=m1i=1∑mxj(i)σj2=m1i=1∑m(xj(i)−μj)2
- 计算概率密度函数
p
(
x
)
p(x)
p(x)
p ( x ) = ∏ j = 1 n 1 σ j 2 π e − ( x j − μ j ) 2 2 σ 2 p(x) = \prod_{j=1}^n{1 \over \sigma_j \sqrt{2\pi}}e^{-{(x_j-\mu_j)^2 \over 2\sigma^2}} p(x)=j=1∏nσj2π 1e−2σ2(xj−μj)2
3.主成分分析(PCA)
数据降维,是指在某些限定条件下,降低随机变量个数,得到一组“不相关”主变量的过程。
PCA:数据降维方法
目标:寻找k(k
- 概念:
- 从数据中寻找规律、建立关系,根据建立的关系去解决问题的方法。









