PID控制参数整定(调节方法)原理+图示+MATLAB调试
- Chapter1 PID控制参数整定(调节方法)原理+图示+MATLAB调试
- 序
- 一、P参数选取
- 二、I的调节
- 三、D的调节
- 四、总结
- Chapter2 PID参数调整,个人经验(配输出曲线图)
- Chapter3 PID温度控制参数整定方法
- Chapter4 simulink中的PID模块的使用
- 1、Simulink中PID模块的介绍
- 1.1、控制器类型选择
- 1.2、PID控制器格式
- 1.3、时域选择
- 1.4、PID的饱和输出限制
- 2 、自建PID模块
- Chapter5 simulink实现模糊PID控制
- 模糊系统建立
- simulink实现
- 模糊PID模块
- 结果展示
- Chapter6 飞思卡尔智能车----模糊PID算法通俗讲
- 1.1传统PID控制
- 1.2模糊PID控制
- 2.1模糊化
- 2.2 模糊推理
- 2.3 清晰化
- 3 模糊PID
- 4. 部分解释
- Chapter7 模糊自适应整定PID控制
- Chapter8 自适应模糊PID(位置式)C语言实现
- 一、自适应模糊PID原理
- 二、代码实现
- fuzzy_pid.h
- fuzzy_pid.c
- 调用方法
Chapter1 PID控制参数整定(调节方法)原理+图示+MATLAB调试
原文链接:https://blog.csdn.net/viafcccy/article/details/107988093
序
首先最重要的是了解每个参数调节了系统响应的那些属性,通过观察响应从而调节参数改变属性。
PID的作用概述:
1、P产生响应速度和力度,过小响应慢,过大会产生振荡,是I和D的基础。
2、I在有系统误差和外力作用时消除偏差、提高精度,同时也会增加响应速度,产生过冲,过大会产生振荡。
3、D抑制过冲和振荡,过小系统会过冲,过大会减慢响应速度。D的另外一个作用是抵抗外界的突发干扰,阻止系统的突变。
同时调节的顺序是:P>I>D
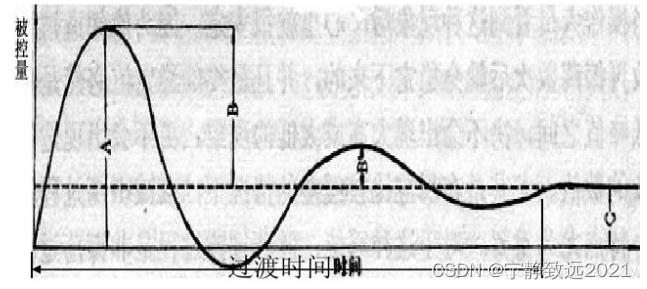
下面了解的一个很重要的就是调节的目标,也就是最好的响应曲线是什么样子。
PID 调节目标:
1、衰减比在4-10之间最佳,也就是响应曲线的前两个峰值B:B1的比值在4-10之间。
2、稳态误差趋近于0
3、系统响应越快越好
一、P参数选取
tip:在第一步牢记P产生响应速度和力度,过小响应慢,过大会产生振荡,是I和D的基础。
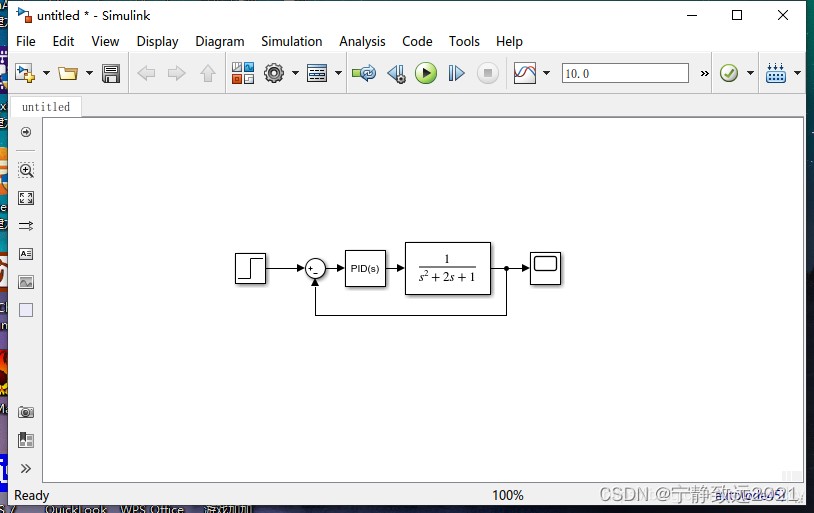
如果想自己调试尝试可以打开matlab,运行simulink,照着下面的图进行连接,如果想直接应用可以直接往后看。
图中的系统为一个PID控制二阶系统。
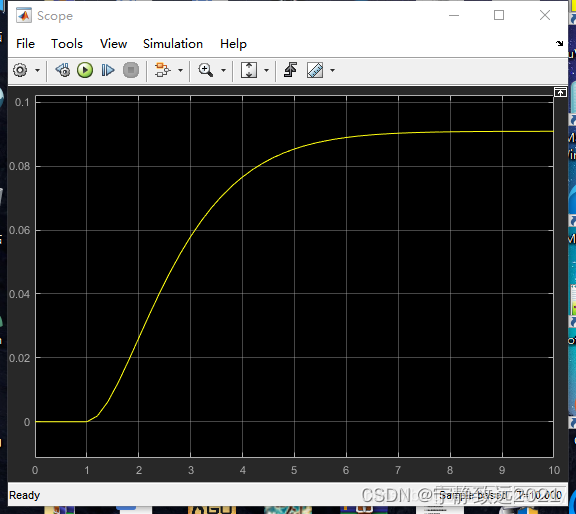
拿上面的系统进行举例,首先设定P=0.1,I=0,D=0观察响应。可以看到图像没有超调,说明P产生的响应速度和力度太小了,
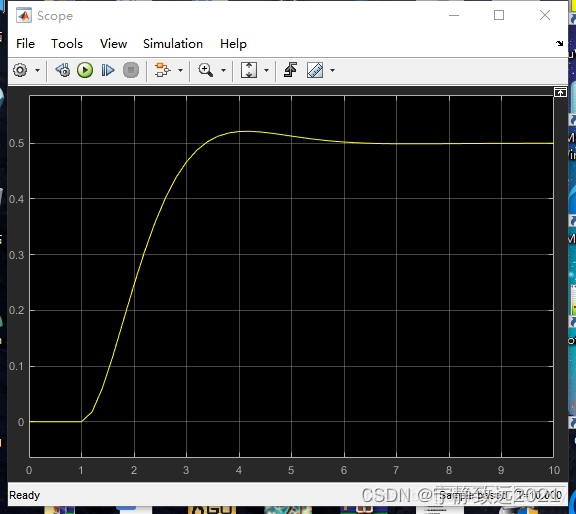
P=1,I=0,D=0观察系统响应,超调量出现但是只有一个波形,同时也就意味着调节时间太慢了,继续加大P
P=10,I=0,D=0,此时调节时间显著下降,可以看到此时的数量级已经调整完成,也就是P参数只需要微调
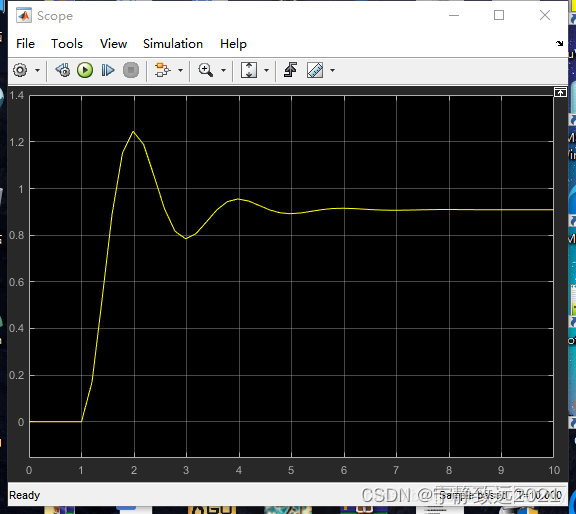
P=100,I=0,D=0,系统开始变得振荡
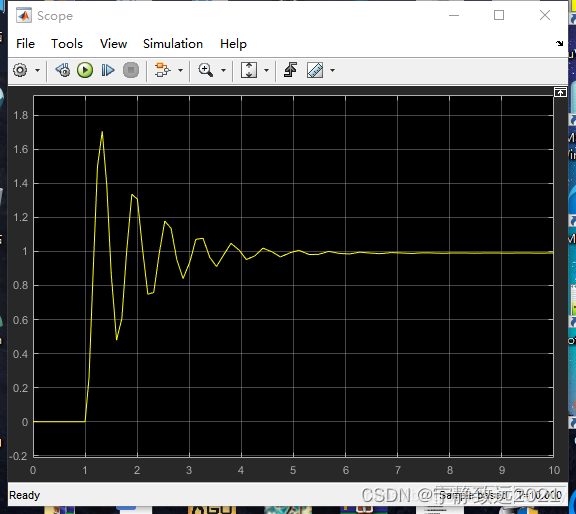
如果继续加大P,系统会达到一个临界值,产生等幅振荡,最后开始发散。如下图所示:
二、I的调节
tip:I在有系统误差和外力作用时消除偏差、提高精度,同时也会增加响应速度,产生过冲,过大会产生振荡。
I主要调节稳态输出,消除扰动。由于系统没有扰动输入因此看不到I对于消除扰动的效果。P=10,I=10,D=0,此时I过大导致系统振荡加剧。
P=10,I=1,D=0,此时响应波形基本符合预期。观察稳态输出约为0.963左右。
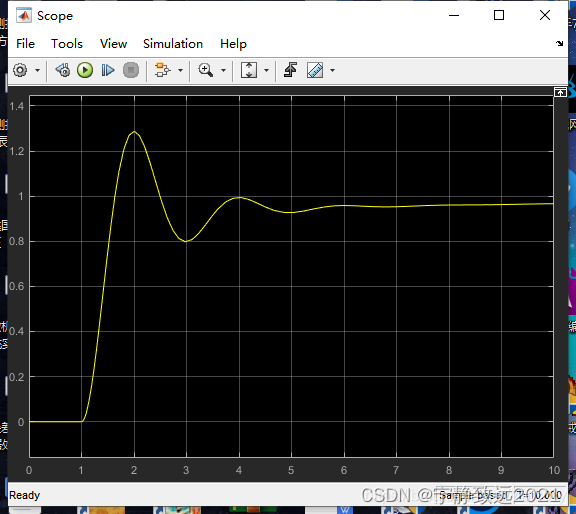
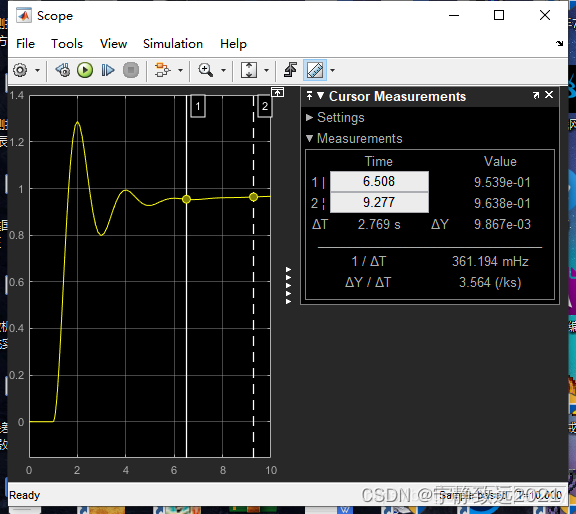
P=10,I=0.1,D=0,可以看到几乎响应波形没有变化。说明在没有扰动的情况下I只要不过大影响不大。但是稳态输出变化为0.916
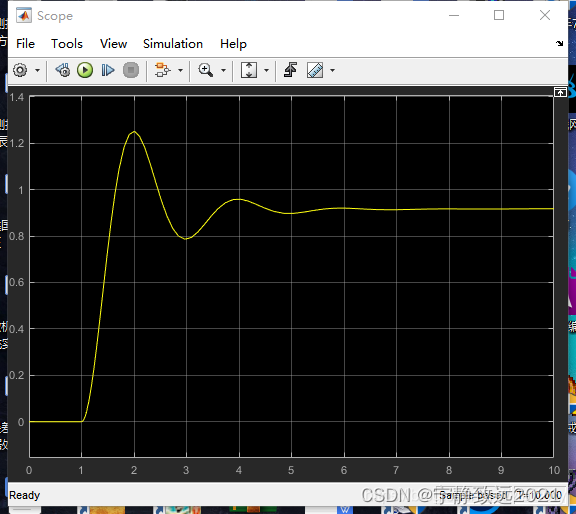
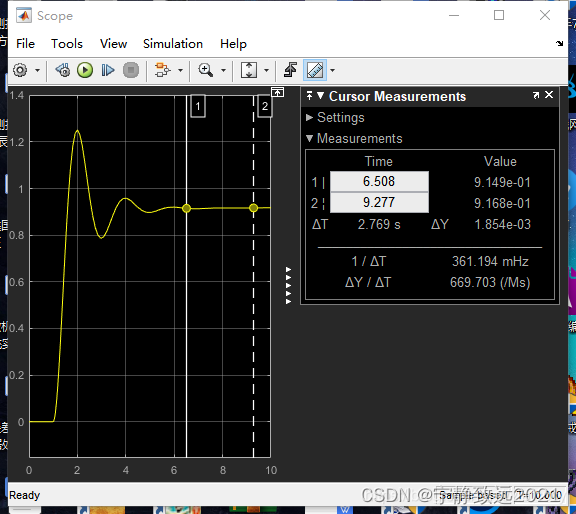
P=10,I=0,D=0,稳态输出变为0.91左右。
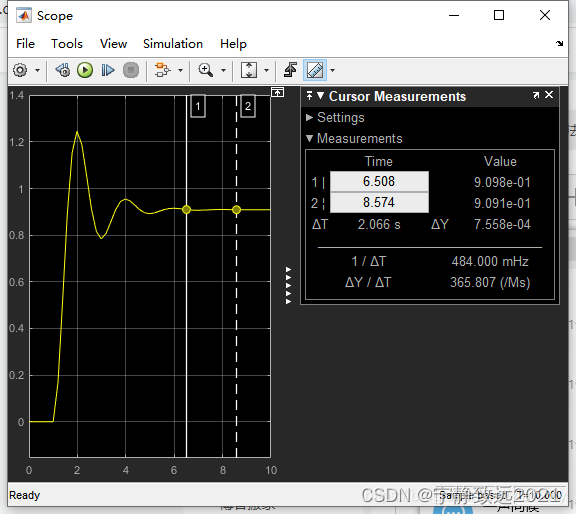
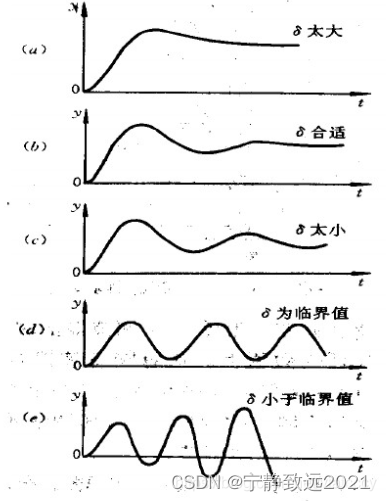
最终我们可以通过I少量调节稳态输出的值,最终将稳态误差消除。关于I对波形影响的作用总结如下图:
三、D的调节
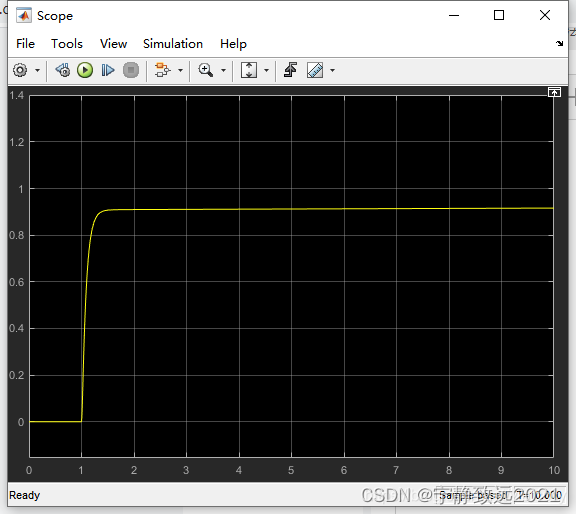
tip:D抑制过冲和振荡,过小系统会过冲,过大会减慢响应速度。D的另外一个作用是抵抗外界的突发干扰,阻止系统的突变。
P=10,I=0.1,D=10,可以看到将所有的冲击都消除掉了。
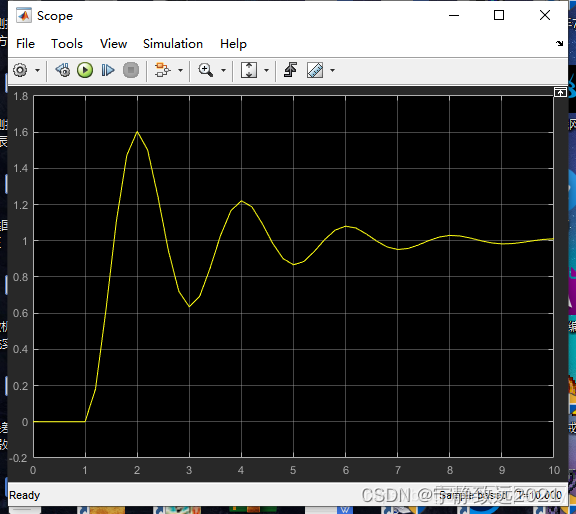
P=10,I=0.1,D=1,消除冲击减弱,此时显然衰减比不符合要求
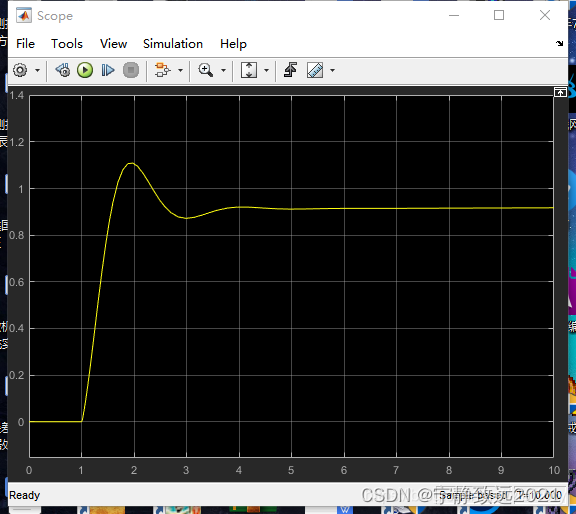
P=10,I=0.1,D=1,此时基本符合要求。
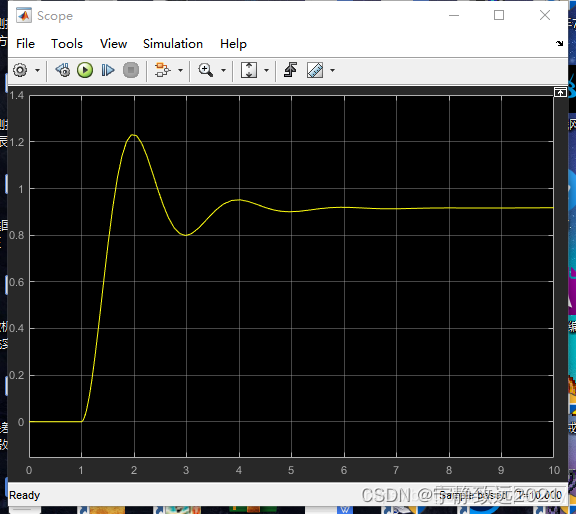
四、总结
首先调节P的数量级达到一个只有2个左右明显峰值的波形,再调节I找到不会波形振荡也不会没有超调的的区间,在区间内找到一个I将稳态误差尽可能消除。最终使用D来控制衰减比和波形的峰值、超调量。最后根据要求的稳态值、调节时间、超调量、上升时间、峰值时间等指标进行微调达到目标。
最后可以总结成一个口诀
参数整定找最佳,从小到大顺序查,
先是比例后积分,最后再把微分加,
曲线振荡很频繁,比例度盘要放大,
曲线漂浮绕大湾,比例度盘往小扳,
曲线偏离回复慢,积分时间往下降,
曲线波动周期长,积分时间再加长,
曲线振荡频率快,先把微分降下来,
动差大来波动慢,微分时间应加长,
理想曲线两个波,前高后低4比1,
一看二调多分析,调节质量不会低 。
Chapter2 PID参数调整,个人经验(配输出曲线图)
原文链接:https://blog.csdn.net/weixin_44407238/article/details/119255699
Chapter3 PID温度控制参数整定方法
原文链接:https://blog.csdn.net/pengzhihui2012/article/details/50380780
最近做了一个温度控制相关的项目,在此记录一下,方便以后查找,同时也供大家参考,欢迎指正,所有数据均为实验数据,绝对真实。
-
位置式PID控制公式原型:u(t) = kp * e(t) + ki * [e(1) + e(2) + ....+ e(t)] + kd * [e(t) - e(t-1)]
-
控制对象:加热/制冷器(在2分钟内不能再加热至冷之间切换)控制密封的腔体(空间体积大小15cm*20cm*65cm)温度。
-
控制原理:利用MCU的输出比较模块(OCM)产生PWM波驱动H桥电路(通过目标温度和环境温度对比决定加热或者制冷)。
-
PID参数整定
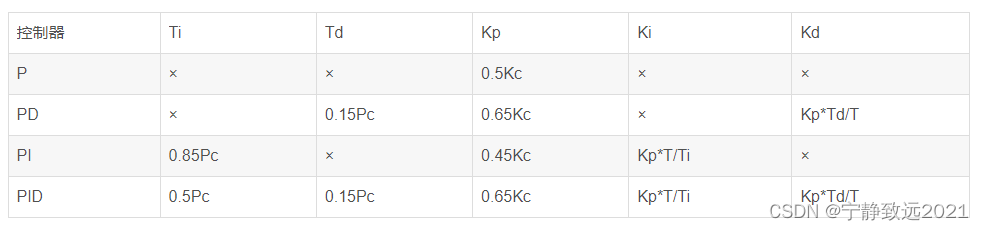
参数说明:
Kc: 只采用比例环节控制条件下,控制系统的稳态误差尽量达到最小时的Kp值。
Pc: 只采用比例环节控制条件下,控制系统的震荡周期。
Ti: 控制系统的积分时间。
Td: 控制系统的微分时间。
T: PID控制采样计算周期。
Kp、Ki、Kd:被整定的参数。
1):获取合适的Kc值,设置Ki,Kd为0。在当前温度进入目标温度3.5°内开始进行PID控制,之前采用90%恒定功率加热。
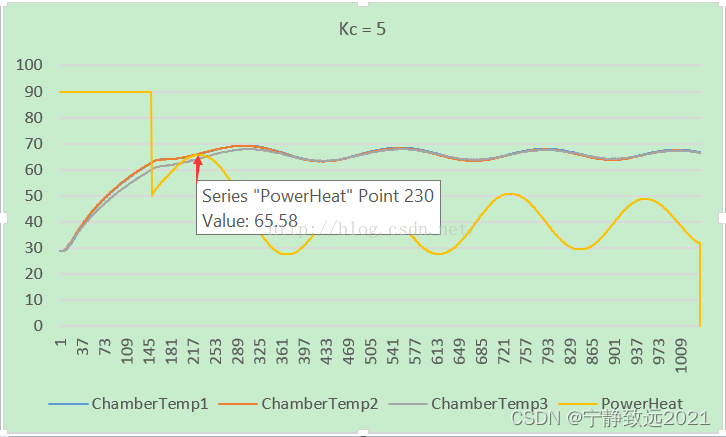
图一(Kc =5)
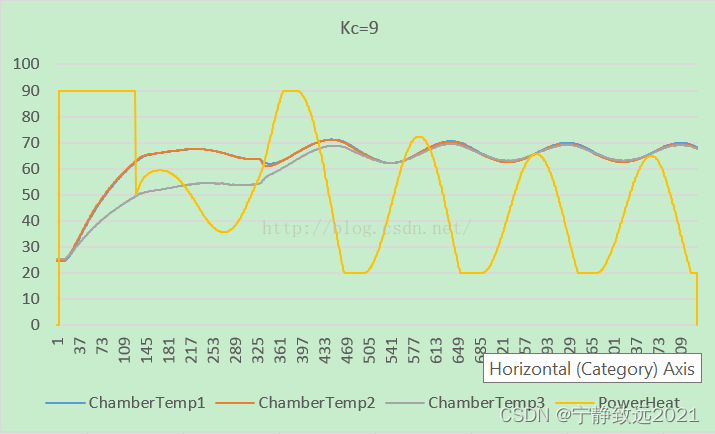
图二(Kc =9)
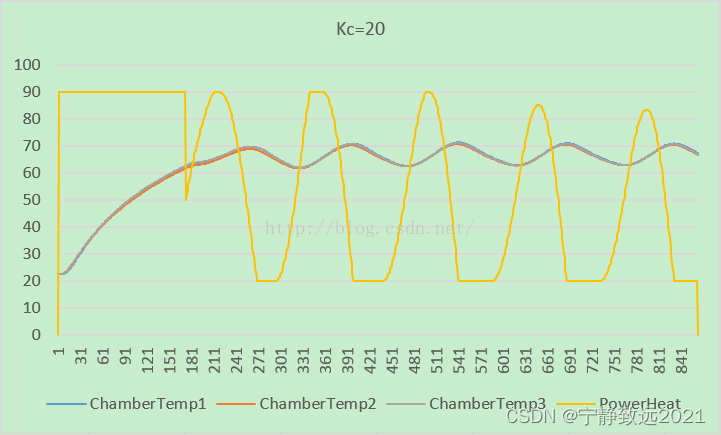
图三(Kc =20)
从上述的四组数据中可以看到,当Kc=5时,控制系统的稳态误差是最小的。在目标范围正负3°之间,选取Kc = 5.
2):计算Pc值。从上述的图一(将.csv格式的数据文件在excel中转换图表,将鼠标放在曲线上,会自动显示此点的坐标,如图所示),取4个震荡周期一共720个点,得出一个震荡周期为Pc=720*5/4= 900s。
3):根据个人需要采用哪种PID组合来计算Ti、Td、Kp、Ki、Kd。温度控制是属于滞后控制,而PID控制中的,微分项是具有超前调节的作用,因此必须引入;积分项对误差的作用取决于时间的积分,随着时间的增加,积分项会增大。这样,即便误差很小,积分项也会随着时间的增加而加大,推动控制器的输出向稳态误差减小的方向变化,直到稳态误差等于零。我采用的是PID组合来控制。得出Ti=9000.5=450s。Td=9000.15=135s。
Kp=50.65=3.25;Ki= KpT/Ti=3.255/450=0.036;Kd= KpTd/T=3.25*135s /5=88。
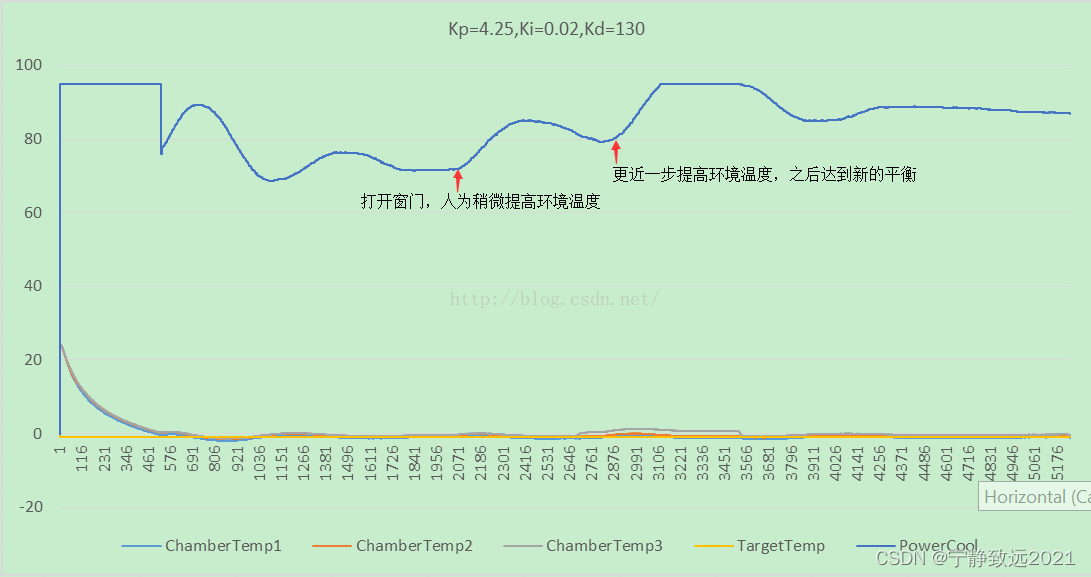
4):采用PID控制温度,无论高温低温,稳态误差均在正负0.5°范围之内。如下所示:
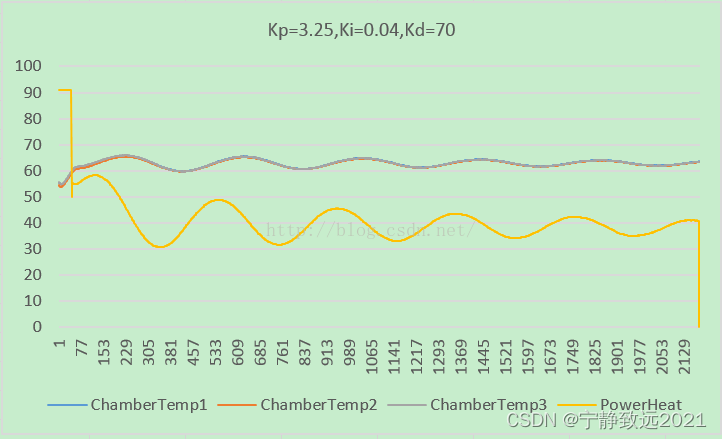
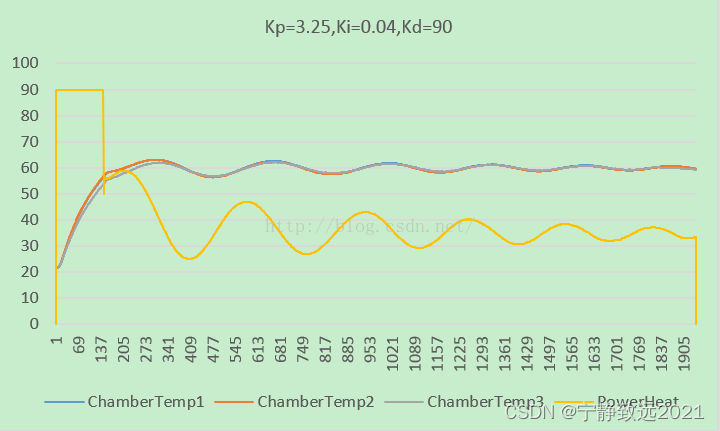
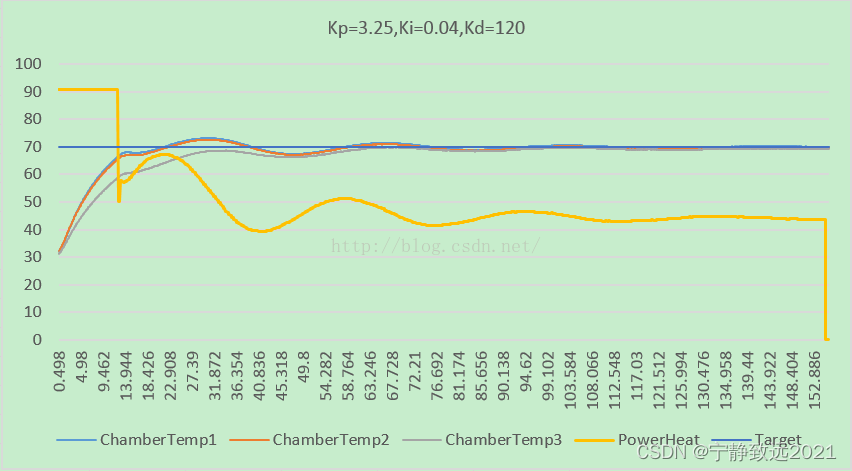
一般根据模型计算的参数不一定是适合所有的控制系统(这里实验得到的最佳Kd值为120,而我们算出来的是88),根据特定的环境调节参数范围,找到最优参数,因本系统是滞后系统,微分项起主导作用,我暂时还只做了调整kd值的实验,Ki一般反应在系统达到稳态的时候是否存在稳定误差,从实验结果得出,稳态误差几乎可以忽略。
零下一度的目标温度,连续8小时的温度控制数据:
附录://PWM频率为1Khz,定时器的计数周期为5000(mPID.MaxDuty = 5000*90%),PID返回值和上次的的定时器技术值决定本次的占空比。
INT32 PID_calculate(double CurTemp) { INT32 RetValue; doubleresult_value; // Keep previouserror mPID.PrevError =mPID.Error; // calculatecurrent error mPID.Error =mPID.Target - CurTemp; // calculateintegral mPID.SumError +=mPID.Error; if(mPID.Kd >0.0001) { result_value =mPID.Kp * mPID.Error + mPID.SumError * mPID.Ki + mPID.Kd* (mPID.Error - mPID.PrevError); } else { result_value =mPID.Kp * mPID.Error + mPID.SumError * mPID.Ki; } RetValue =(INT32)result_value; return RetValue; } //Timer interrupt enable control flag, execute temperaturecontrol. // void TemperatureControl() { INT32 ret = 0; if(mPID.type ==HEAT) { INT32 DutyValue= OC4RS; if(fabs(mPID.Current- mPID.Target) PIDControlStartPoint = 12; ret =PID_calculate(mPID.Current); } elseif(fabs(mPID.Current - mPID.Target) OC4RS = INITPWMPERIOD16 * 50 / 100.0; ret = 0; return ; } else { ret = 0; } if( (DutyValue+ ret) mPID.MaxDuty) OC4RS =mPID.MaxDuty; else if(DutyValue+ ret output_num = output_num; fuzzy_struct->mf_type = (unsigned int *) malloc((input_num + output_num) * sizeof(unsigned int)); #ifdef fuzzy_pid_rule_base_deep_copy fuzzy_struct->mf_params = (int *) malloc(4 * qf_default * sizeof(int)); fuzzy_struct->rule_base = (int *) malloc(output_num * qf_default * qf_default * sizeof(int)); #endif fuzzy_struct->output = (float *) malloc(output_num * sizeof(float)); return fuzzy_struct; } void delete_fuzzy(struct fuzzy *fuzzy_struct) { free(fuzzy_struct->mf_type); free(fuzzy_struct->output); free(fuzzy_struct); } void fuzzy_params_init(struct fuzzy *fuzzy_struct, unsigned int mf_type, unsigned int fo_type, unsigned int df_type, int mf_params[], int rule_base[][qf_default]) { for (unsigned int i = 0; i input_num + fuzzy_struct->output_num; ++i) { fuzzy_struct->mf_type[i] = mf_type; } for (unsigned int i = 0; i output_num; ++i) { fuzzy_struct->output[i] = 0; } #ifdef fuzzy_pid_rule_base_deep_copy for (unsigned int j = 0; j mf_params[j] = mf_params[j]; } for (unsigned int k = 0; k output_num * qf_default; ++k) { for (unsigned int i = 0; i rule_base[k * 7 + i] = rule_base[k][i]; } } #else fuzzy_struct->mf_params = mf_params; fuzzy_struct->rule_base = (int *) rule_base; #endif fuzzy_struct->fo_type = fo_type; fuzzy_struct->df_type = df_type; } #define inverse(parameter) 1.0f/(float)parameter // Gaussian membership function float gaussmf(float x, float sigma, float c) { return expf(-powf(((x - c) / sigma), 2.0f)); } // Generalized bell-shaped membership function float gbellmf(float x, float a, float b, float c) { return inverse(1.0f + powf(fabsf((x - c) / a), 2.0f * b)); } // Sigmoidal membership function float sigmf(float x, float a, float c) { return inverse(1.0f + expf(a * (c - x))); } // Trapezoidal membership function float trapmf(float x, float a, float b, float c, float d) { if (x >= a && x = b && x = c && x return trapmf(x, a, b, b, c); } // Z-shaped membership function float zmf(float x, float a, float b) { if (x switch (mf_type) { case 0: return gaussmf(x, params[0], params[1]); case 1: return gbellmf(x, params[0], params[1], params[2]); case 2: return sigmf(x, params[0], params[2]); case 3: return trapmf(x, params[0], params[1], params[2], params[3]); case 5: return zmf(x, params[0], params[1]); default: // set triangular as default membership function return trimf(x, params[0], params[1], params[2]); } } // Union operator float or (float a, float b, unsigned int type) { if (type == 1) // algebraic sum { return a + b - a * b; } else if (type == 2) // bounded sum { return fminf(1, a + b); } else // fuzzy union { return fmaxf(a, b); } } // Intersection operator float and (float a, float b, unsigned int type) { if (type == 1) // algebraic product { return a * b; } else if (type == 2) // bounded product { return fmaxf(0, a + b - 1); } else // fuzzy intersection { return fminf(a, b); } } // Equilibrium operator float equilibrium(float a, float b, float params) { return powf(a * b, 1 - params) * powf(1 - (1 - a) * (1 - b), params); } // Fuzzy operator float fo(float a, float b, unsigned int type) { if (type output_num*sizeof(float)); for (unsigned int l = 0; l output_num; ++l) { numerator_count[l] = 0; } for (int i = 0; i output_num; ++k) { for (unsigned int i = 0; i rule_base[k * qf_default * qf_default + index[i] * qf_default + index[count[0] + j]]; } } } #ifdef fuzzy_pid_debug_print printf("output:\n"); #endif for (unsigned int l = 0; l output_num; ++l) { fuzzy_struct->output[l] = numerator_count[l] / denominator_count; #ifdef fuzzy_pid_debug_print printf("%f,%f,%f\n", numerator_count[l], denominator_count, fuzzy_struct->index[l]); #endif } free(numerator_count);//有借有还再借不难 } // Defuzzifier void df(const float *joint_membership, const unsigned int *output, const unsigned int *count, struct fuzzy *fuzzy_struct, int df_type) { if (df_type == 0) moc(joint_membership, output, count, fuzzy_struct); else { printf("Waring: No such of defuzzifier!\n"); moc(joint_membership, output, count, fuzzy_struct); } } void fuzzy_control(float e, float de, struct fuzzy *fuzzy_struct) { float membership[qf_default * 2]; // Store membership unsigned int index[qf_default * 2]; // Store the index of each membership unsigned int count[2] = {0, 0}; { int j = 0; for (int i = 0; i mf_type[0], fuzzy_struct->mf_params + 4 * i); // if (temp > 1e-4) // { membership[j] = temp; index[j++] = i; // } } count[0] = j; for (int i = 0; i mf_type[1], fuzzy_struct->mf_params + 4 * i); // if (temp > 1e-4) // { membership[j] = temp; index[j++] = i; // } } count[1] = j - count[0]; } #ifdef fuzzy_pid_debug_print printf("membership:\n"); for (unsigned int k = 0; k output_num; ++l) { fuzzy_struct->output[l] = 0; } return; } // Joint membership //注意 TI的C99编译器并不是完全支持动态数组的特性,所以这里改变了一下(c89写法) // float joint_membership[count[0] * count[1]]; float *joint_membership= (float *)malloc(count[0] * count[1]*sizeof(float)); for (int i = 0; i fo_type); } } df(joint_membership, index, count, fuzzy_struct, 0); free(joint_membership); } struct PID *raw_fuzzy_pid_init(float kp, float ki, float kd, float integral_limit, float dead_zone, float feed_forward, float error_max, float delta_error_max, float delta_kp_max, float delta_ki_max, float delta_kd_max, unsigned int mf_type, unsigned int fo_type, unsigned int df_type, int mf_params[], int rule_base[][qf_default], int output_min_value, int output_middle_value, int output_max_value) { struct PID *pid = (struct PID *) malloc(sizeof(struct PID)); pid->kp = kp; pid->ki = ki; pid->kd = kd; pid->delta_kp_max = delta_kp_max; pid->delta_ki_max = delta_ki_max; pid->delta_kd_max = delta_kd_max; pid->delta_kp = 0; pid->delta_ki = 0; pid->delta_kd = 0; pid->error_max = error_max; pid->delta_error_max = delta_error_max; int output_count = 1; if (ki > 1e-4) { output_count += 1; if (kd > 1e-4) output_count += 1; } pid->fuzzy_struct = fuzzy_init(2, output_count); fuzzy_params_init(pid->fuzzy_struct, mf_type, fo_type, df_type, mf_params, rule_base); pid->last_error = 0; pid->current_error = 0; pid->intergral = 0; pid->intergral_limit = integral_limit; pid->dead_zone = dead_zone; pid->feed_forward = feed_forward; pid->output_max_value = output_max_value; pid->output_middle_value = output_middle_value; pid->output_min_value = output_min_value; return pid; } struct PID *fuzzy_pid_init(float *params, float delta_k, unsigned int mf_type, unsigned int fo_type, unsigned int df_type, int mf_params[], int rule_base[][qf_default]) { return raw_fuzzy_pid_init(params[0], params[1], params[2], params[3], params[4], params[5], max_error, max_delta_error, params[0] / delta_k, params[1] / delta_k, params[2] / delta_k, mf_type, fo_type, df_type, mf_params, rule_base, min_pwm_output, middle_pwm_output, max_pwm_output); } int round_user(float parameter) { if ((int)(parameter * 10.0) % 10 >= 5) return parameter + 1; else return parameter; } int limit(int value, int max_limit, int min_limit) { if (value > max_limit) return max_limit; if (value max_limit) return max_limit; if (value last_error = pid->current_error; pid->current_error = idea - real; float delta_error = pid->current_error - pid->last_error; float uk; #ifdef fuzzy_pid_dead_zone if (pid->current_error dead_zone && pid->current_error > -pid->dead_zone) { pid->current_error = 0; } else { if (pid->current_error > pid->dead_zone) pid->current_error = pid->current_error - pid->dead_zone; else { if (pid->current_error dead_zone) pid->current_error = pid->current_error + pid->dead_zone; } } #endif //关键代码 fuzzy_control(pid->current_error / pid->error_max * 3.0f, delta_error / pid->delta_error_max * 3.0f, pid->fuzzy_struct); // pid->delta_kp = limits(pid->fuzzy_struct->output[0]/3.0f * pid->delta_kp_max, pid->delta_kp_max ,-pid->delta_kp_max); pid->delta_kp = limits(pid->fuzzy_struct->output[0], pid->delta_kp_max ,-pid->delta_kp_max); if (pid->fuzzy_struct->output_num >= 2) // pid->delta_ki = limits(pid->fuzzy_struct->output[1]/3.0f * pid->delta_ki_max, pid->delta_ki_max ,-pid->delta_ki_max); pid->delta_ki = limits(pid->fuzzy_struct->output[1], pid->delta_ki_max ,-pid->delta_ki_max); else pid->delta_ki = 0; if (pid->fuzzy_struct->output_num >= 3) // pid->delta_kd =limits(pid->fuzzy_struct->output[2]/3.0f * pid->delta_kd_max, pid->delta_kd_max ,-pid->delta_kd_max); pid->delta_kd =limits(pid->fuzzy_struct->output[2], pid->delta_kd_max ,-pid->delta_kd_max); else pid->delta_kd = 0; #ifdef fuzzy_pid_debug_print printf("kp : %f, ki : %f, kd : %f\n", pid->kp + pid->delta_kp, pid->ki + pid->delta_ki, pid->kd + pid->delta_kd); #endif // printf("kpkikd:%f,%f,%f,%f\n", pid->kp + pid->delta_kp, pid->ki + pid->delta_ki, pid->kd + pid->delta_kd,0.0); pid->intergral += (pid->ki + pid->delta_ki) * pid->current_error; #ifdef fuzzy_pid_integral_limit if (pid->intergral > pid->intergral_limit) pid->intergral = pid->intergral_limit; else { if (pid->intergral intergral_limit) pid->intergral = -pid->intergral_limit; } #endif // //这里位置式PID算法 // pid->output = (pid->kp + pid->delta_kp) * pid->current_error + pid->intergral + // (pid->kd + pid->delta_kd) * (pid->current_error - pid->last_error); uk = (pid->kp + pid->delta_kp) * pid->current_error + pid->intergral + (pid->kd + pid->delta_kd) * (pid->current_error - pid->last_error); // pid->output += pid->feed_forward * (float) idea; uk +=pid->feed_forward * (float) idea;//前馈环节 pid->output = uk; //限幅 if(pid->outputoutput_min_value) pid->output=pid ->output_min_value; else if (pid->output>pid ->output_max_value) pid->output=pid ->output_max_value; return pid->output; } void delete_pid(struct PID *pid) { if (pid->fuzzy_struct != NULL) { delete_fuzzy(pid->fuzzy_struct); } free(pid); } void delete_pid_vector(struct PID **pid_vector, unsigned int count) { for (unsigned int i = 0; i output_middle_value, fuzzy_pid_control(real, idea, pid), direct), pid->output_max_value, pid->output_min_value); }调用方法
//全局变量定义方式 struct PID **pid_vector; //main函数中初始化 int rule_base[][qf_default] = { //delta kp rule base {PB, PB, PM, PM, PS, ZO, ZO}, {PB, PB, PM, PS, PS, ZO, NS}, {PM, PM, PM, PS, ZO, NS, NS}, {PM, PM, PS, ZO, NS, NM, NM}, {PS, PS, ZO, NS, NS, NM, NM}, {PS, ZO, NS, NM, NM, NM, NB}, {ZO, ZO, NM, NM, NM, NB, NB}, //delta ki rule base {NB, NB, NM, NM, NS, ZO, ZO}, {NB, NB, NM, NS, NS, ZO, ZO}, {NB, NM, NS, NS, ZO, PS, PS}, {NM, NM, NS, ZO, PS, PM, PM}, {NM, NS, ZO, PS, PS, PM, PB}, {ZO, ZO, PS, PS, PM, PB, PB}, {ZO, ZO, PS, PM, PM, PB, PB}, //delta kd rule base {PS, NS, NB, NB, NB, NM, PS}, {PS, NS, NB, NM, NM, NS, ZO}, {ZO, NS, NM, NM, NS, NS, ZO}, {ZO, NS, NS, NS, NS, NS, ZO}, {ZO, ZO, ZO, ZO, ZO, ZO, ZO}, {PB, PS, PS, PS, PS, PS, PB}, {PB, PM, PM, PM, PS, PS, PB}}; // Default parameters of membership function int mf_params[4 * qf_default] = {-3, -3, -2, 0, -3, -2, -1, 0, -2, -1, 0, 0, -1, 0, 1, 0, 0, 1, 2, 0, 1, 2, 3, 0, 2, 3, 3, 0}; float fuzzy_pid_params[1][pid_params_count] = {{25.4597502f, 10.0053997f, 15.59500027f, 1800, 0, 0, 1}}; struct PID **subpid_vector = fuzzy_pid_vector_init(fuzzy_pid_params, 4.0f, 4, 1, 0, mf_params, rule_base, 1); pid_vector=subpid_vector; //中断中调用 control_uk = fuzzy_pid_control(Voltage_Real, pid.Ref, pid_vector[0]); if(control_uk2800) control_uk=2800; -









