【C++练级之路】【Lv.20】位图和布隆过滤器（揭开大数据背后的神秘面纱）

文章目录

• 引言
• 一、位图
• • 1.1 位图的概念
  • 1.2 位图的优势
  • 1.3 位图的模拟实现
  • • 1.3.1 成员变量与默认成员函数
    • 1.3.2 test
    • 1.3.3 set
    • 1.3.4 reset
    • 1.4 位图的缺陷
    • 1.5 位图的应用场景
    • 二、布隆过滤器
    • • 2.1 布隆过滤器的概念
      • 2.2 布隆过滤器的优势
      • 2.3 布隆过滤器的模拟实现
      • • 2.3.1 成员变量
        • 2.3.2 test
        • 2.3.3 set
        • 2.3.4 哈希化
        • 2.4 布隆过滤器的缺陷
        • 2.5 布隆过滤器的应用场景
        • 三、哈希表、位图和布隆过滤器的对比
        • • 3.1 表格对比
          • 3.2 分析对比

            引言

            哈希映射的思想，在实际中有许多运用，之前介绍的哈希表是一种经典的应用场景，而今天我们将了解其他的哈希数据结构——位图和布隆过滤器，它们在面对海量数据的场景时，有着得天独厚的优势。

            一、位图

            1.1 位图的概念

            位图（bitset），主要用于存储和管理数据的状态。它通过使用位（bit）来表示数据的存在与否，每个位只能存储0或1，分别代表数据不存在和存在。

            

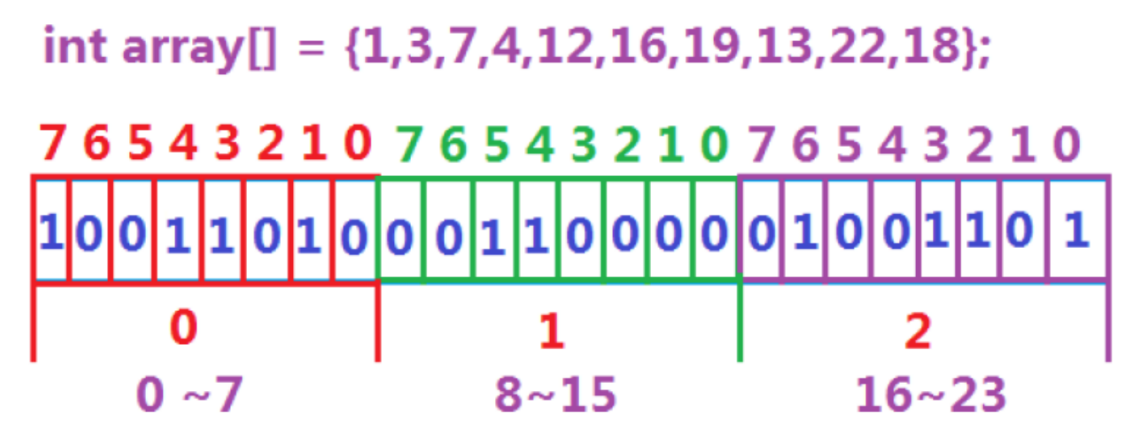
            位图原理：哈希直接定址法

            1.2 位图的优势

            先来看一道面试题：

            给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

            分析：

            1. 首先分析数据量大小，40亿整数 == 160亿byte，而1G约为10亿byte，所以大小约为16G
            2. 快速查找，我们想到哈希表，但是数据量太大，动态内存（最大约为4G）放不下

            ---

            这时，就体现出位图的用处了！

            如果将每个整数以比特位的形式存储表示，那么只需要40亿bit，约为0.5G。

            所以，位图的主要优势为：

            • 查找速度快
            • 节省存储空间

              1.3 位图的模拟实现

              1.3.1 成员变量与默认成员函数

              template
              class bitset
              {
              public:
              	bitset()
              	{
              		_bits.resize(N / 8 + 1);
              	}
              protected:
              	vector _bits;
              	size_t _n = 0;//有效数据个数
              };
              

              细节：

              1. 非类型模板参数N，表示数据量（方便开辟足够空间）
              2. vector数据类型为char，方便进行位操作
              3. 构造函数提前开辟足够的空间（+1防止整除误差）

              1.3.2 test

              检测指定值是否存在

              bool test(size_t x)
              {
              	size_t i = x / 8, j = x % 8;
              	return _bits[i] & (1 
              	size_t i = x / 8, j = x % 8;
              	if (!test(x))
              	{
              		_bits[i] |= (1 
              	size_t i = x / 8, j = x % 8;
              	if (test(x))
              	{
              		_bits[i] &= ~(1 
              public:
              protected:
              	bitset
              	size_t len = N * X;
              	size_t i1 = Hash1()(key) % len;
              	size_t i2 = Hash2()(key) % len;
              	size_t i3 = Hash3()(key) % len;
              	return _bs.test(i1) && _bs.test(i2) && _bs.test(i3);
              }
              
              	size_t len = N * X;
              	size_t i1 = Hash1()(key) % len;
              	size_t i2 = Hash2()(key) % len;
              	size_t i3 = Hash3()(key) % len;
              	_bs.set(i1);
              	_bs.set(i2);
              	_bs.set(i3);
              }
              
              	size_t operator()(const string& s)
              	{
              		size_t hash = 0;
              		for (auto& ch : s)
              		{
              			hash = hash * 31 + ch;
              		}
              		return hash;
              	}
              };
              struct APHash
              {
              	size_t operator()(const string& s)
              	{
              		size_t hash = 0;
              		for (long i = 0; i