模式串匹配——KMP算法
KMP算法一直是一个比较难以理解的算法,本篇文章主要根据《大话数据结构》中关于KMP算法的讲解,结合自己的思考,对于KMP算法进行一个比较详细的解释。
由于博主本人水平有限,难免会出现一些错误。如果发现文章中存在错误敬请批评指正,感谢您的阅读。
字符串模式匹配介绍
相信学习过数据结构与算法的同学一定不会对字符串感到陌生,字符串的逻辑结构与线性表很类似,不同之处是字符串中的元素都是字符。对于字符串这一数据结构,寻找字符串中子串的位置是最重要的操作之一,查找字串位置的操作通常称为串的模式匹配。而KMP算法就是一种字符串模式匹配算法,在介绍KMP算法之前,我们首先了解以下朴素的模式匹配算法是怎样进行的。
朴素的模式匹配算法
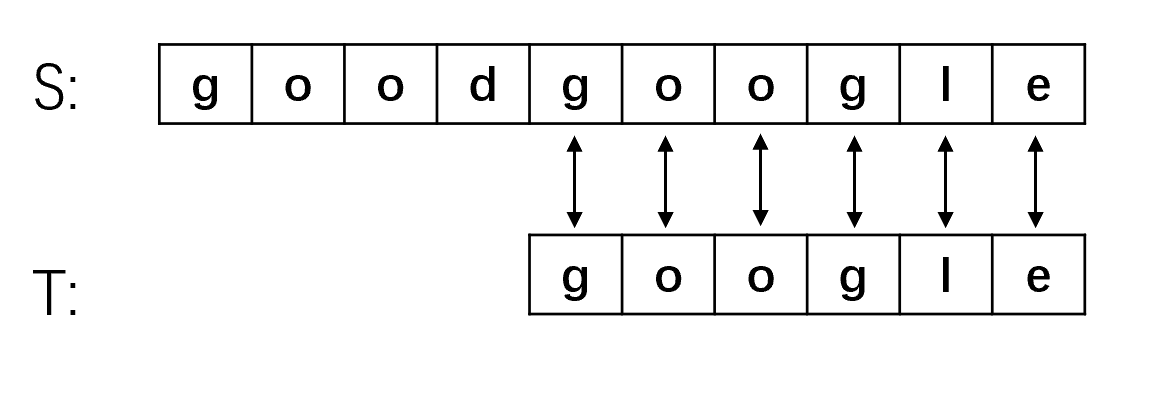
假设我们的主串S=“goodgoogle”,子串T=“google”,我们需要在主串中找到子串的位置,比较朴素的想法是用两个指针(指针其实也就是下标i,j)分别指向主串和子串,如果两个指针指向的元素相同则指针后移,不相同则需要回退指针(主串指针回退到上次匹配首位的下一个位置,子串指针回退到开头位置),重复进行上述操作直到主串指针指向主串末尾,即如下所示:
(1) 从主串S的第一位开始,S与T的前三位都匹配成功,第四位匹配失败,此时将主串的指针退回到第二位,子串的指针退回子串开始,即从S[1]开始重新匹配。
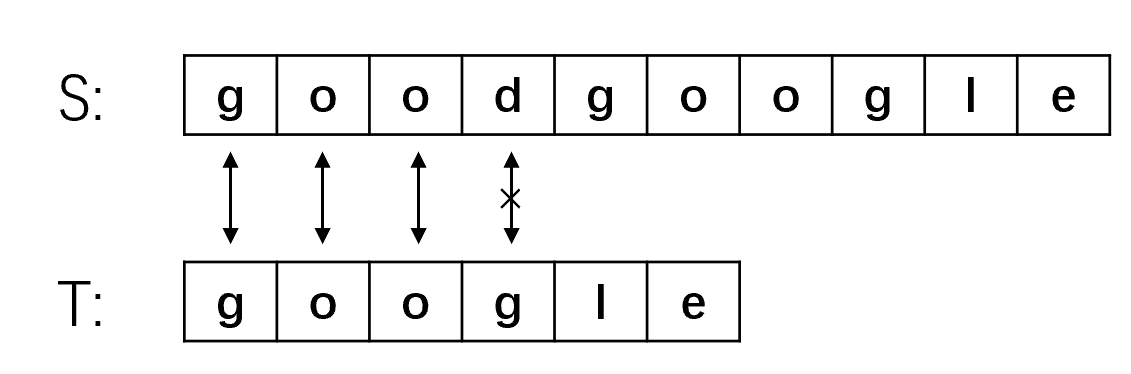
(2) 主串S从第二位开始于子串T匹配,第一步就匹配失败,将主串指针指向第三位S[2],子串指针指向开头,继续匹配。
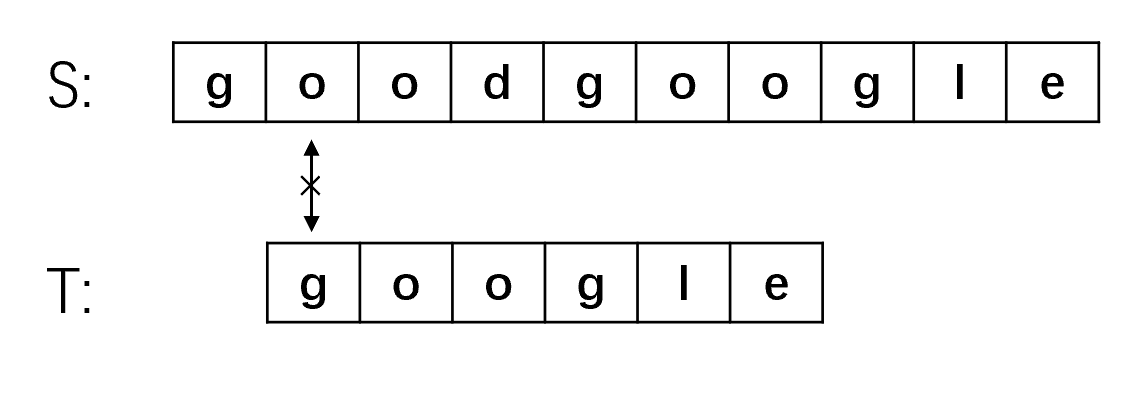
(3) 同步骤二,第一步就匹配失败,将主串指针移动到第四位S[3],子串指针指向开头,继续匹配。
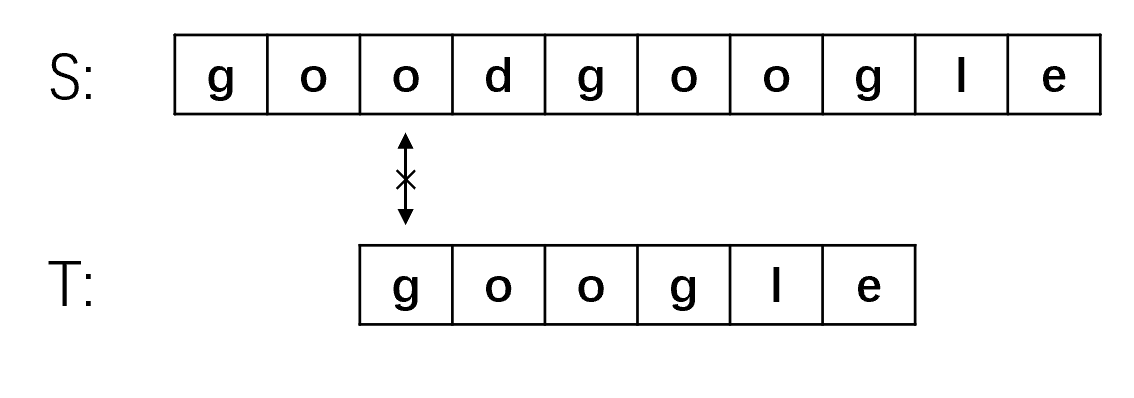
(4) 还是第一步就匹配失败,将主串指针移动到第五位S[4],子串指针指向开头,继续匹配。
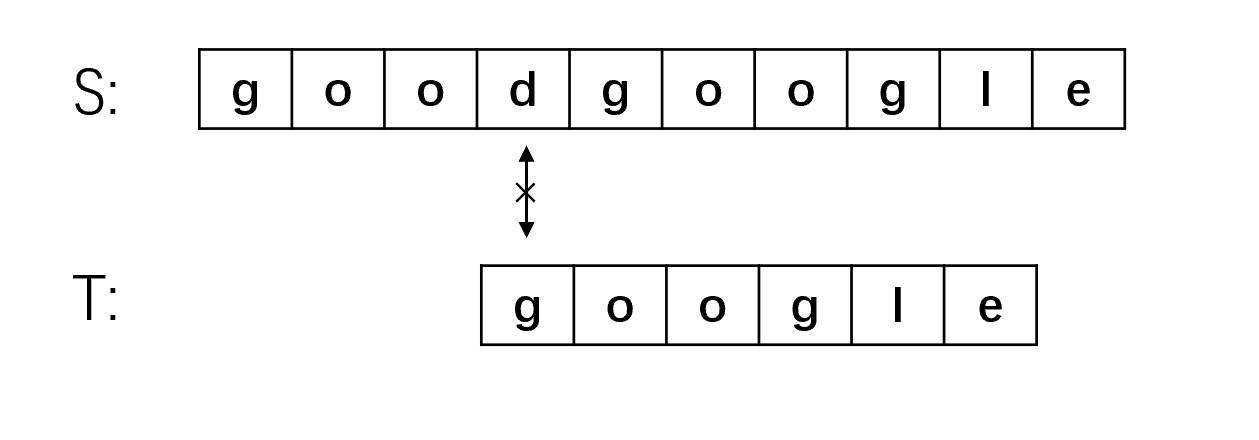
(5) 到步骤5终于第一步能够匹配上,从S[4]开始指针依次向后移动,六个字母全部匹配上,匹配成功!
根据上面的步骤,我们可以得出朴素模式匹配算法的代码如下所示:
int find_sub_string(string s, string t)
{
int i = 0, j = 0; //初始化两个指针
while(i
if(s[i] == t[j]){
i++; //如果两个指针指向的字符相等
j++; //则将两个指针向后移动
}
else{
i = i - j + 1; //匹配失败,i退回到上次匹配首位的下一位
j = 0; //j退回到子串首位
}
}
if(j=t.size()){ //j走到子串末尾说明匹配成功
return i - j; //匹配成功返回主串中子串出现的第一位
}
else
return -1; //匹配失败,返回-1
}
int j = 0;
next[0] = 0; //初始化
for(int i = 1; i //i指针指向的是后缀末尾,j指针指向的是前缀末尾
while(j0&&s[i]!=s[j]) j = next[j-1]; //前后缀不相同,去找j前一位的最长相等前后缀
if(s[i]==s[j]) j++; //前后缀相同,j指针后移
next[i] = j; //更新next数组
}
}
if(t.size()==0) return 0;
get_Next(t, next);
int j = 0;
for(int i = 0; i
下面我们来做一道例题进行巩固。
KMP例题

这是ACwing题库中的831题
用刚刚给出的代码模板可以得出这道题的代码如下:
#include
#include
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
int ne[N];
string s, p;
void get_Next(string s, int ne[]) //这个函数对字符串s进行预处理得到next数组
{
int j = 0;
ne[0] = 0; //初始化
for (int i = 1; i 0 && s[i] != s[j]) j = ne[j - 1]; //前后缀不相同,去找j前一位的最长相等前后缀
if (s[i] == s[j]) j++; //前后缀相同,j指针后移
ne[i] = j; //更新next数组
}
}
int main()
{
cin >> n >> p >> m >> s;
get_Next(p, ne);
for (int i = 0, j = 0; i 0 && s[i] != p[j]) j = ne[j - 1];
if (s[i] == p[j]) j++;
if (j == n) {
cout 








