人工智能笔记（第二集）-慈云数据

参考视频：(强推|双字)2022吴恩达机器学习Deeplearning.ai课程_哔哩哔哩_bilibili p43-p74

本文对视频做了一些补充，参考书：Neural Networks and Deep Learning邱锡鹏

一.神经网络

应用领域：语音识别，计算机视觉，自然语言处理（NLP）。

1.1神经元

神经网络是由神经元构成的，神经元的的结构如下：

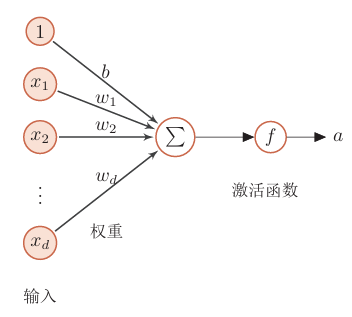
可以有多个输入，每个输入有不同的权重。上图左边的部分相加相当于

1.1.1激活函数

激活函数f有很多种，Sigmoid函数就是一种常见的激活函数。

激活函数的性质:

1. 连续并可导（允许少数点上不可导）的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。

2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。

3. 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

经过激活函数之后，输出就变为

如果使用sigmoid函数作为激活函数，g的表达式如下：

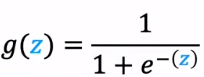
下面介绍几种激活函数

1.1.1.1sigmoid型函数

这个函数在上文中已经提过，就不进行扩展了。

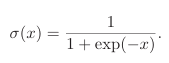
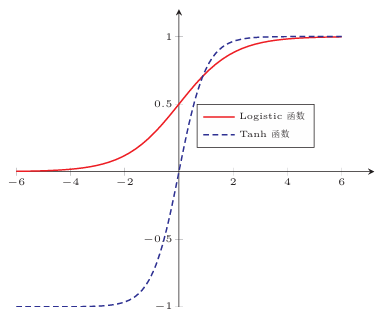
1.1.1.2Tanh函数

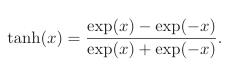
这个函数类似sigmoid函数，值域是(-1,1)。

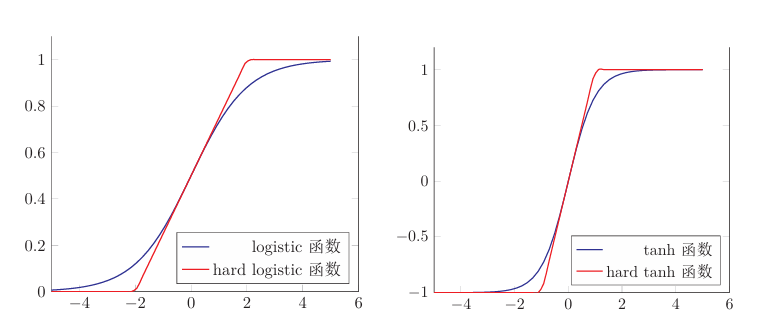
1.1.1.3Hard-Logistic和Hard-Tanh函数

使用分段函数来近似表示logistic(sigmoid)和Tanh。

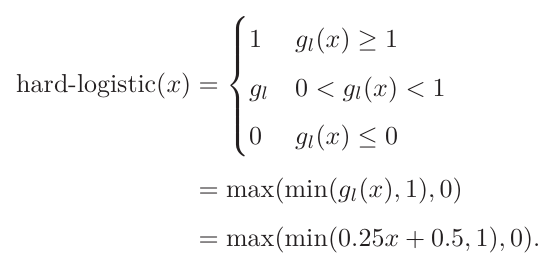
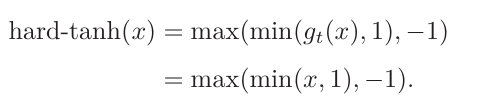
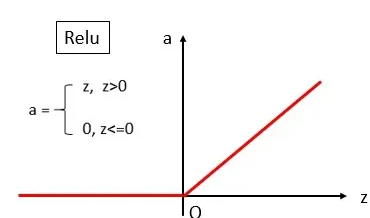
1.1.1.4修正线性单元（ReLU）

这个函数很简单，只是一个斜坡，但是如今最常用。

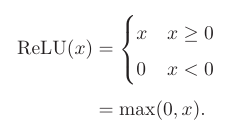
但是有很多优点：

1.计算简单高效。

2.缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。

3.ReLu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

但是这就出现了一个问题，如果输入不是正数，那输出就为0。那么这样的神经元就相当于“死掉”了。ReLU会造成很多神经元的死亡。这样的好处就是，让没什么用的特征无法传播，从而使网络可以“聚焦”在有用的特征上面。

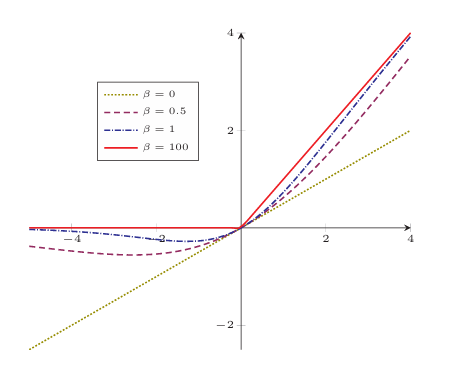
1.1.1.5Swish函数

这个函数通过 $\beta$ 控制，介于ReLU和线性之间。

1.1.2选择激活函数

如果是二分问题（输出只有0和1），选择sigmoid函数。

回归问题，需要看输出的取值范围。如果范围是非负，那就用ReLU，如果是实数集，那就用线性的激活函数（只是在输入乘以一个常数）。

1.2神经网络

多个神经元可以构成神经网络。

神经网络示意图如下：

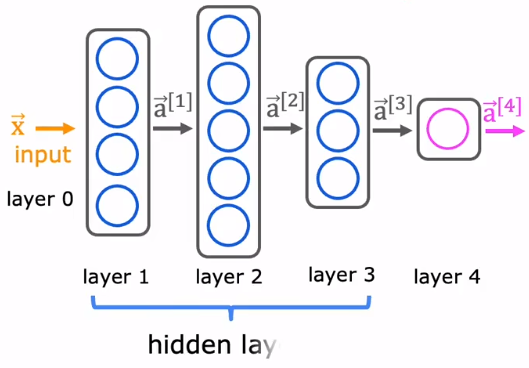
每一个神经元都会输出一个a，那么一层的神经元就会输出一个 $\vec{a}$ 。

1.2.1前馈网络

每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层叫输入层，最后一层叫输出层，其它中间层叫做隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播。

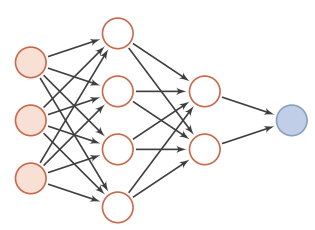
1.2.2反馈网络

反馈网络中神经元不但可以接收其它神经元的信号，也可以接收自己的反馈信号。和前馈网络相比，反馈网络中的神经元具有记忆功能，在不同的时刻具有不同的状态。反馈神经网络中的信息传播可以是单向或双向传递，因此可用一个有向循环图或无向图来表示。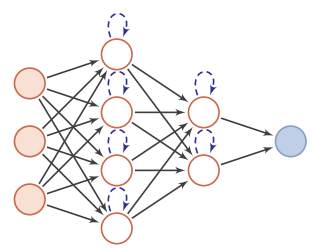

二.多分类问题

多类分类（ Multi-class Classification ）问题是指分类的类别数 C 大于 2 。

多个参数的分类公式就会变成这样

loss就会变成这样：

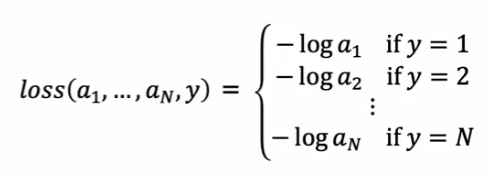
三.卷积神经网络

3.1卷积

一维卷积：假设一个信号发生器每个时刻t产生一个信号xt，其信息的衰减率为wk，即在k − 1个时

间步长后，信息为原来的 w k 倍。假设滤波器长度为 m ，它和一个信号序列 x 1 , x 2 , · · · 的卷积为：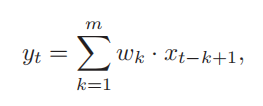

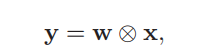信号序列 x 和滤波器 w 的卷积定义为

其中⊗表示卷积运算。

二维卷积：

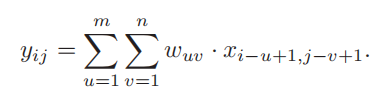
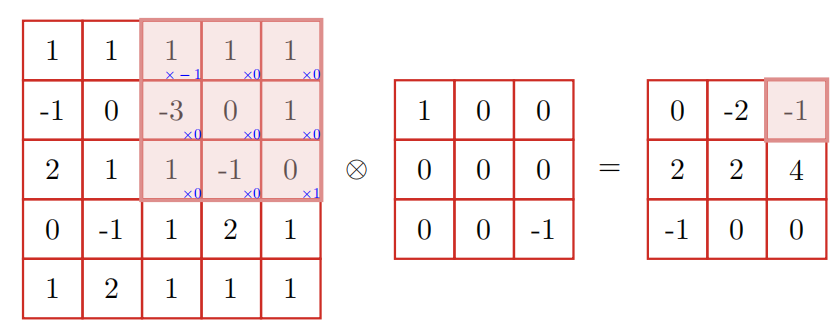
和一维的很像，不过可以通过自己设置滤波器来达到不同的效果。

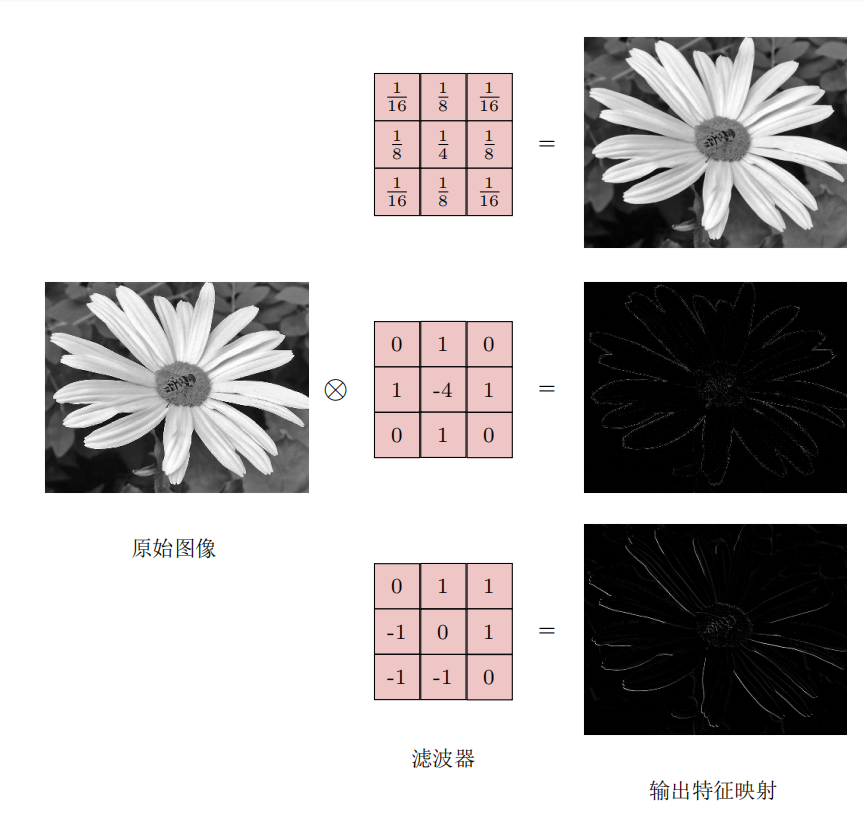
书上写的实在不好理解，可以看这篇文章参考：

https://www.zhihu.com/question/22298352

3.2卷积神经网络

如果采用卷积来代替全连接，第 l 层的净输入 z ( l ) 为第 l − 1 层活性值 a ( l − 1)和滤波器w ( l ) ∈ R m 的卷积，即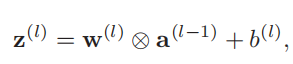

其中滤波器 w ( l ) 为可学习的权重向量， b ( l ) 为可学习的偏置。

一个卷积神经网络主要由以下5层组成：

数据输入层/ Input layer
卷积计算层/ CONV layer
ReLU激励层 / ReLU layer
池化层 / Pooling layer
全连接层 / FC layer 卷积层的作用是提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器。
使用卷积神经网络之后，卷积层之间的连接会大大减少，每一个神经元只和前一层的几个临近的神经元有关系。并且同一层的神经元的权重是相同的，即共用同一个滤波器W。

池化层夹在连续的卷积层中间，用于压缩数据和参数的量，减小过拟合。简而言之，如果输入是图像的话，那么池化层的最主要作用就是压缩图像。

池化层用的方法有Max pooling 和 average pooling，而实际用的较多的是Max pooling。就是选出窗口里面最大的一个值

书中给了一个例子：

1. 输入层， 224 × 224 × 3 的图像； 2. 第一个卷积层，使用两个 11 × 11 × 3 × 48 的卷积核，步长 s = 4 ，零填充 p = 3 ，得到两个 55 × 55 × 48 的特征映射组。 3. 第一个池化层，使用大小为 3 × 3 的最大汇聚操作，步长 s = 2 ，得到两个27 × 27 × 48 的特征映射组。 4. 第二个卷积层，使用两个 5 × 5 × 48 × 128 的卷积核，步长 s = 1 ，零填充 p = 1 ，得到两个 27 × 27 × 128 的特征映射组。 5. 第二个池化层，使用大小为3 × 3 的最大汇聚操作，步长 s = 2 ，得到两个13 × 13 × 128 的特征映射组。 6. 第三个卷积层为两个路径的融合，使用一个 3 × 3 × 256 × 384 的卷积核，步长s = 1 ，零填充 p = 1 ，得到两个 13 × 13 × 192 的特征映射组。 7. 第四个卷积层，使用两个 3 × 3 × 192 × 192 的卷积核，步长 s = 1 ，零填充p = 1 ，得到两个 13 × 13 × 192 的特征映射组。 8. 第五个卷积层，使用两个 3 × 3 × 192 × 128 的卷积核，步长 s = 1 ，零填充p = 1 ，得到两个 13 × 13 × 128 的特征映射组。 9. 池化层，使用大小为3 × 3 的最大汇聚操作，步长 s = 2 ，得到两个 6 × 6 × 128的特征映射组。 10. 三个全连接层，神经元数量分别为 4096 ， 4096 和 1000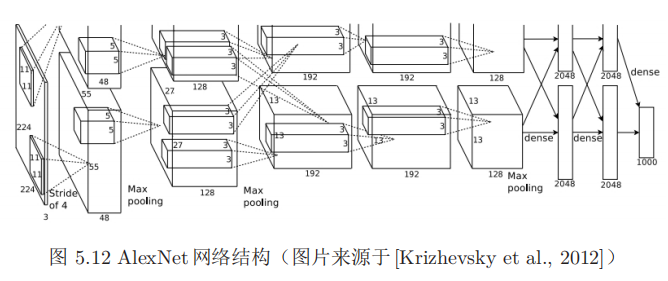
四.循环神经网络
循环神经网络（ Recurrent Neural Network ， RNN ）是一类具有短期记忆能力的神经网络。在循环神经网络中，神经元不但可以接受其它神经元的信息，也可以接受自身的信息，形成具有环路的网络结构。这种神经网络可以处理具有时序的数据，比如预测下一句话，预测明天的股价。
4.1简单的循环网络

一个输入，一个输出，一个隐藏层神经元。
假设在时刻 t 时，网络的输入为 $x_{t}$ ，隐藏层状态（即隐藏层神经元活性值）为 $h_{t}$ 不仅和当前时刻的输入 $x_{t}$ 相关，也和上一个时刻的隐藏层状态 $h_{t-1}$ 相关。表达式如下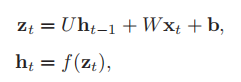：按时间展开的样子：
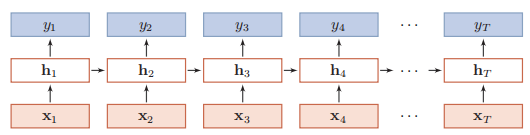
4.2RNN在机器学习中的应用

4.2.1序列到类别模式
序列到类别模式主要用于序列数据的分类问题：输入为序列，输出为类别。比如在文本分类中，输入数据为单词的序列，输出为该文本的类别。按照时间序列进行输入，经过T个时刻之后完成输入。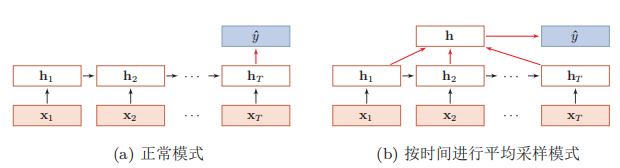有两种输出模式，只使用 $h_{t}$ 作为特征，和综合每一个时刻的h作为特征。
4.2.2同步的序列到序列模式
同步的序列到序列模式主要用于序列标注（ Sequence Labeling ）任务，即每一时刻都有输入和输出，输入序列和输出序列的长度相同。比如词性标注（ Part-of-Speech Tagging）中，每一个单词都需要标注其对应的词性标签。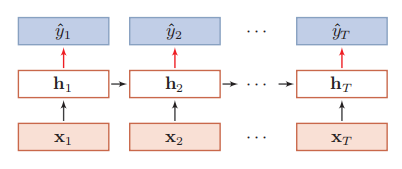
4.2.3异步的序列到序列模式
异步的序列到序列模式也称为编码器 - 解码器（ Encoder-Decoder ）模型，即输入序列和输出序列不需要有严格的对应关系，也不需要保持相同的长度。
应用的范围非常广泛，比如：机器翻译，文本摘要，阅读理解，语音识别。
在异步的序列到序列模式中（如图 6.5 所示），输入为一个长度为 T 的序列 x 1: T = ( x 1 , · · · , x T ) ，输出为长度为 M 的序列 y 1: M = ( y 1 , · · · , y M ) 。经常通过先编码后解码的方式来实现。先将样本x 按不同时刻输入到一个循环神经网络（编码器）中，并得到其编码h T 。然后在使用另一个循环神经网络（解码器）中，得到输出序列y ˆ 1: M 。为了建立输出序列之间的依赖关系，在解码器中通常使用非线性的自回归模型。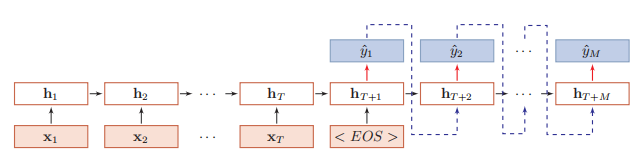
4.3基于门控的循环神经网络

4.3.1长短期记忆网络
长短期记忆（ Long Short-Term Memory ， LSTM ）网络是循环神经网络的一个变体，可以有效地解决简单循环神经网络的梯度爆炸或消失问题。
普通的RNN只有一个隐藏层,这样很难控制梯度。LSTM加入了一个C层，并且通过三个门来控制是否将信息保留，以及传递什么信息到下一个时刻。

LSTM 网络中三个门的作用为遗忘门 f t 控制上一个时刻的内部状态 c t − 1 需要遗忘多少信息。输入门 i t 控制当前时刻的候选状态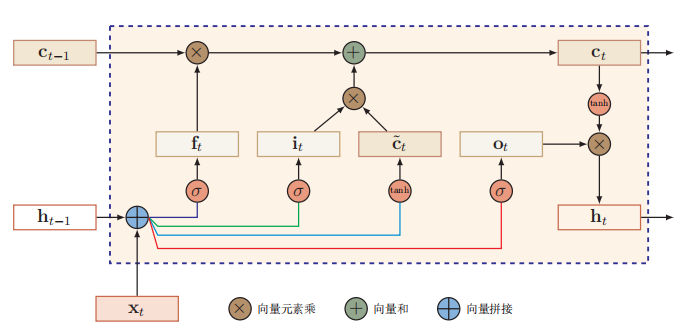 $\widetilde{c_{t}}$ 有多少信息需要保存。输出门 o t 控制当前时刻的内部状态 c t 有多少信息需要输出给外部状态 h t 。
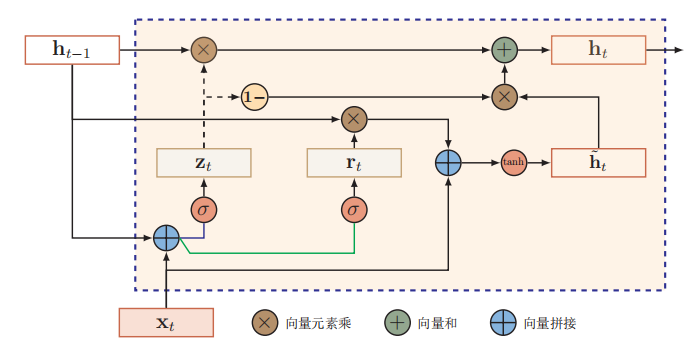
4.3.2门控循环单元
门控循环单元（ Gated Recurrent Unit ， GRU）网络是一种比 LSTM 网络更加简单的循环神经网络。 GRU将输入门与和遗忘门合并成一个门：更新门。同时， GRU 也不引入额外的记忆单元，直接在当前状态 h t 和历史状态 h t − 1 之间引入线性依赖关系。