无监督学习也称为无监督机器学习,是机器学习领域中的重要分支之一,它使用机器学习算法来分析未标记的数据集并进行聚类。
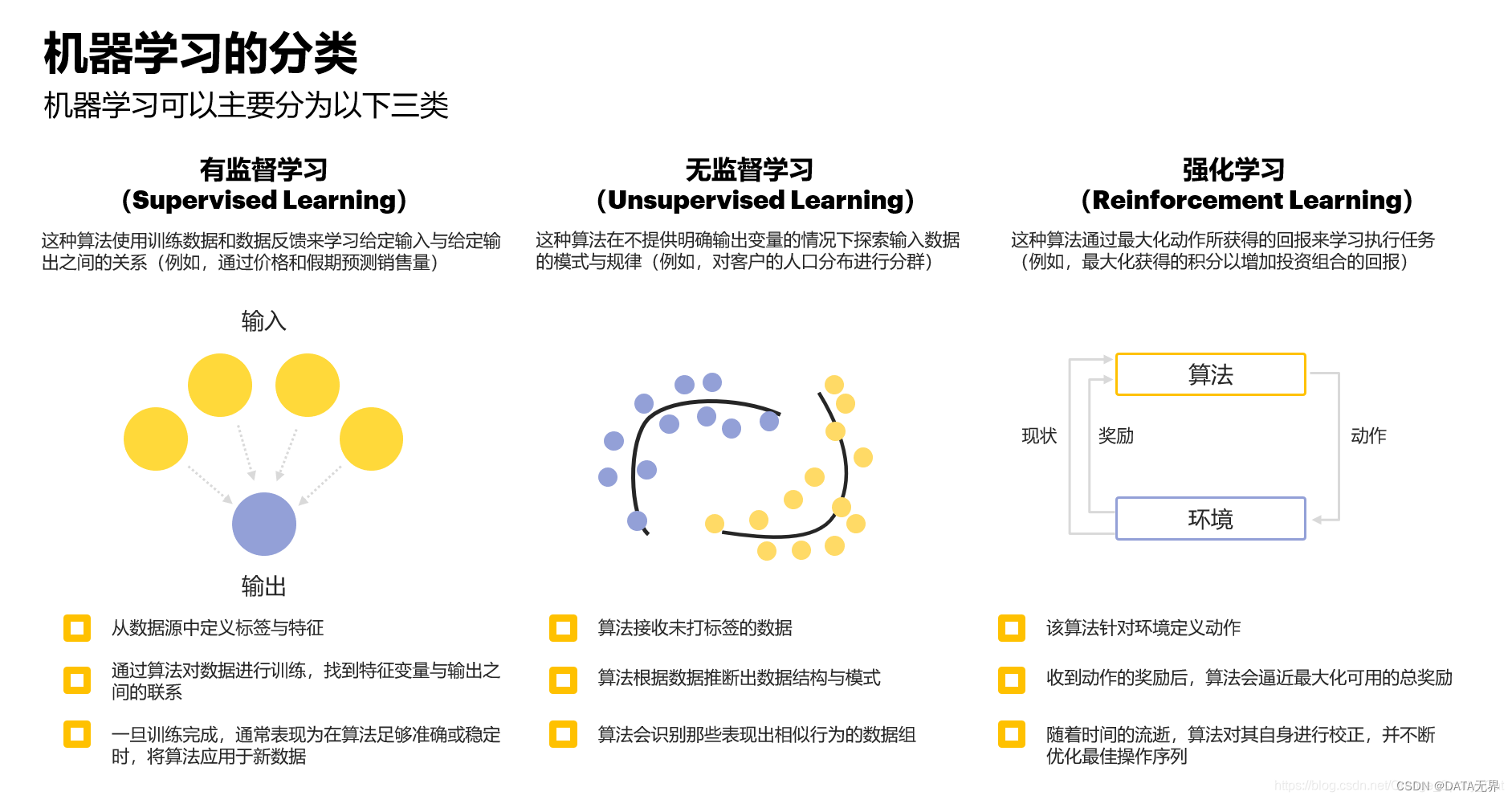
与有监督学习和强化学习不同,无监督学习的数据集中不包含任何人工标注的目标值或反馈信号。
无监督学习算法需要从原始数据中自主发现内在结构、模式或知识。这种“自主学习”的范式更贴近人类自主学习的方式,使得无监督学习在许多应用场景都有独特的优势,这种方法能够发现信息的相似性和差异性,因而是探索性数据分析、交叉销售策略、客户细分和图像识别的理想解决方案。
1. 无监督学习的原理
无监督学习的核心思想是通过对数据的统计特征、相似度等进行分析和挖掘,利用密度估计、聚类和降维等技术来捕获和发现数据隐藏的内在结构和模式。
无监督学习的主要原理可以概括为:

密度估计(Density Estimation)
密度估计是无监督学习的一个基本问题。它旨在估计样本数据的概率密度函数,从而刻画数据的整体分布特征。常用的密度估计方法包括核密度估计、高斯混合模型、K-近邻等。掌握了数据分布,就能发现异常数据点、检测新观测值等。
聚类(Clustering)
聚类是将数据集中的样本划分为若干个类别的过程,使得同一类别内的样本相似度较高,不同类别之间的样本相似度较低。在聚类过程中,每个样本点都被视为一个向量,聚类算法通过计算样本之间的距离或相似度,将相似的样本归为同一类别。常见的聚类算法包括K均值聚类、层次聚类、DBSCAN、高斯混合模型等。聚类分析有助于发现数据的内在组织结构。
降维(Dimensionality Reduction)
数据常常存在维度灾难的问题,即特征空间过高导致计算复杂度和数据稀疏性增加。降维技术通过数学上的投影等方式将高维数据映射到一个低维空间,在减少数据的维度的同时保留数据的原始结构和特征关系,从而简化后续处理。主成分分析(PCA)、t-SNE等都是常用的无监督降维方法。
表示学习(Representation Learning)
表示学习旨在从原始数据中自动学习出良好的特征表示,使得表示空间中相似的样本更易于被区分和聚类。自编码器(AutoEncoder)就是一种常用的无监督神经网络模型,能够有效地学习出高质量的数据表示。
无监督学习算法通常会以无约束或少量约束的方式优化某些目标函数,如最大化数据对数似然、最小化重构误差等,从而捕获数据的本质结构和模式。得益于深度学习技术的发展,无监督表示学习逐渐成为研究的热点。
2. 无监督学习的常用核心算法
2.1. K-Means聚类算法(K均值聚类)
K-Means是最常用和最简单的聚类算法之一,它是一种基于中心点的聚类方法,它将样本分配给离其最近的K个中心点所对应的簇。该算法的核心步骤包括初始化中心点、分配样本到最近的中心点所在的簇、更新中心点位置,使得簇内样本间的平方和最小。K均值聚类适用于数据集中各个簇的形状近似球形、大小相似的情况。
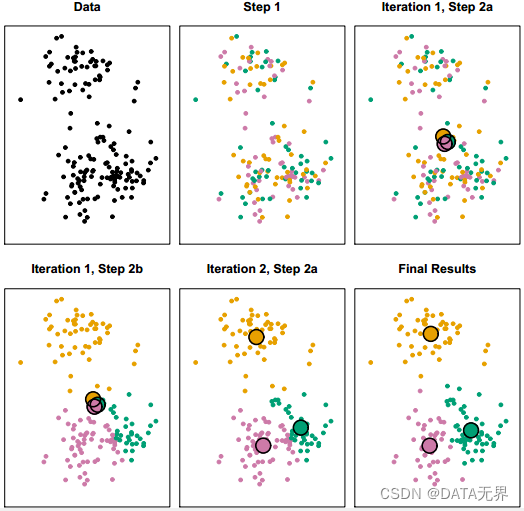
一般算法步骤如下:
- 随机初始化k个聚类中心
- 重复以下步骤直到收敛:
- 将每个样本分配到与之最近的聚类中心
- 重新计算每个簇的聚类中心
K-Means具有简单高效的优点,但也存在一些缺陷,如对噪声和异常值敏感、需要预先指定簇数k等。
2.2 层次聚类算法
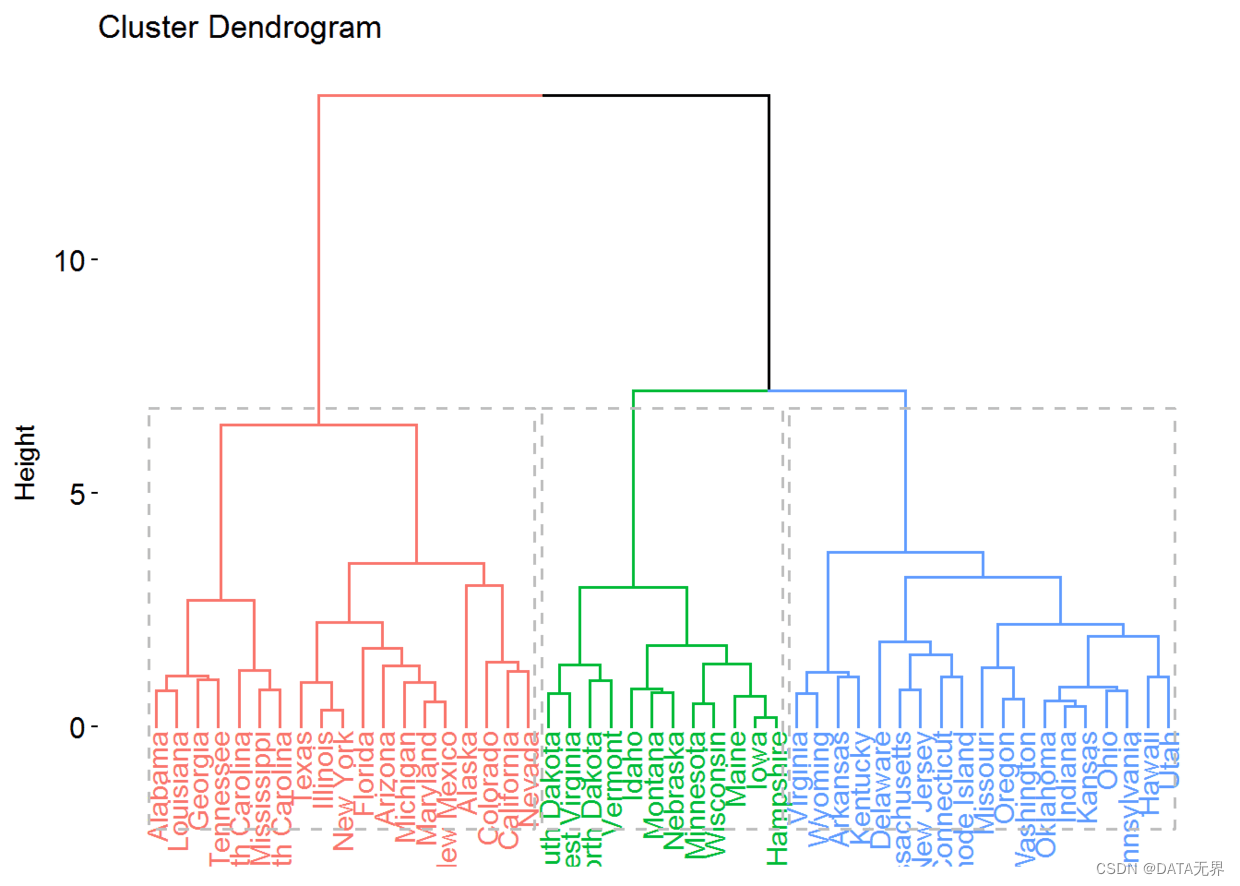
层次聚类算法通过逐步合并或分裂簇来构建一个层次化的聚类树状结构。主要分为两种策略:
- 凝聚层次聚类(底至顶):从每个样本作为一个簇开始,逐步合并最相似的簇
- 分裂层次聚类(顶至底):从所有样本作为一个簇开始,逐步将离散程度最高的簇进行分裂
常用的相似性度量包括最小距离、最大距离、平均距离等。需要事先确定一个合理的terminated条件来决定最终的聚类数目。
2.3. 高斯混合模型(GMM)

GMM假设整个数据服从一个由多个高斯分布混合而成的概率分布模型。可以使用期望最大化(EM)算法来估计每个高斯分布的参数(均值、协方差)和所占的混合权重。模型估计完成后,每个样本可以基于后验概率被"软分配"到不同的高斯分布中。GMM广泛应用于聚类、密度估计等任务。
2.4. 主成分分析(PCA)
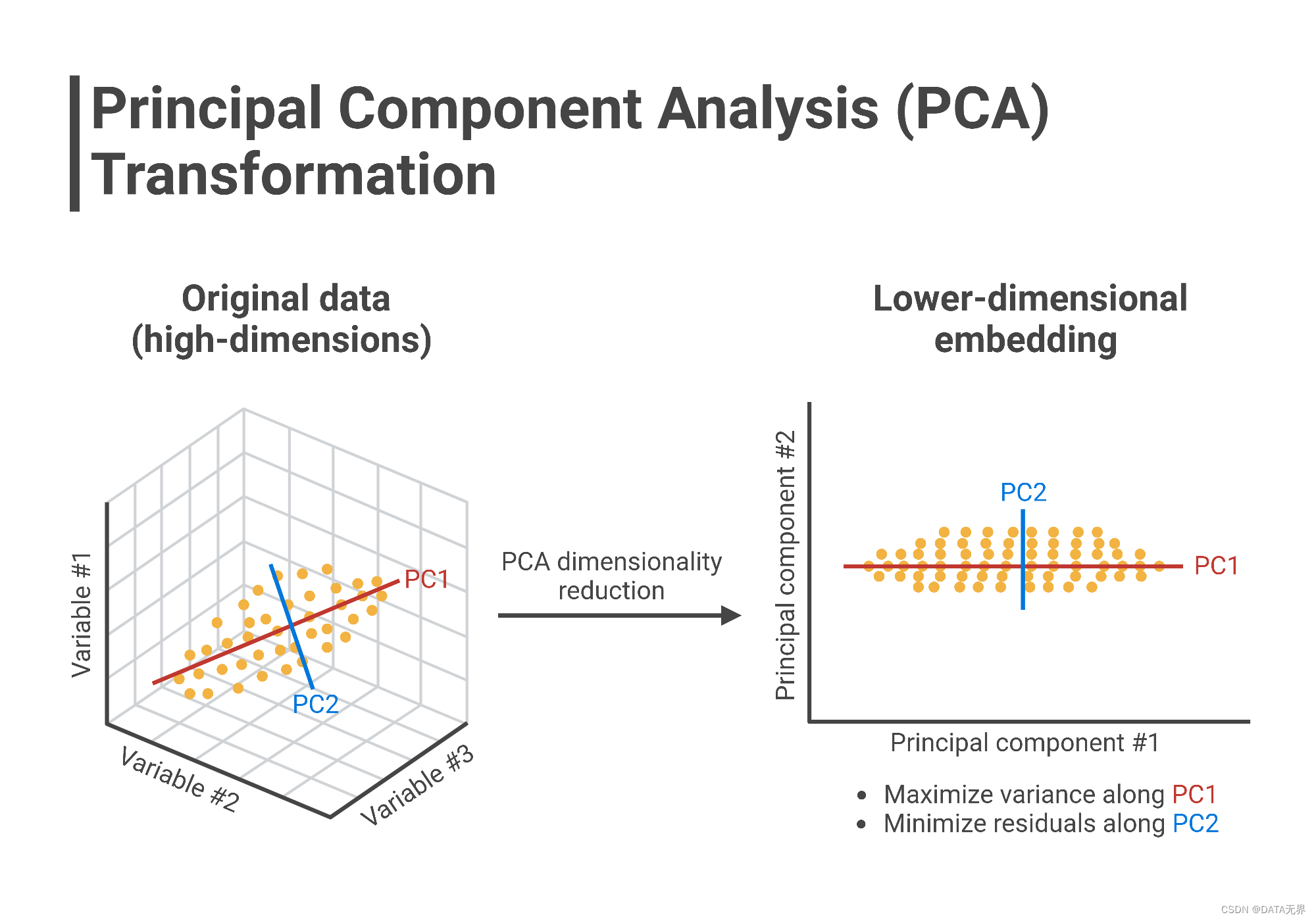
PCA是一种常用的无监督降维和数据表示技术。其主要思想是将原始数据通过线性变换投影到一组相互正交的低维空间中,使得投影后数据的方差最大化。PCA的主要思想是找到数据中最主要的特征,即主成分,以降低数据的维度。具体步骤包括:中心化数据、计算协方差矩阵、求解特征值和特征向量、选取方差贡献度最大的前k个主成分等。PCA常被用于数据可视化、压缩和特征提取的预处理步骤。
2.5. t-SNE
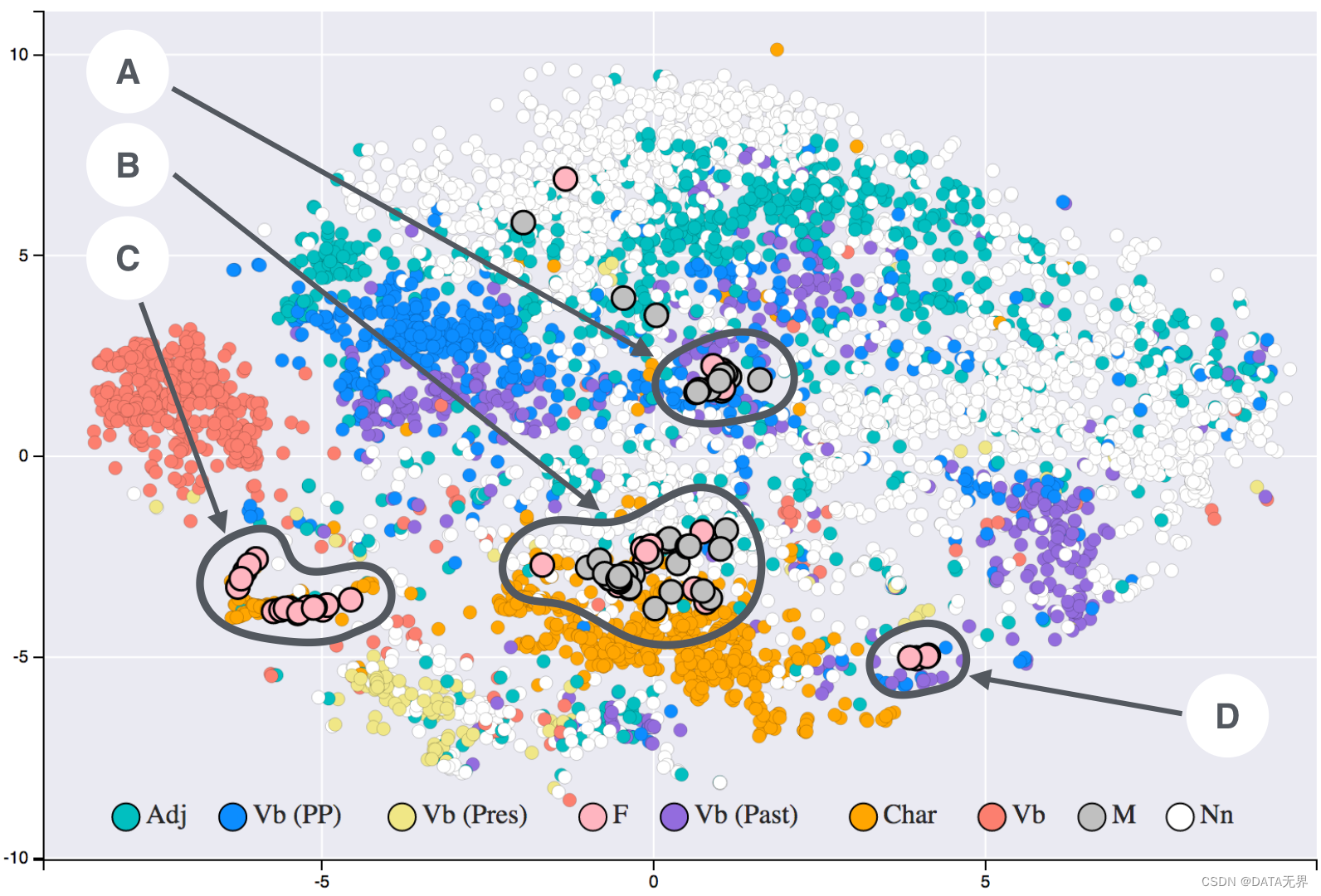
t-SNE(t-分布随机邻域嵌入)是一种较新的非线性降维技术,能够有效地保留原始高维数据的局部邻域结构。首先计算高维空间样本之间的相似度,然后在低维空间中最小化相似度与映射后距离之间的KL散度。t-SNE常用于可视化高维数据,辅助探索数据的内在分布和聚类结构。
2.6. 自编码器(AutoEncoder)
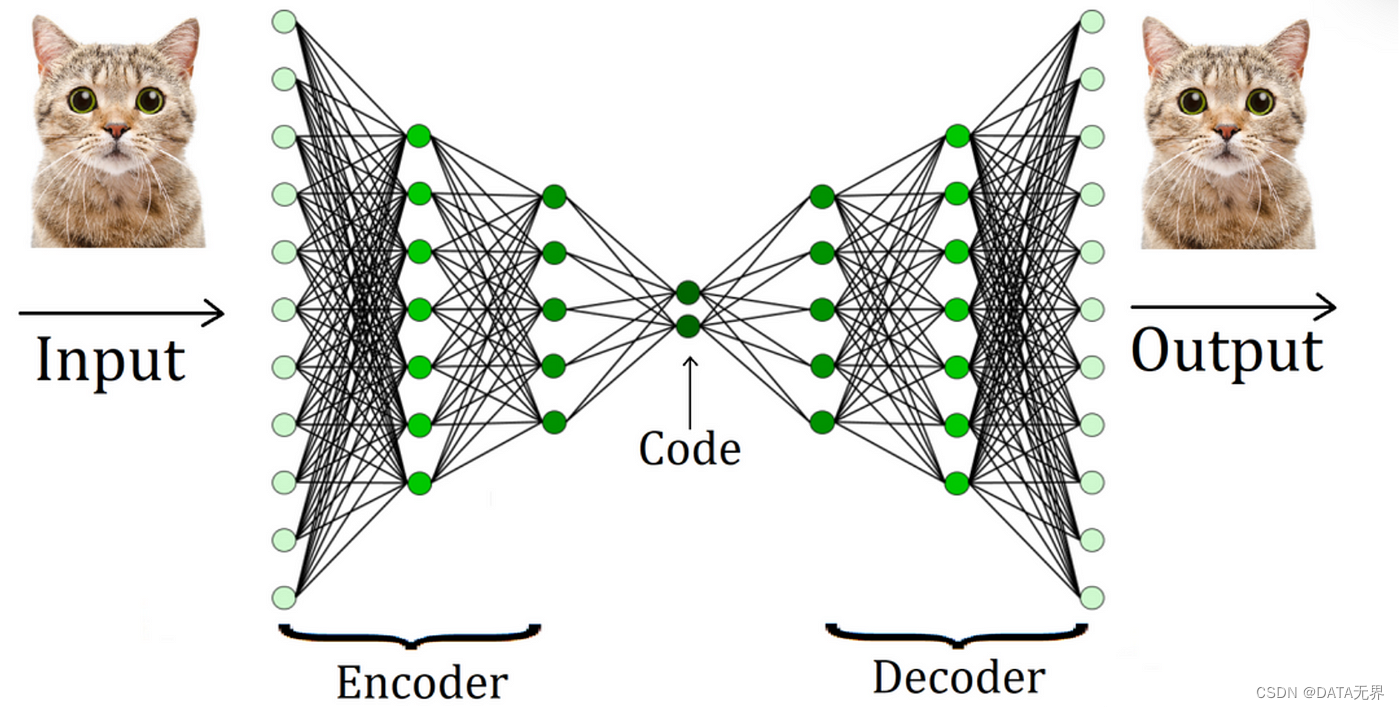
自编码器是一种基于人工神经网络的无监督表示学习模型。其由编码器和解码器组成,编码器将输入数据映射到隐含层的低维表示,解码器则试图重构原始输入。通过最小化输入和重构之间的损失函数,自编码器能够自动学习出对应问题的良好特征表示。堆叠自编码器、变分自编码器等都是基于这一思想的扩展。
3. 无监督学习的实现
3.1 K均值聚类的实现
下面我们通过一个基于Python的K-Means聚类算法实例,来更直观地理解无监督学习。
import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn.datasets import make_blobs # 生成样本数据 X, y = make_blobs(n_samples=500, centers=4, n_features=2, random_state=0) # 初始化K-Means模型 kmeans = KMeans(n_clusters=4, random_state=0) # 训练K-Means模型 kmeans.fit(X) # 预测每个样本的簇标签 labels = kmeans.predict(X) # 可视化结果 plt.figure(figsize=(8, 6)) plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis') plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1], marker='x', c='red', s=100) plt.title('K-Means Clustering') plt.xlabel('Feature 1') plt.ylabel('Feature 2') plt.show()这段代码首先使用make_blobs函数生成一个包含500个样本的数据集X和y。这些样本被划分为4个不同的簇,每个样本有2个特征。
接下来,我们初始化一个KMeans对象,将聚类数n_clusters设置为4。random_state参数用于控制随机种子,确保每次运行结果一致。
调用fit方法使用X训练K-Means模型。模型会迭代调整聚类中心的位置,最小化簇内样本到中心的平方距离之和。
使用predict方法为每个样本预测一个簇标签。
最后,我们使用Matplotlib绘制可视化结果。通过plt.scatter函数绘制样本点,不同颜色代表不同的簇。plt.scatter的第二次调用绘制聚类中心,使用红色加号标记。
设置图像标题、x轴和y轴标签,完成可视化。
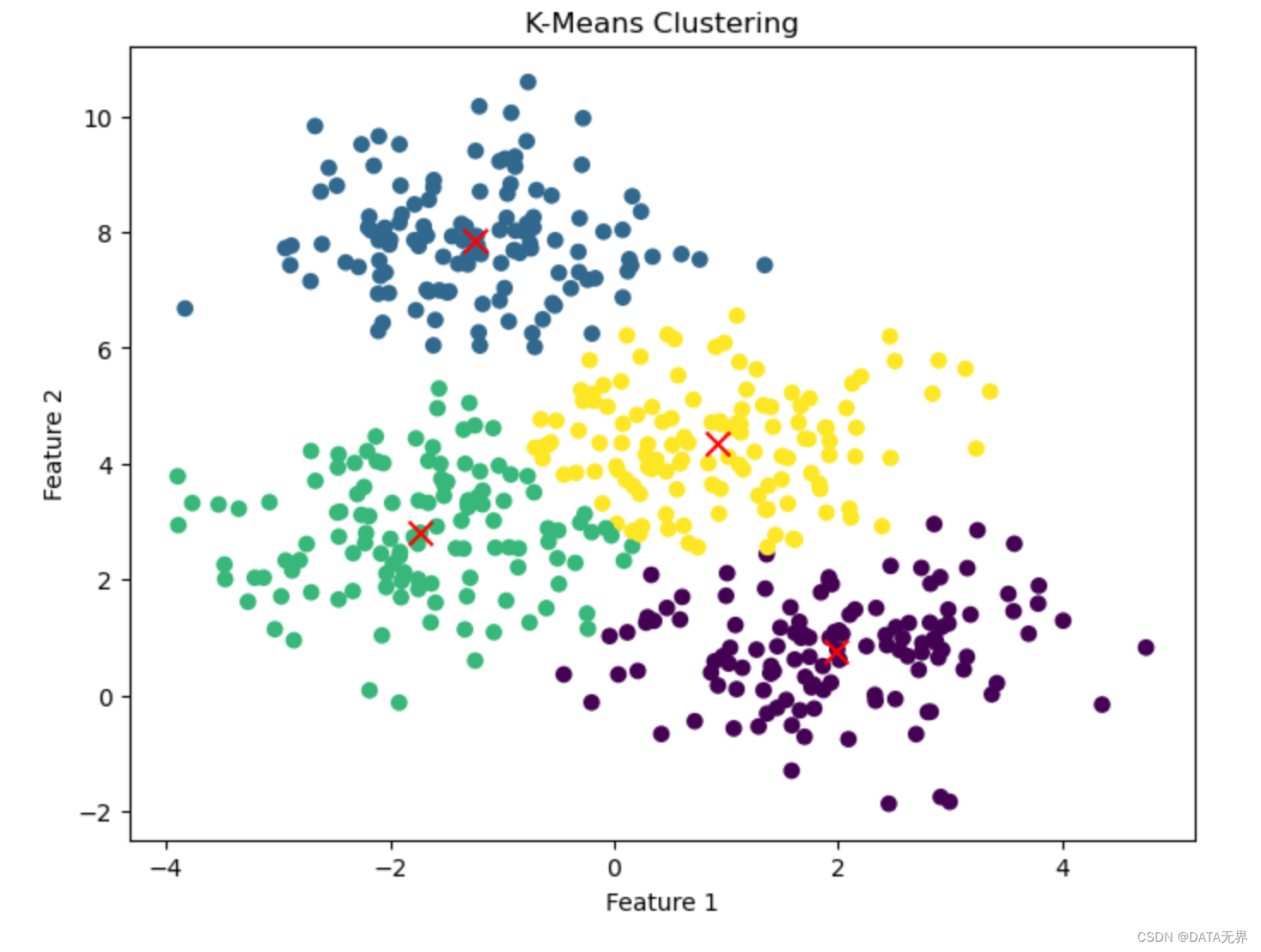
我们在 Jupyter Notebook 环境中运行上述代码后,可以看到一个可视化的2维散点图,展示了K-Means在这个人工数据集上的聚类效果。不同颜色的点代表属于不同簇的样本,红色加号标记表示估计出的4个聚类中心。
从图中还可以看到,K-Means算法能够较好地将数据划分为4个紧密的簇。但是,由于数据分布并不是严格球形,有一些样本仍被错误分类到其他簇中。这也体现了K-Means对初始中心选择和数据分布假设的敏感性。
K-Means聚类算法通过优化某些目标函数,比如最小化聚类内的方差,从而将相似的样本聚集到同一个簇中,算法会迭代地调整聚类中心的位置,使每个样本与离它最近的中心之间的平方距离之和最小化。
3.2 层次聚类的实现
我们将使用SciPy库中的层次聚类模块,实现一个基于Ward’s最小方差准则的聚类算法。该算法采取自底向上的策略,初始时将每个样本作为一个单独的簇,然后在每一步中合并两个最相近的簇,直到所有样本聚合为一个簇或满足指定的终止条件。
import numpy as np from sklearn.datasets import load_iris from sklearn.cluster import AgglomerativeClustering import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # 加载鸢尾花数据集 iris = load_iris() X = iris.data # 初始化层次聚类模型 clustering = AgglomerativeClustering(n_clusters=3, linkage='ward') # 训练模型 clustering.fit(X) # 获取样本的聚类标签 labels = clustering.labels_ # 可视化结果 fig = plt.figure(figsize=(8, 6)) ax = fig.add_subplot(111, projection='3d') # 设置不同颜色表示不同簇 colors = ['r', 'g', 'b'] # 绘制每个簇的样本点 for label, color in zip(set(labels), colors): data = X[labels == label] ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=color, label=f'Cluster {label+1}') # 设置图例、坐标轴标签和标题 ax.legend() ax.set_xlabel('Sepal Length') ax.set_ylabel('Sepal Width') ax.set_zlabel('Petal Length') ax.set_title('Hierarchical Clustering on Iris Dataset') # 调整视角角度 ax.view_init(30, 30) plt.show()这段代码首先使用从scikit-learn库中加载鸢尾花数据集iris。该数据集包含150个样本,每个样本有4个特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。

接下来,我们初始化AgglomerativeClustering类,使用Ward’s最小方差准则作为链接标准,并设置簇数为3。
调用fit方法在数据X上训练层次聚类模型。该算法会自底向上地将相似的样本合并为簇。
从模型中获取每个样本的聚类标签labels。
使用Matplotlib创建一个3D图像,并添加一个3D子图。
设置不同的颜色表示不同的簇。
遍历每个簇的样本点,使用ax.scatter在3D图中绘制,同一簇的样本使用相同颜色。
设置图例、坐标轴标签和标题。
调用ax.view_init(30, 30)调整3D图像的视角角度,使其更加容易观察。
最后调用plt.show()展示可视化结果。
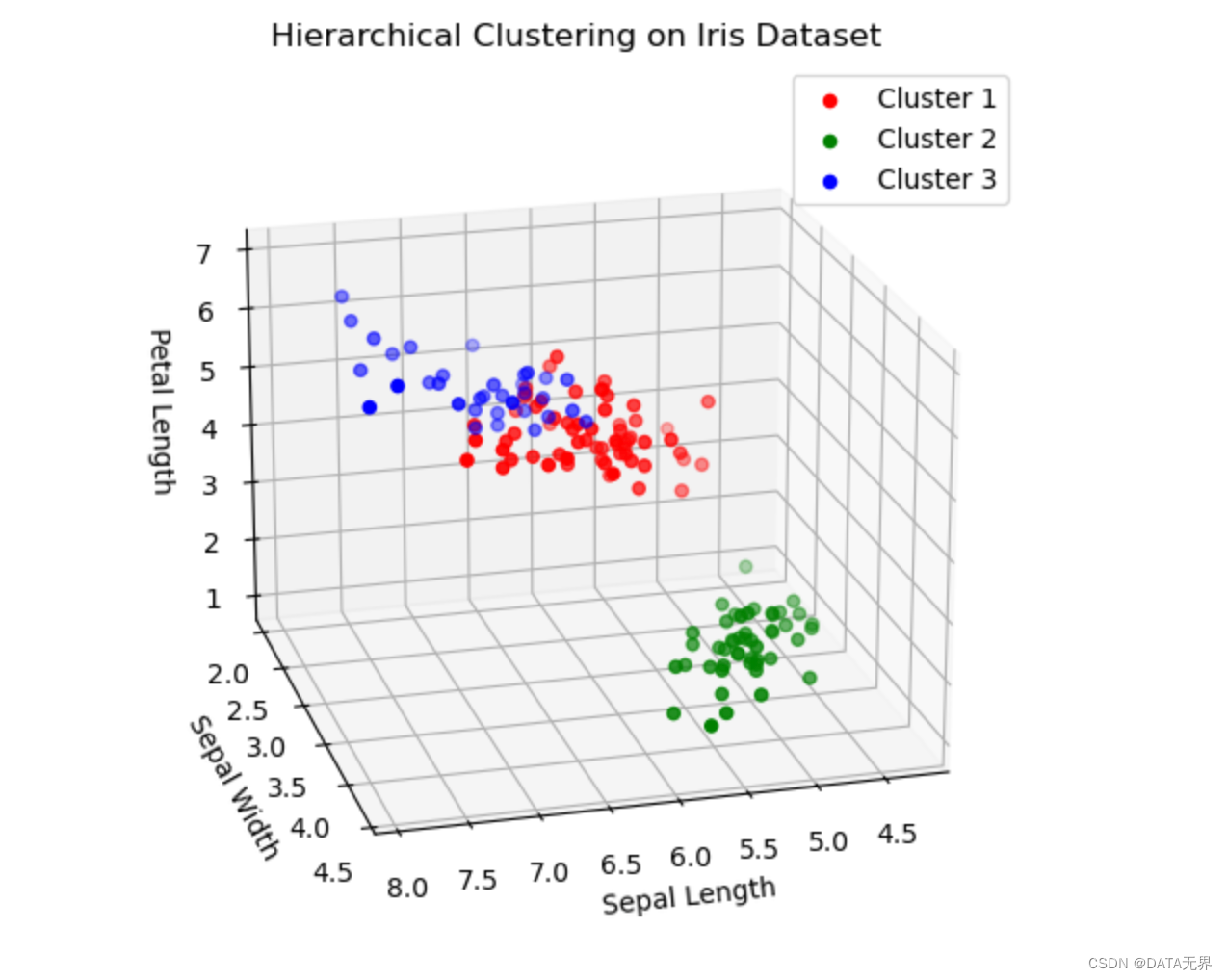
运行上述代码后,我们将看到一个3D散点图,展示了层次聚类算法在鸢尾花数据集上的聚类效果。不同颜色的点代表属于不同簇的样本。从图中我们可以直观地看到,层次聚类算法能较好地将鸢尾花数据集划分为3个簇,每个簇对应一种鸢尾花品种。
层次聚类的主要优势在于能够很直观地呈现数据的层次结构,同时不需要预先指定聚类数目。
但它也存在一些缺点,比如对于大规模数据计算复杂度较高,一旦发生错误合并也无法回退等。总的来说,层次聚类是一种解释性很强且实用的无监督学习算法。
3.3 高斯混合模型(GMM)的实现
我们使用Python中的scikit-learn库,通过一个1000个样本的示例,来详细说明高斯混合模型(GMM)算法的原理和实现。
GMM是一种基于概率模型的无监督学习算法,它假设整个数据集由多个高斯分布混合而成。算法的目标是通过期望最大化(EM)算法估计每个高斯成分的参数(均值、协方差和混合权重),从而对数据进行软聚类。
import numpy as np import matplotlib.pyplot as plt from sklearn.mixture import GaussianMixture from scipy.stats import multivariate_normal from mpl_toolkits.mplot3d import Axes3D # 生成样本数据 np.random.seed(0) n_samples = 1000 mu1, mu2 = (-2, -2, 2), (5, 5, 5) cov1, cov2 = np.eye(3), np.eye(3) * 2 data1 = np.random.multivariate_normal(mu1, cov1, n_samples // 2) data2 = np.random.multivariate_normal(mu2, cov2, n_samples - n_samples // 2) X = np.concatenate((data1, data2), axis=0) # 初始化GMM模型 gmm = GaussianMixture(n_components=2, covariance_type='full') # 训练GMM模型 gmm.fit(X) # 获取模型参数 means = gmm.means_ covariances = gmm.covariances_ weights = gmm.weights_ # 预测每个样本的簇标签 labels = gmm.predict(X) # 可视化结果 fig = plt.figure(figsize=(12, 8)) ax = fig.add_subplot(111, projection='3d') colors = ['navy', 'turquoise'] for i, color in enumerate(colors): x = X[labels == i] ax.scatter(x[:, 0], x[:, 1], x[:, 2], c=color, s=10) # 绘制高斯分布等高面和协方差椭球 u, s, vh = np.linalg.svd(covariances[i]) radii = np.sqrt(s) u = u[:, :2] phi = np.linspace(0, 2 * np.pi, 100) theta = np.linspace(0, np.pi, 100) x_plot = radii[0] * np.outer(np.cos(phi), np.sin(theta)) y_plot = radii[1] * np.outer(np.sin(phi), np.sin(theta)) z_plot = radii[2] * np.outer(np.ones_like(phi), np.cos(theta)) for j in range(x_plot.shape[1]): for k in range(x_plot.shape[0]): [x_plot[k, j], y_plot[k, j], z_plot[k, j]] = np.dot([x_plot[k, j], y_plot[k, j], z_plot[k, j]], vh.T) + means[i] ax.plot_surface(x_plot, y_plot, z_plot, color=color, alpha=0.2) ax.scatter(means[:, 0], means[:, 1], means[:, 2], c='black', s=100, marker='*', label='Means') ax.legend() ax.set_xlabel('Feature 1') ax.set_ylabel('Feature 2') ax.set_zlabel('Feature 3') ax.set_title('GMM Clustering') plt.show()代码首先使用 np.random.multivariate_normal 函数生成了包含两个高斯分布的3维样本数据集,其中一个高斯分布的均值为(-2, -2, -2),协方差矩阵为单位矩阵,另一个高斯分布的均值为(5, 5, 5),协方差矩阵为2倍的单位矩阵。
接下来,我们使用GaussianMixture类初始化了一个GMM模型,指定了要拟合的簇数为2,协方差矩阵类型为’full’。
然后,我们训练GMM模型:调用fit方法对样本数据进行拟合,得到模型参数,包括每个高斯分布的均值、协方差矩阵和权重,调用predict方法预测每个样本所属的簇。
最后,我们可视化结果:创建一个3D图形窗口,并将每个簇的样本数据用散点图表示出来。然后,对于每个高斯分布,使用其均值和协方差矩阵构造协方差椭球,并绘制在图中,以表示高斯分布的形状。最后,将每个高斯分布的均值用星号标记出来,以便于观察。
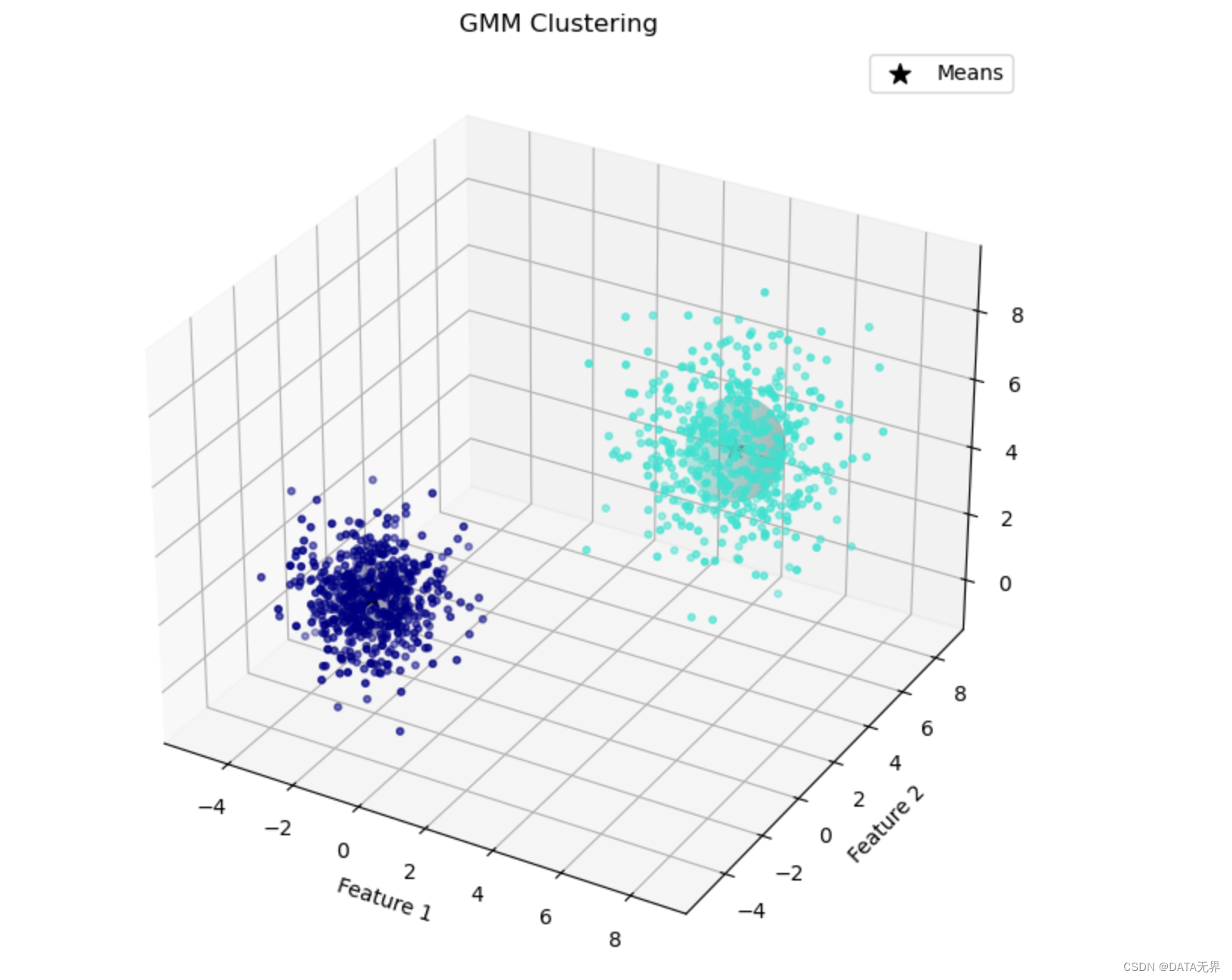
在 Jupyter Notebook 环境中运行上述代码,从输出的3D可视化结果可以看出,GMM算法成功地将数据聚类为两个簇,并较好地捕捉到了每个簇的分布特征。
GMM模型的主要优点是能同时进行聚类和概率密度估计,可以较好地拟合非高斯分布的数据。
但它也存在一些缺陷,例如对离群点敏感、需要预先指定成分数等。通过调整协方差类型、增加稳健性等策略,可以进一步提升GMM的性能。
总的来说,GMM是一种在聚类、异常检测、信号处理等领域都有广泛应用的无监督学习算法。
得益于其能自动从原始数据挖掘隐藏知识的强大能力,无监督学习在诸多行业得到了广泛的应用,包括但不限于:生物信息学、金融、零售、网络安全、推荐系统等。无监督学习还是构建通用人工智能(AGI)的关键技术之一。
随着算力和数据的不断增长,无监督学习无疑将在未来发挥越来越重要的作用,让人工智能系统能像人类一样,从海量原始数据中自主探索和学习,发现更多隐藏的规律和知识。
正是凭借这种"隐形探索者"般的能力,无监督学习将持续为各行业的数据分析和决策注入新的活力,实现AI赋能、释放数据金矿的真正价值。









