GWO简介
灰狼优化算法(Grey Wolf Optimizer,GWO)是一种模仿灰狼狩猎行为的群体智能优化算法,由Seyedali Mirjalili等人在2014年提出。这种算法主要模拟了灰狼的社会等级结构和狩猎策略,用于解决各种优化问题。
在灰狼优化算法中,搜索代理(灰狼)根据Alpha、Beta和Delta的位置来更新自己的位置。这种更新方式反映了狩猎过程中的跟随行为。每个搜索代理的位置更新公式涉及计算与Alpha、Beta和Delta位置的距离,并根据这些距离进行位置调整。
为什么这样进行对比(参考前面几个算法)
- 问题复杂性和算法适应性
- TSP与MTSP的区别:虽然TSP和MTSP都是组合优化问题,但MTSP的复杂度更高,因为它涉及到多个旅行商的同时优化。这种增加的复杂性要求算法具有更好的全局搜索能力和多解处理能力。
- 算法适应性:不同的算法根据其设计原理在不同类型的问题上表现出不同的优势。例如,变邻域搜索(VNS)和大邻域搜索(LNS)在处理单一旅行商的路径优化上可能更为有效,而群体智能算法如GWO可能更适合处理多目标和多解的MTSP。
- 探索与开发平衡
- 探索(Exploration):指的是算法能够探索广阔搜索空间,发现搜索空间中的不同区域。对于MTSP,由于解的空间大大增加,探索能力尤为重要。
- 开发(Exploitation):指算法能够在已发现的有希望区域进行深入搜索,精细调整解。在TSP中,高效的开发能力可以帮助算法快速找到非常接近最优的解。
- 算法性能的全面评估
- 对比不同算法:通过在不同的问题上测试这些算法,可以全面评估它们的性能,包括速度、精度和鲁棒性。比如,VNS可能在TSP中表现优越,但在MTSP中可能需要更多的计算时间或得到较差的结果。
- 实验验证:对比不同算法能够验证理论分析的准确性和实际应用的有效性。这对于科研人员和工程师来说是一个核心环节,帮助他们选择或设计适合具体应用场景的优化工具。
- 提高算法设计和实现的有效性
- 参数调整和算法改进:通过对比分析,研究人员可以发现算法的瓶颈和限制,进而对算法进行参数调整或结构性改进以适应不同的问题。
- 混合算法和创新:对比不同算法的表现也可以激发新的算法设计思路,如结合多种算法的优点来创建混合算法,以提供更优的解决方案。
GWO原理
灰狼是群居动物,其群体结构严格而有序,主要分为四个等级:
1.Alpha:群体的领袖,负责决策和指导群体行动。
2.Beta:处于社会阶层的最低层,经常从事最低等的工作,例如打扫卫生,分发食物。
3.Delta:在Alpha和Beta之下,执行具体任务,如警戒、照顾幼崽等。
4.Omega:位于社会层级最底层,通常承担群体中最低级的工作,如清理、食物分配的最后接受者等。
图1 灰狼群等级制度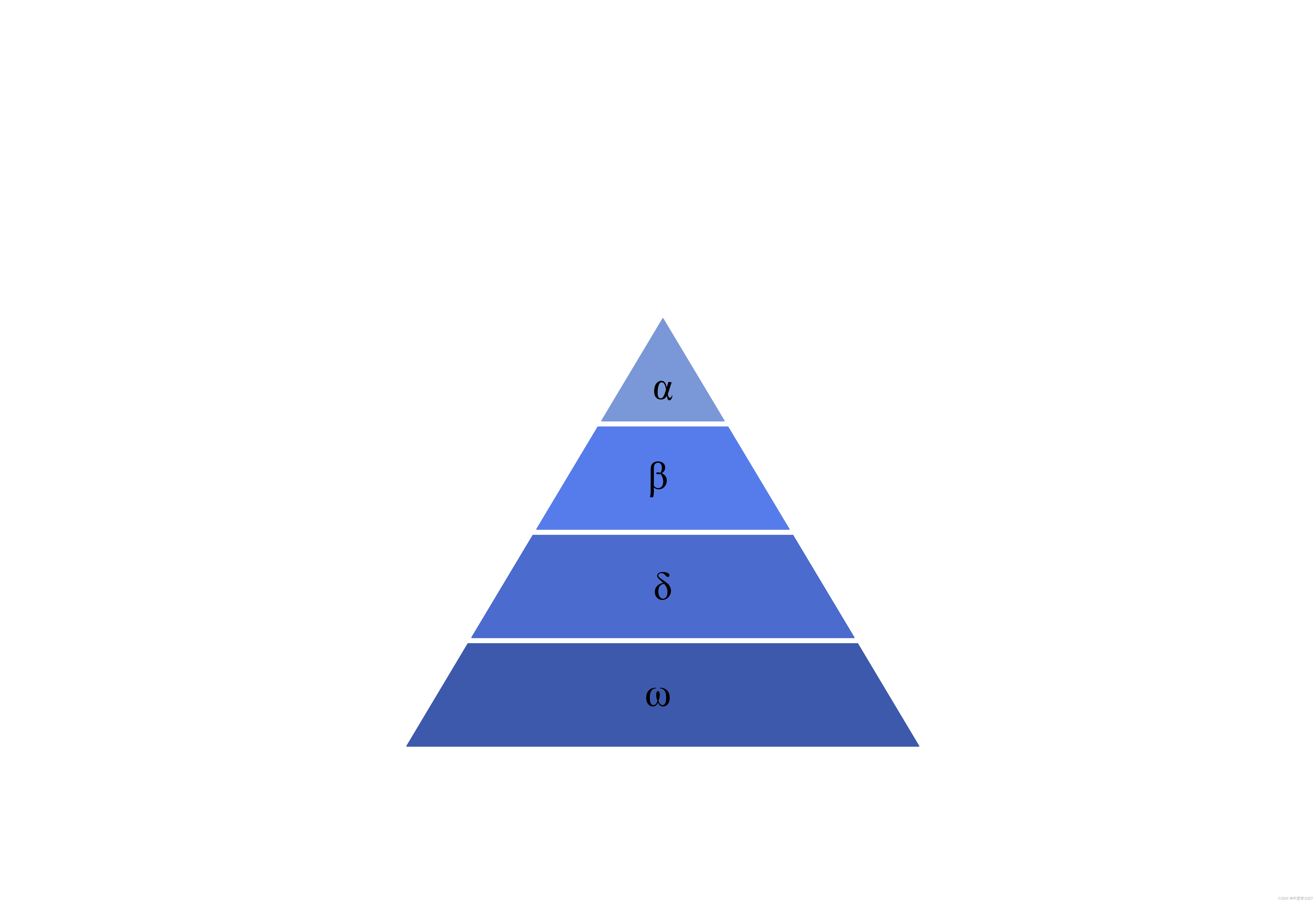
在 GWO 中, 解的搜索代理被视为灰狼群体中的个体, 根据它们的适应度被赋予不同的社会地位, 最优的三个解分别被标记为 α 、 β 、 δ \alpha 、 \beta 、 \delta α、β、δ 。这些领导灰狼引导其他灰狼向更优解区域迁移, 下面详细描述了每个领导角色如何影响位置更新。
(1) α \alpha α
α \alpha α 狼代表当前解空间中的最优解。由于 α \alpha α 地位和对群体的强烈影响力, 其他灰狼倾向于根据 α \alpha α 的位置来调整自己的位置。在维度 k \mathrm{k} k 下, 灰狼 i i i 在 α \alpha α 的引导下的下一个位置更新公式如下:
X α i , k = X α , k ^ − A 1 D α , k ^ X_{\alpha i, k}=X_{\alpha, \hat{k}}-A_1 D_{\alpha, \hat{k}} Xαi,k=Xα,k^−A1Dα,k^
其中, D α , k D_{\alpha, k} Dα,k 计算如下,表示 α \alpha α 与灰狼 i i i 在该维度上的相对距离:
D α , k = ∣ C 1 X α , k − X i , k ∣ D_{\alpha, k}=\left|C_1 X_{\alpha, k}-X_{i, k}\right| Dα,k=∣C1Xα,k−Xi,k∣
而 C 1 C_1 C1 和 A A A ,是调节探索范围和收敛速度的系数,定义如下:
C 1 = 2 r 2 A 1 = 2 a r 1 − a \begin{aligned} & C_1=2 r_2 \\ & A_1=2 a r_1-a \end{aligned} C1=2r2A1=2ar1−a
而 r 1 , r 2 r_1, r_2 r1,r2 是介于 0 和 1 之间的随机数, 它们的主要作用是为算法引入随机性, 这有助于增加解的多样性, 避免算法过早收敛到局部最优解。
(2) β \beta β
β \beta β 狼是第二优解, 它在领导结构中起到辅助 α \alpha α 的作用, 也对群体有一定的引导影响。灰狼 i i i 在 β \beta β 的引导下, 位置更新方式类似,但是依赖于 β \beta β 的位置:
X β i , k = X β , k ˉ − A 2 D β , k X_{\beta i, k}=X_{\beta, \bar{k}}-A_2 D_{\beta, k} Xβi,k=Xβ,kˉ−A2Dβ,k
D β , k D_{\beta, k} Dβ,k 表示的是 β \beta β 与灰狼 i i i 在该维度上的相对距离:
D β , k = ∣ C 2 X β , k ˉ − X i , k ∣ D_{\beta, k}=\left|C_2 X_{\beta, \bar{k}}-X_{i, k}\right| Dβ,k= C2Xβ,kˉ−Xi,k
同 α \alpha α 引导下的更新, C 2 C_2 C2 和 A 2 A_2 A2 定义如下:
C 2 = 2 r 2 A 2 = 2 a r 1 − a \begin{aligned} & C_2=2 r_2 \\ & A_2=2 a r_1-a \end{aligned} C2=2r2A2=2ar1−a
(3) δ \delta δ
δ \delta δ 狼同理,其位置更新式子如下:
X ∂ i , k = X δ , k ^ − A 3 D σ , k X_{\partial i, k}=X_{\delta, \hat{k}}-A_3 D_{\sigma, k} X∂i,k=Xδ,k^−A3Dσ,k
最终, 灰狼 i i i 的位置是 α 、 β 、 δ \alpha 、 \beta 、 \delta α、β、δ 引导下位置的平均值, 这确保了搜索过程从全局最优解中受益,并在搜索过程中逐步精确:
X i , k = X a i , k + X β i , k + X b i , k 3 X_{i, k}=\frac{X_{a i, k}+X_{\beta i, k}+X_{b i, k}}{3} Xi,k=3Xai,k+Xβi,k+Xbi,k
GWO求解方法
编码与解码
编码:假设存在多个城市和若干旅行商,编码阶段通过实数数组进行,每个数组元素代表一个城市,其值指定旅行商编号或城市的访问顺序。
解码:在解码阶段,这些实数值被转换成一个或多个旅行路线,每条路线遵循旅行商访问城市的逻辑顺序,并确保每个城市仅被访问一次,同时使路径尽可能短。
假设有3个旅行商,9个城市,每个旅行商起点为0号城市,其解码图3.7举例如下:
图2 GWO求解MTSP解码图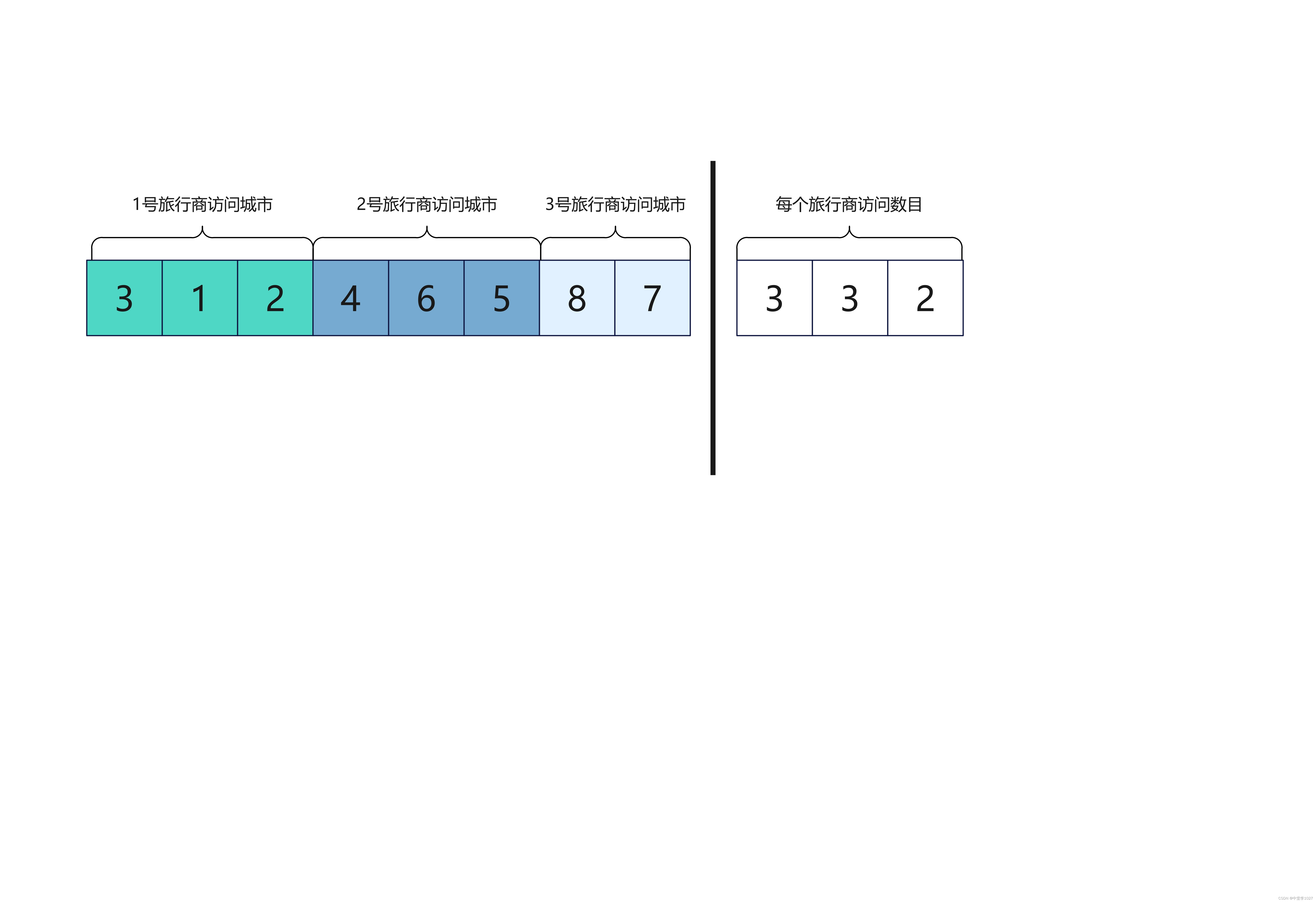
那么,3个旅行商的路线为:
旅行商1:0→3→1→2→0
旅行商2:0→4→6→5→0
旅行商3:0→8→7→0
种群初始化
(1)确定种群大小
选择适当的种群大小极其重要,直接影响搜索广度和算法的计算负担。种群大小需足以探索解空间的不同区域,同时避免过大增加计算复杂度。在本研究中,考虑到城市数量不超过50,设定GWO的种群数目为10000,不会显著影响算法速度。
(2)生成初始解
初始解通常表现为旅行商的行程路径。生成这些解的方法通常包括:
随机生成:通过随机排列城市列表并分割成若干部分,每部分分配给一名旅行商。这种方法虽简单,但可能产生质量较低的解。
启发式方法:应用如最近邻法、最小生成树等基础启发式方法生成更实用的初始解。
然而,本文选择随机生成初始解,因为已频繁使用启发式方法,再次应用意义有限。
(3)考虑约束和目标
初始化时必须考虑MTSP的约束,如每个城市只访问一次,并确保每个旅行商返回起点。此外,应保证初始解分布均匀,避免解空间偏差和局部最优的困境。
(4)参数初始化
除生成初始解外,还需设定算法参数,例如控制参数a。a从较高的初始值(本文设为2)开始,随迭代递减至0,促使算法从广泛探索向精细搜索过渡。
灰狼位置更新
在应用灰狼优化算法(GWO)解决如MTSP的离散优化问题时,传统的连续空间位置更新方法不适用。MTSP的解涉及城市访问顺序,这些是离散变量,而GWO原本设计用于连续变量。因此,要在离散问题如MTSP上实现GWO,需对算法进行修改或引入新策略。本文通过借鉴VNS中的交叉操作方法来更新灰狼位置。位置更新的流程如图所示:
图3 GWO位置更新流程图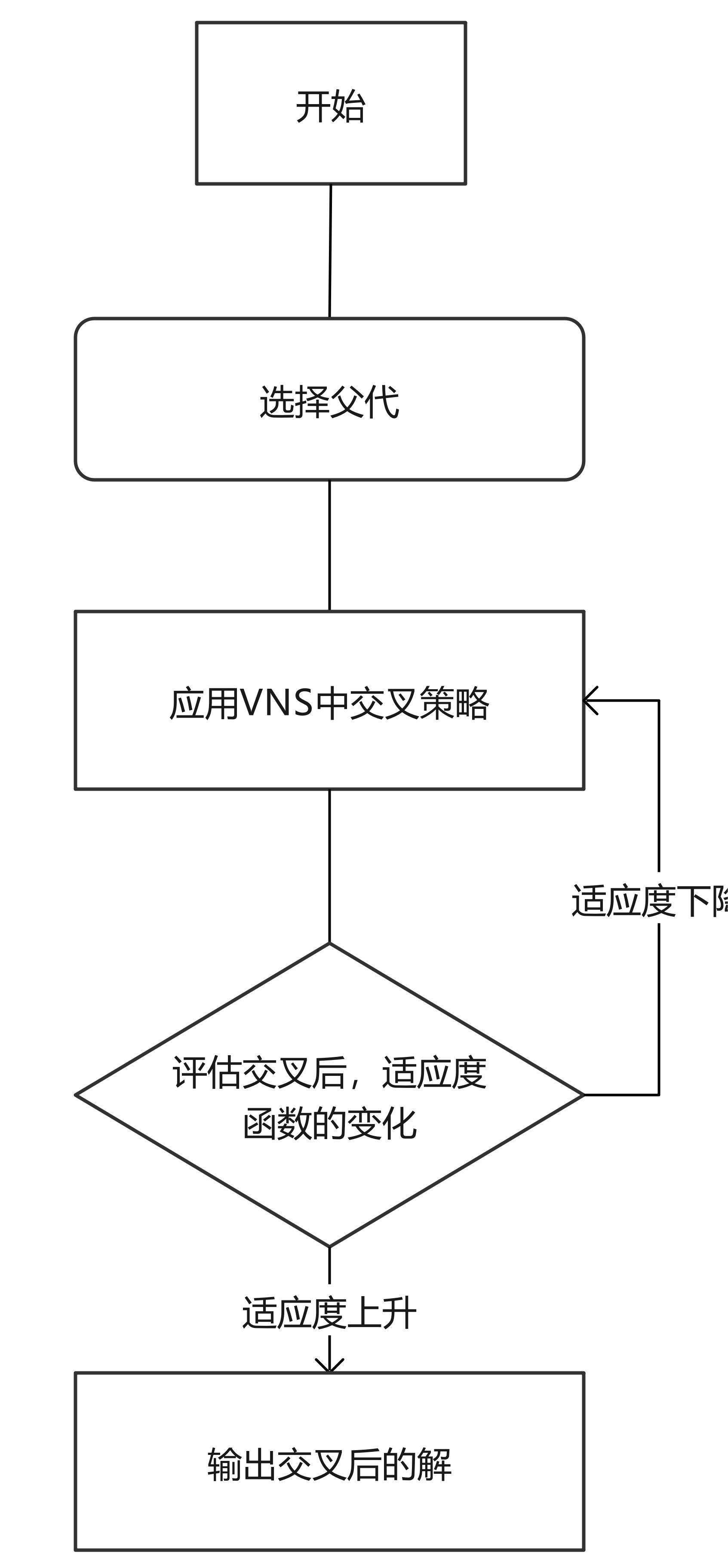
局部搜索操作
局部搜索的介绍可能显得抽象,因此本文通过具体案例来阐述整个过程::
以一个涉及4名旅行商和20个城市的MTSP为例,所有旅行商从同一个起点城市(城市0)出发并返回此地。初始路径配置如下:
旅行商1:0→1→2→3→0
旅行商2:0→4→5→6→7→0
旅行商3:0→8→9→10→11→12→0
旅行商4:0→13→14→15→16→17→18→19→0
首先,随机确定要破坏的路线数量 k k k,设 k = 2 k=2 k=2。这意味着随机选择两条路线进行破坏和后续的重构。
对每条选定的路线, 计算可以从中移除的最大城市数 L max L_{\text {max }} Lmax 。例如, 如果选中了旅行商 1 和旅行商 3 , 根据当前解中每条路径上城市数目的平均值 t 1 t_1 t1 和当前路径城市数目的较小者计算 L max L_{\max } Lmax :
平均城市数 : t ˉ 1 = 3 + 4 + 5 + 8 4 = 5 旅行商 1 : L max = min ( 5 , 3 ) = 3 旅行商 3 : L max = min ( 5 , 5 ) = 5 \begin{aligned} &平均城市数: \bar{t}_1=\frac{3+4+5+8}{4}=5 \\ &旅行商1: L_{\max }=\min (5,3)=3 \\ &旅行商3: L_{\max }=\min (5,5)=5 \end{aligned} 平均城市数:tˉ1=43+4+5+8=5旅行商1:Lmax=min(5,3)=3旅行商3:Lmax=min(5,5)=5
根据计算出的 L max L_{\max } Lmax, 从每条路径上随机移除 l l l 个城市:
从旅行商 1 的路径随机移除 2 个城市
从旅行商 3 的路径随机移除 4 个城市。
破坏后, 通过启发式方法, 如最近邻法或插入法, 重新安排被移除的城市, 这包括将城市重新插入原有或新的路径中。重构的主要目标是减少总旅行距离, 同时确保每个旅行商的路线保持可行。
新解经评估函数 (本文中为总旅行距离) 验证后需与当前解比较。如新解减少了旅行距离或改善了性能, 则被接受; 否则, 可能需重新破坏或保留原解。
破坏和重构的局部搜索策略为复杂路由优化问题提供了有效解决方案。通过有目的的破坏和智能重构, 可以显著提高算法的解空间探索能力, 从而找到更优的解决方案。
GWO算法流程图
图4 GWO求解MTSP解码图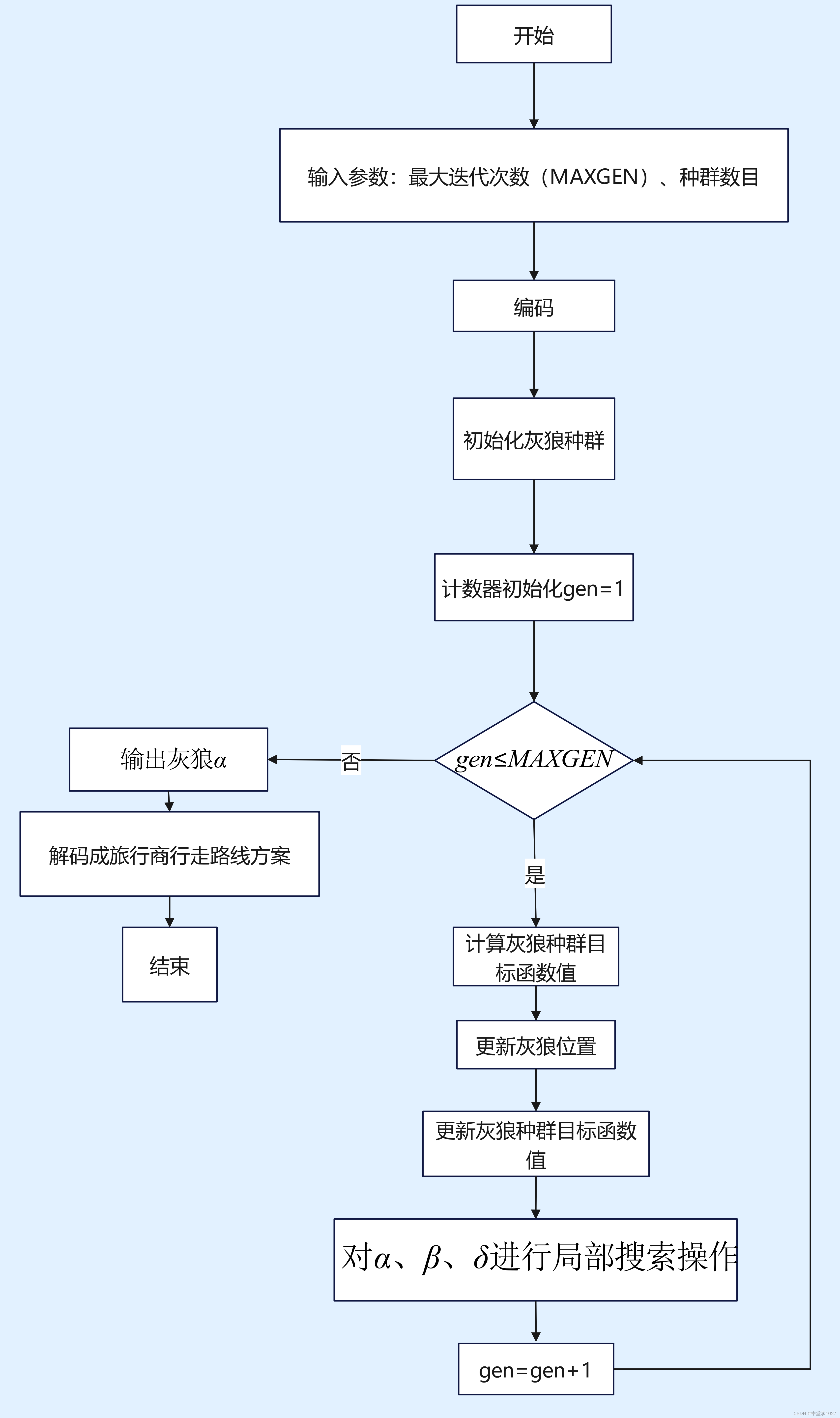
种群初始化
function population=init_pop(NIND,n,m,start) %% 初始化灰狼种群 %输入NIND: 种群数目 %输入n: 城市数目 %输入m: 旅行商数目 %输入start: 起(终)点城市 %输出population: 灰狼种群 len=n+m-1;%个体长度 %这个个体长度为什么是n+m-1,n为城市数目,m-1为分隔符,一般用正负数来区别,你也可以自己设置特殊的分隔符 %例如假设第一个旅行商访问城市1,2,3,第二个旅行商访问城市4和5。我们可以用特殊的分隔符, %比如0或者一个负数,来区分两个旅行商的路线。一个可能的编码如下: %1,2,3,-1,4,5那么-1就是分隔符 population=zeros(NIND,len);%初始化种群 for i=1:NIND population(i,:)=encode(n,m,start); end end解码与编码
function individual=encode(n,m,start) %输入n: 城市数目 %输入m: 旅行商数目 %输入start: 起(终)点城市 %编码 %输出individual: 灰狼个体 part1=randperm(n); part1(part1==start)=[];%删除起点 part2=zeros(1,m);%初始化每个旅行商访问城市数目 if m == 1 part2=n-1; else for i = 1:m if i == 1 right=n-1-(m-1);%最大取值,n-1代表除起点的城市数目,m-1代表除最后一个城市之外的其他旅行商,-1其实就是减去自身 %例如6个城市,3个旅行商,第一个旅行商最多走3个(除开起点) part2(i)=randi([1,right],1,1); elseif i == m part2(i)=n-1-sum(part2(1:(i-1)));%意味着到了最后一个旅行商直接减去之前的旅行商访问城市的数目 else right=n-1-(m-i)-sum(part2(1:(i-1))); part2(i)=randi([1,right],1,1); end end end individual=[part1,part2]; endfunction RP=decode(individual,n,m,start) % RP=cell(m,1);%初始化m条行走路线 part1=individual(1:n-1);%提取城市排序序列 part2=individual(n:end);%提取各个旅行商访问城市数目 for i = 1:m if i == 1 left=1;%起点序号 right=part2(i); route=[start,part1(left:right),start]; else left=sum(part2(1:(i-1)))+1;%起点就是前面旅行商一共走了多少城市数目,然后加一。 right=sum(part2(1:i)); route=[start,part1(left:right),start]; end RP{i,1}=route; end end目标函数值计算
适应度函数用于评判位置更新后调整效果
function obj=obj_function(population,n,m,start,dist) %输出population: 灰狼种群 %输入n: 城市数目 %输入m: 旅行商数目 %输入start: 起(终)点城市 %输入dist: 距离矩阵 %输出obj: 灰狼种群的目标函数值 NIND=size(population,1);%种群数目,例如population有6行就代表有6种方案 obj=zeros(NIND,1);%初始化种群目标函数值 for i = 1:NIND individual=population(i,:);%第i个灰狼个体 RP=decode(individual,n,m,start);%解码 [~,~,maxETD]=travel_distance(RP,dist); obj(i)=maxETD; end end计算行走距离与路线距离
function [sumTD,everyTD,maxETD]=travel_distance(RP,dist) %输入RP: 旅行商行走路线方案 %输入dist: 距离矩阵 %输出sumTD: 所有旅行商的行走总距离 %输出everyTD: 每个旅行商的行走距离 %输出maxETD: everyTD中的最大值 m=size(RP,1); %旅行商数目 everyTD=zeros(m,1); %初始化每个旅行商的行走距离 for i=1:m route=RP{i}; %每个旅行商的行走路线 everyTD(i)=route_length(route,dist); end sumTD=sum(everyTD); %所有旅行商的行走总距离 maxETD=max(everyTD); %everyTD中的最大值 endfunction len=route_length(route,dist) n=numel(route); %这条路线所经过城市的数目,包含起点和终点城市 len=0; for k=1:n-1 i=route(k); j=route(k+1); len=len+dist(i,j); end end交叉函数
灰狼优化算法(GWO)结合交叉操作处理MTSP的原因
在灰狼优化算法(GWO)中处理多旅行商问题(MTSP)时,采用类似遗传算法中的交叉操作主要是为了应对GWO位置更新函数的连续性特征与MTSP的离散性特点之间的不匹配。GWO的位置更新机制原本设计用于连续优化问题,需要适当修改以适应离散问题如MTSP。以下是如何结合这两种思想,并解释为什么这种方法是有益的:
- GWO的位置更新公式
在GWO中,个体的位置更新受到领导者(α, β, δ)的引导。这些领导者的位置反映了当前解空间中的最优解。通过模拟这些领导者的位置,其他个体调整自己的位置以探索新的可能解。位置更新公式涉及到计算与领导者的相对距离并根据这些距离调整位置。这种方法在连续空间中是非常有效的,因为它支持平滑的过渡和连续的探索。
- MTSP的离散特性
然而,MTSP是一个离散问题,每个解都是一个城市访问序列。在这样的序列中,简单的“距离”概念不再适用,而是需要考虑城市之间的交换、插入或逆转等操作来调整序列。
- 结合交叉操作的优势
- 保持解的合法性:传统的GWO更新可能会生成不符合MTSP约束的解,例如城市重复访问。通过采用遗传算法的交叉操作,可以确保生成的子代保持解的合法性,即每个城市恰好访问一次。
- 引入离散搜索动态:遗传算法的交叉操作特别适合处理离散变量,可以通过重组两个有效解的部分来探索新的解空间,同时保持一些从父代继承的优良特质。
- 提高搜索多样性和全局探索能力:GWO的探索能力通过领导者的引导实现,结合交叉操作可以进一步增强搜索的多样性和全局探索能力,特别是在复杂的解空间中。
- 平衡探索与开发:通过结合GWO的全局引导和遗传算法的局部操作(如交叉和突变),可以更好地平衡解的探索与开发,提高算法的总体性能。
- 实现方法
- 将灰狼群体中最优的几个个体(α, β, δ)视为“父代”。
- 对这些领导者的序列进行交叉操作,生成新的个体序列。
- 采用遗传算法中的交叉策略(如部分映射交叉PMX,顺序交叉OX等),以确保子代的合法性和多样性。
当考虑将灰狼优化算法(GWO)适应多旅行商问题(MTSP)等离散优化问题时,除了采用遗传算法中的交叉操作外,还可以通过其他几种方法来处理算法的离散化和适配问题。也可采用以下方法:
-
使用序列操作
除了交叉,还可以使用其他特定于序列的操作来适应GWO的位置更新。这些操作包括:
- 插入操作:随机选择一个元素(城市)并将其插入到序列中的另一个位置。
- 逆转操作:随机选择序列中的一段并将其逆序排列。
- 交换操作:随机选择序列中的两个元素并交换它们的位置。
这些操作可以在模拟灰狼的位置更新时使用,以保持解的离散性质和问题约束的符合性
-
映射连续到离散
将GWO中的连续位置更新映射到离散解空间中。这可以通过以下方式实现:
-
离散映射:将连续空间中的位置映射到最近的整数或使用特定的规则选择序列中的位置。例如,可以根据连续值的相对大小来决定城市在序列中的位置。
-
排名映射
排名映射是一种将连续值转换为离散序列的方法。具体操作如下:
- 将每个连续值关联到一个特定的城市。
- 根据连续值的大小对这些城市进行排序,生成一个城市访问序列。
- 这种方法可以直接应用于生成TSP或MTSP的解,其中连续值的大小直接决定城市访问的顺序。
-
优先级编码
在优先级编码中,每个连续变量的值被解释为该变量(或城市)的优先级。解的构造如下:
- 根据每个连续值的大小确定每个城市的访问优先级。
- 高优先级的城市在生成的路径中位置较前。
- 这种方法特别适用于需要考虑优先级或偏好的情景,例如有时间窗或特定访问顺序的要求。
-
竞赛选择(Tournament Selection)
竞赛选择常见于遗传算法,但也可以用于将连续值映射到离散解:
-
设定一个“竞赛”大小,比如每次从连续值列表中随机选择几个元素。
-
选取这些元素中的最大值(或最小值),将其映射到一个离散的选择上。
-
这可以用于决定哪个城市下一个被访问,依此类推,直到构建完整的路线。
-
概率比例选择
这种方法将连续值转换为选择概率:
- 将连续值转换为概率分布,例如通过规范化确保所有值的总和为1。
- 使用这些概率来随机选择下一个访问的城市,高概率值意味着更大的选择机会。
- 这种方法允许解决方案在探索和开发之间保持动态平衡,可能在每次迭代中产生不同的路线。
-
热编码映射
热编码通常用于将分类数据转换为机器学习模型可用的格式,也可以用于离散映射:
- 将连续值区间分割成多个桶,每个桶代表一个城市。
- 连续值落在哪个桶中,就选择对应的城市。
- 通过这种方式,连续值被编码为一系列的0和1,其中1表示选中的城市。
function [individual1,individual2]=cross(individual1,individual2,n) cities_ind1=individual1(1:n-1);%灰狼个体1的城市序列 cities_ind2=individual2(1:n-1);%灰狼个体2的城市序列 L=n-1;%灰狼个体的城市序列数目 while 1 r1=randsrc(1,1,[1:L]); r2=randsrc(1,1,[1:L]); if r1~=r2 s=min([r1,r2]); e=max([r1,r2]); a0=[cities_ind2(s:e),cities_ind1]; b0=[cities_ind1(s:e),cities_ind2]; for i = 1:length(a0) aindex=find(a0==a0(i)); bindex=find(b0==b0(i)); if length(aindex)>1 a0(aindex(2))=[]; end if length(bindex)>1 b0(bindex(2))=[]; end if i == length(cities_ind1) break end end cities_ind1=a0; cities_ind2=b0; break end end individual1(1:n-1) = cities_ind1; % 更新灰狼个体1的中城市序列 individual2(1:n-1) = cities_ind2; % 更新灰狼个体2的中城市序列 end局部搜索函数
局部搜索在GWO中的应用可以帮助算法在找到潜在优良区域后,更细致地探索这些区域,从而找到更优的局部解。
一般步骤如下:
- 选择局部搜索策略:根据问题的性质选择合适的局部搜索方法,如2-opt、3-opt等(对于路径问题),或者更简单的基于邻域的搜索策略。
- 触发条件:确定何时执行局部搜索。一些常见的触发条件包括:
- 在每次迭代后执行局部搜索。
- 当算法进展缓慢或停滞时执行。
- 仅对表现最好的几个解执行局部搜索。
- 执行局部搜索:一旦触发局部搜索,选定的搜索方法将应用于当前解或群体中的一部分。这通常涉及到对解的小范围修改,以探索解的近邻。
- 更新解:如果局部搜索找到了更好的解,则更新当前解或群体中相应的解。
function [individual,ind_obj]=LocalSearch(individual,n,m,k,start,dist) alpha_RP=decode(individual,n,m,start); %将灰狼个体解码为旅行商行走方案 [~,~,alpha_TD1]=travel_distance(alpha_RP,dist); %灰狼个体的目标函数值 [removed1,sdestroy1]=remove(alpha_RP,n,m,k,start,dist); %对灰狼个体进行移除操作 s_alpha=repair(removed1,sdestroy1,dist); %对灰狼个体进行修复操作 [~,~,alpha_TD2]=travel_distance(s_alpha,dist); %灰狼个体修复后的目标函数值 if alpha_TD2j};%当前路径 [~,deltaC]=insRoute(visit,route,dist,maxETD);%插入遗憾值最小的城市 dec=[dec;deltaC]; ins=[ins;j]; end [sd,sdi]=sort(dec);%升序排列dec insc=ins(sdi); %将ins的序号与dec排序后的序号对应 ri(i)=insc(1);%更新当前城市最好插回路径 if size(dec,1)1 de12=sd(2)-sd(1); rid(i)=de12; else de12=sd(1); rid(i)=de12; end end %根据rid rid最大的城市就是先插回的城市 [~,firIns]=max(rid); %找出遗憾值最大的城市序号 rIns=ri(firIns); %插回路径序号 %将firIns插回到rIns srepair{rIns,1}=insRoute(removed(firIns),srepair{rIns,1},dist,maxETD); %将removed(firIns)城市从removed中移除 removed(firIns)=[]; endfunction sdestory=dealRemove(removed,RP) %输入removed: 被移出的城市集合 %输入RP: 旅行商行走路线方案 %输出sdestroy: 移出removed中的城市后的RP sdestory=RP; nre=length(removed); m=size(RP,1); for i = 1:m route=RP{i}; for j = 1:nre findri=find(route==removed(j),1,"first"); if ~isempty(findri) route(route==removed(j))=[]; end end sdestory{i}=route; end sdestory=deal_rp(sdestory); end插入成本
插入成本类似于LNS里的遗憾值
function [newRoute,deltaC]=insRoute(visit,route,dist,maxETD) %输入visit 待插入城市 %输入route: 一条行走路线 %输入dist: 距离矩阵 %输出newRoute: 将visit插入到当前路线最佳位置后的行走路线 %输出deltaC: 将visit插入到当前路线最佳位置后的插入成本 start=route(1); rcopy=route;%复制路线 %%先将城市插回到增量最小的位置 rcopy(rcopy==start)=[];%将start从rcopy中删除 lr=numel(route)-2;%除去起点城市和终点城市外,当前路径上的城市数目 rc0=[];%记录插入城市后符合约束的路径 delta0=[];%记录插入城市后的增量 for i = 1:lr+1 if i==lr+1 rc=[start,rcopy,visit,start]; elseif i==1 rc=[start,visit,rcopy,start]; else rc=[start,rcopy(1:i-1),visit,rcopy(i:end),start]; end %这里插入的位置可以自由切换,因为从设计的角度来说,放哪其实都可以,反正后面有遗憾值为这个设计兜底 rc0=[rc0;rc]; alen=route_length(rc,dist); dif=alen-maxETD;%计算插入成本,这里与LNS的遗憾值类似 delta0=[delta0;dif];%将插入成本存储到delta0 end [deltaC,ind]=min(delta0); newRoute=rc0(ind,:); end切换行走方案与灰狼个体(确认元胞数组里的路径)
function individual=change(RP) %% 行走方案与灰狼个体之间进行转换 %输入RP: 旅行商行走路线方案 %输出individual: 灰狼个体 m=size(RP,1); %旅行商数目 individual=[]; lr=zeros(1,m); %每个旅行商所服务的城市数目 for i=1:m route=RP{i}; start=route(1); route(route==start)=[]; lr(i)=numel(route); individual=[individual,route]; end individual=[individual,lr]; end绘图函数
function draw_Best(RP,vertexs,start) %% 画出旅行商行走路线方案路线图 %输入RP: 旅行商行走路线方案 %输入vertexs: 各个城市的横纵坐标 %输入start: 起(终)点城市 start_v=vertexs(start,:); %起点城市坐标 m=size(RP,1); %旅行商数目 figure hold on;box on title('最优行走方案路线图') hold on; C=hsv(m); for i=1:size(vertexs,1) text(vertexs(i,1)+0.5,vertexs(i,2),num2str(i)); end for i=1:m route=RP{i}; %第i个旅行商的行走路线 len=numel(route); %第i个旅行商所访问的城市数目(包括起点和终点城市) fprintf('%s','旅行商',num2str(i),':'); for j=1:len-1 fprintf('%d->',route(j)); c_pre=vertexs(route(j),:); c_lastone=vertexs(route(j+1),:); plot([c_pre(1),c_lastone(1)],[c_pre(2),c_lastone(2)],'-','color',C(i,:),'linewidth',1); end fprintf('%d',route(end)); fprintf('\n'); end plot(vertexs(:,1),vertexs(:,2),'ro','linewidth',1);hold on; plot(start_v(1,1),start_v(1,2),'s','linewidth',2,'MarkerEdgeColor','b',... 'MarkerFaceColor','b','MarkerSize',10); end主函数
clc clear close all tic data=load('input.txt'); x=data(:,2); y=data(:,3); vertexs=data(:,2:3); n=size(data,1); h=pdist(vertexs); dist=squareform(h); %%参数设置 m=2;%旅行商数目 start=1;%起点参数 NIND=50;%种群数目 MAXGEN=1000;%最大迭代次数 k=m;%移除相邻城市数目 %%初始化种群 population=init_pop(NIND,n,m,start); init_obj=obj_function(population,n,m,start,dist); %%开始优化 gen=1; best_alpha=zeros(MAXGEN,n+m-1);%记录每次迭代过程中全局最优灰狼个体 best_obj=zeros(MAXGEN,1);%记录每次迭代过程中全局最优灰狼个体的目标函数值 alpha_individual=population(1,:); %初始灰狼α个体 alpha_obj=init_obj(1); %初始灰狼α的目标函数值 beta_individual=population(2,:); %初始灰狼β个体 beta_obj=init_obj(2); %初始灰狼β的目标函数值 delta_individual=population(3,:); %初始灰狼δ个体 delta_obj=init_obj(3); %初始灰狼δ的目标函数值 while genbeta_obj && obj(i,1)
-
-
-
- 实现方法
- 结合交叉操作的优势
- MTSP的离散特性
- GWO的位置更新公式









