毕业设计-基于协同过滤算法的个性化推荐系统

目录

前言

课题背景和意义

实现技术思路

一、预备知识

二、基于SlopeOne的协同过滤推荐优化算法

三、基于改进 Ｋ⁃ｍｅａｎｓ 的协同过滤推荐优化算法

四、结论及展望

实现效果图样例

最后

前言

    📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。

🚀对毕设有任何疑问都可以问学长哦!

选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277

大家好,这里是海浪学长毕设专题,本次分享的课题是

🎯毕业设计-基于协同过滤算法的个性化推荐系统

课题背景和意义

大数据时代下互联网的应用使人们的生活更 加便捷与智能化。 但随之而来的“信息过载”问题 亟需解决，此时推荐系统应运而生。 协同过滤作为个性化推荐系统中应用较为广泛的一种算 法，因经常面临数据稀疏性和算法扩展性问题，近 年来备受关注。 因此，协同过滤算法的优化成为了 国内外学者的研究热点。 针对数据稀疏性问题，一些学者通过降维的方法来缓解稀疏性，提出了基于矩阵分解的迭代最小二乘加权正 则化协同过滤算法，对传统矩阵分解模型加入正则 化约束以防止过拟合； 还 有一些学者通过矩阵填充来缓解数据稀疏性. 针对算法扩展性问题，采用了Ｋ⁃ｍｅａｎｓ 聚类、二分 Ｋ⁃ｍｅａｎｓ 聚类、模糊 Ｋ⁃ｍｅａｎｓ聚类先对物品进行聚类再推荐的方法，进 而提高了推荐的精度和可扩展性；上述方法推荐精度均得到显著提高，数据稀疏性和扩展性问题得到了有效改善。 本文研究结论不仅可进一 步丰富协同过滤推荐算法的现有理论成果，还可以为提高推荐系统的精度提供理论依据和决策参考。

实现技术思路

一、预备知识

SlopeOne算法

SlopeOne算法基本原理是计算不同物品间的一个评 分差，用评分差预测最终用户对物品的评分。 若将 整个评分数据标记为 Ｒ，主要分以下两步：

①在两个物品同时被评分的前提下，将两物品 i、j的评分差取均值，记做评分偏差：

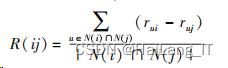
 其中，ｒｕｉ和 ｒｕｊ表示用户 ｕ 对项目 ｉ、ｊ 的评分， Ｎ（ｉ）是对物品 ｉ 评过分的用户， ｜ Ｎ（ ｉ）∩Ｎ（ ｊ） ｜ 是 对物品 ｉ、ｊ 都评过分的用户数。

②根据用户历史评分和由上式子得出的评分偏 差，预测用户对没有做出过评分的物品的分值。

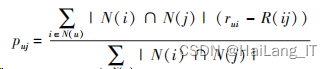
基于 Ｋ⁃ｍｅａｎｓ 聚类的协同过滤推荐算法

设 Ｘ ＝ ｛ｘｉ ｜ ｘｉ∈Ｒ ｐ ，ｉ ＝ １，２，…，ｎ｝为原数据集， 每个数据由用户、项目、评分 ３ 部分组成。 设目标 用户 为 ｕ， 用 户 集 合 是 Ｕ ＝ ｛ ｕ１ ， ｕ２ ， …， ｕｍ ｝， Ｋ⁃ｍｅａｎｓ聚类得出的用户集合可以表示为 Ｕ ＝ ｛Ｃ１ ， Ｃ２ ，…，Ｃｋ｝，ｋ 为聚类个数。 算法步骤如下：

（１） 在 Ｘ 中随机选出个样本作为初始簇心 Ｍｉ（ｉ ＝ １，２，…，ｋ）；

（２）用初始簇心 Ｍｉ （ ｉ ＝ １，２，…，ｋ） 对用户⁃项 目评分矩阵 Ｒｍ × ｎ 执行经典 Ｋ⁃ｍｅａｎｓ 算法，得到 ｋ 个类；

（３）使用欧氏距离计算目标用户 ｕ 与 ｋ 个簇 心间的距离，根据最小距离，找到 ｕ 所属的类别；

（４）在 ｕ 所属类中，计算 ｕ 与其他用户的相似 性，获取 ｕ 的最近邻居集 Ｎｕｊ（ｊ ＝ １，２，…，ｍ）；

（５）得到最近邻居集后，预测求得想要推荐给 ｕ 的项目的评分，由高到低排序后，把前 Ｎ 个项目 推荐给 ｕ。

二、基于SlopeOne的协同过滤推荐优化算法

为有效缓解数据稀疏性， 选取 ＭｏｖｉｅＬｅｎｓ １００ｋ 数据集，数据集详情如表。

 （实验环境为 Ｗｉｎｄｏｗｓ ８ 系统；硬件条件为 ＣＰＵ２． ３ＧＨＺ，４Ｇ 内存，１００Ｇ；使用软件 Ｐｙｔｈｏｎ ３． ７ 版本）我们选取 ９ 种不同方法进行稀疏矩阵的填 充，并选用均方根误差（ＲＭＳＥ）来判定有效性。用全局均值法、用户平均 法、物品平均法、用户活跃度 ＆ 物品不平均、用户 活跃度 ＆ 物品平均、用户不平均 ＆ 物品流行度、用 户平均 ＆ 物品流行度、用户活跃度 ＆ 物品流行度、SlopeOne这 ９ 种不同方法进行填充，其均方根误 差见表：

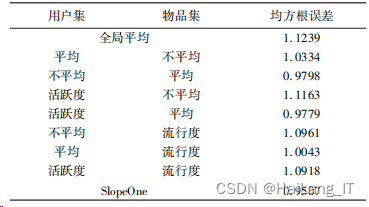
从上表的结果可以看出，当使用SlopeOne方法 进行填充时，其 ＲＭＳＥ 是最小的，说明使用该方法填 充时误差较小。 下面我们将采用SlopeOne方法对 ＭｏｖｉｅＬｅｎｓ １００ｋ 版本数据集进行填充，结果见表。 

 由表可知，进行了矩阵填充后，数据集的稀 疏度变为 ６.37％ ，说明运用SlopeOne 填充的效果明显。 使用填充后数据设计了两组对比实验， 以验证有效性：

实验 １

确定最佳聚类个数。 在这一阶段的 实验中，分别利用由 Ｓｌｏｐｅ Ｏｎｅ 填充前和填充后的 数据，得到两个最佳 Ｋ⁃ｍｅａｎｓ 聚类个数。 在确定过 程中，我们选取平均绝对误差（ＭＡＥ） 作为测量标 准，当聚类个数以 ２ 为间隔，由 ２ 增加到 ２０ 时，根 据 ＭＡＥ 的大小来确定出最佳聚类个数，为了保证 推荐时选取的近邻数相同，将其固定为 ２５，以此增 强 ＭＡＥ 值的可靠性。 图中纵坐标代表 ＭＡＥ 值， 横坐标是聚类个数。

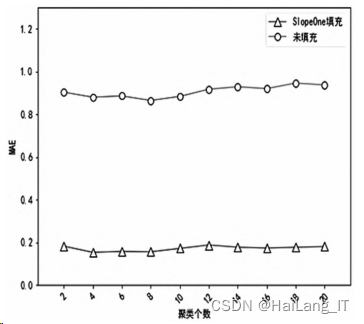
实验结果表明：图中随着聚类个数从 ２ 增加 到 ２０，在进行 ＳｌｏｐｅＯｎｅ 填充和未填充时，Ｋ⁃ｍｅａｎｓ不同聚类个数的 ＭＡＥ 值都呈现出先下降后上升的 趋势，且波动幅度较小。 两种情况的 ＭＡＥ 最低值 都出现在 ｋ ＝ ８，因此最佳的聚类个数都是 ８。

实验 ２

推荐算法精度对比。 我们采用三种 算法来做对比试验，分别是：基于 ＳｌｏｐｅＯｎｅ 填充后 的 Ｋ⁃ｍｅａｎｓ 协同过滤推荐、经典 Ｋ⁃ｍｅａｎｓ 协同过滤 推荐和传统的协同过滤推荐算法。 图中纵轴是 ＭＡＥ 值，横轴是近邻个数，以 ５ 为间隔从 ５ 增加到 ５０，结果如图所示。

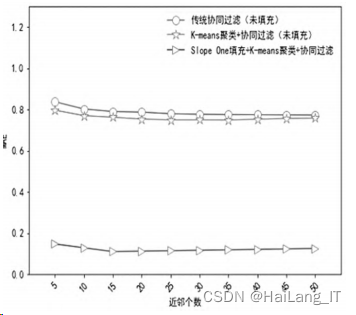
 由图可以看出，三种协同过滤推荐算法的 ＭＡＥ 值都随着最近邻个数的增加呈现出缓慢下降 的趋势，且在邻居个数变化相同时，用 Ｓｌｏｐｅ Ｏｎｅ 填 充后的 Ｋ⁃ｍｅａｎｓ 聚类协同过滤算法的 ＭＡＥ 值最 小。 因此，在推荐之前，先对评分矩阵进行填充，这 样能增加一些用户评分数据，以便在推荐过程中发 掘出更多的可供推荐的项目，填充完毕的矩阵再对用户进行 Ｋ⁃ｍｅａｎｓ 聚类，这样是为了能缩小近邻寻 找范围，类中的所有用户相比类外的用户与目标用 户具有更高的相似程度，在后续的近邻匹配选取时 也就更便利。

三、基于改进 Ｋ⁃ｍｅａｎｓ 的协同过滤推荐优化算法

基于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 算法

由于第 ２ 节中用到的传统 Ｋ⁃ｍｅａｎｓ 聚类算法 的初始中心和聚类个数 ｋ 均是随机产生的，其合理 性会影响聚类结果。首先给出如下定义：

任意两个数据点间距离的平均值为：

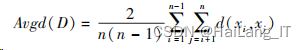
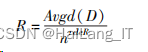
ｒｅｌｅＲ 是一个用来调节的系数， ｒｅｌｅＲ 取 ０． １３ 时，聚类效果最好。

定义 ３ 点的聚集度定义：

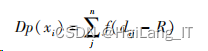
 定义 ４ 簇类平均距离定义为：

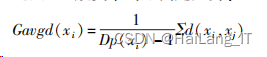
 簇类平均距离 Ｇａｖｇｄ（ ｘｉ ） 衡量的是元素密集 度，数值越小，说明在目标用户 ｘｉ 所在类中，数据 点之间越紧凑。

定义 ５ 聚集度距离 Ｇ（ｘｉ）定义为：

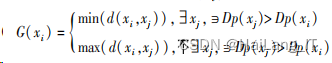
 Ｇ（ｘｉ）是通过比较聚集度 Ｄｐ（ｘｉ）来确定的，用它 来衡量不同簇之间的差异性。 在所有的点中，当 ｘｉ 的 聚集度最大时，Ｇ（ｘｉ）是 ｘｉ 与剩余所有点之间的最大 距离，反之则为 ｘｉ 与剩余所有点之间的最小距离。

定义 ６ 中心聚集参数定义为：

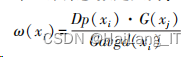
 基于以上概念，我们给出基于中心聚集参数的 改进 Ｋ⁃ｍｅａｎｓ 算法流程： 输入：所有的数据集点 ｘ１ ，ｘ２ ，…，ｘｎ 输出：聚类结果

（１）计算出每个点的中心聚集参数 ω（ｘｉ）；

（２）选出使得 ω（ ｘｉ）最大的点 ｘｉ，由它做为第 一个初始聚类中心，计算出 ｘｉ 与剩余点间的距离， 将得到的距离值与邻域半径 Ｒ 作比较，若距离小 于 Ｒ 则说明可以与 ｘｉ 划为一类，因此将从数据点 中除去这些点，若距离大于 Ｒ，则说明与 ｘｉ 的距离 过远，不适宜与 ｘｉ 归为一类，因此将这些点保留下 来，进行下一步；

（３）在第（２）步中保留下的点里再选出 ω（ｘｉ）最 大的点，作为第 ２ 个聚类中心，再次操作步骤（２）；

（４） 一直重复操作步骤（３），当数据集中的点 ｘ１ ，ｘ２ ，…，ｘｎ 全部去除为止；

（５）输出 ｋ 个最优初始中心 Ｍｉ（ｉ ＝１，２，…，ｋ）；

（６） 利用初始簇心 Ｍｉ，对 Ｒｍ × ｎ 执行 Ｋ⁃ｍｅａｎｓ 算法，将数据集分成 ｋ 类；循环执行 Ｋ⁃ｍｅａｎｓ 算法， 直至其准则函数收敛，得到最终聚类结果；

为验证上述算法的有效性，我们选取以下 ＵＣＩ 数据集进行验证，同时选取的评价标准 有：调整后的兰德指数 （ ＲＩ）、 互信息 （ ＭＩ） 以及 Ｆｏｗｌｋｅｓ⁃Ｍａｌｌｏｗｓ 指标。

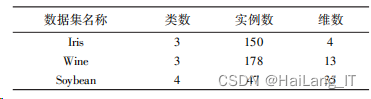
调整兰德指数指标对比

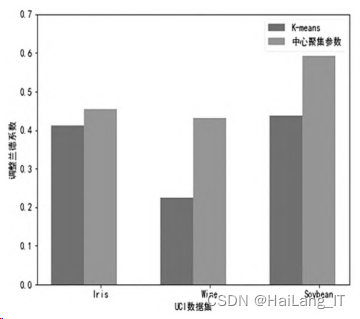
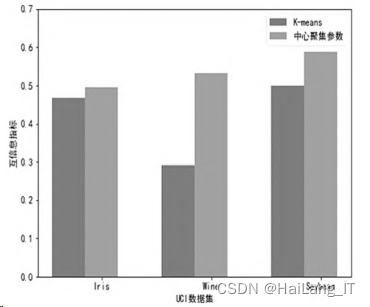
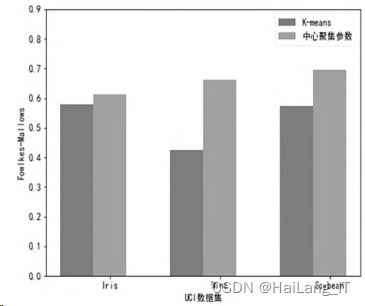
 由图，可以看出基于中心聚 集参数的改进 Ｋ⁃ｍｅａｎｓ 算法得到的相关数值均比 经典 Ｋ⁃ｍｅａｎｓ 聚类算法值要高，并且在 Ｗｉｎｅ 和 Ｓｏｙｂｅａｎ 两个数据集上的表现更为明显。 因此通过 此实验表明，基于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 算 法具有较好的聚类效果。

基于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 协同过 滤推荐算法

把基于中心聚集参数的 改进 Ｋ⁃ｍｅａｎｓ 算法用于协同过滤推荐过程中，为验 证改进后的算法在推荐上的效果，为方便起见，我 们从 ＭｏｖｉｅＬｅｎｓ１００ｋ 数据中随机选取了 １８９ 名用 户的评分数据，并按 ２：８ 分为测试集和训练集，设 计了如下两组对比实验：

实验 １

确定最佳聚类个数。 在这一阶段的 实验中，需要得到两个最佳聚类个数。 首先执行基 于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 算法，得出最佳的 聚类个数是 １９；其次需要判定经典 Ｋ⁃ｍｅａｎｓ 算法的最佳聚类个数，选取的评价指标是平均绝对误差 （ＭＡＥ），当聚类个数以 ２ 为间隔，由 ２ 增加到 ２０ 时，根据 ＭＡＥ 的大小来确定出最佳聚类个数，为了 保证推荐时选取的近邻数相同，将其固定为 ２５，以 此增强 ＭＡＥ 值的可靠性。

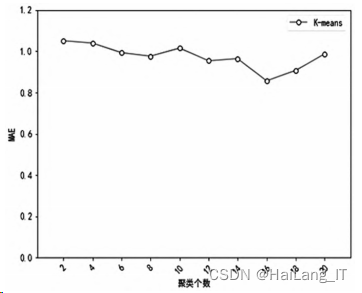
 图表明：随着聚类个数的增加，ＭＡＥ 值呈先 下降后上升趋势，在聚类数 ｋ ＝ １６ 时最低。 因此对 经典 Ｋ⁃ｍｅａｎｓ 算法而言，最佳聚类个数是 １６，从而 保证获取有效的分组，提高在近邻选择时的便利性 和可靠性，取得较好的推荐效果。

实验 ２

推荐算法精度对比。 我们采用三种 算法来做对比试验，分别是：基于中心聚集参数的 改进 Ｋ⁃ｍｅａｎｓ 协同过滤推荐算法、基于 Ｋ⁃ｍｅａｎｓ 的 协同过滤算法与传统的协同过滤推荐算法。 下图 中纵轴是 ＭＡＥ 值，横轴是近邻个数，以 ５ 为间隔从 ５ 增加到 ５０。

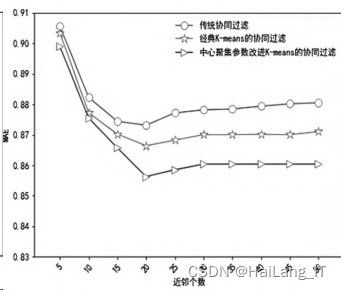
 由图可以看出，进行对比的三种协同过滤推 荐算法它们的 ＭＡＥ 值都呈现先下降后上升的趋 势，整体上随着最近邻个数的增加而降低，且在同样的邻居个数变化的前提下，基于中心聚集参数改 进 Ｋ⁃ｍｅａｎｓ 协同过滤推荐算法的 ＭＡＥ 值最低。 ＭＡＥ 值越低表明推荐误差越小，所以当目标用户 的近邻数不断增加时，推荐准确度也随之提高。 因 此，基于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 协同过滤推 荐算法的推荐效果较好。

四、结论及展望

本文主要从两个角度对个性化推荐系统中的 协同过滤推荐算法进行了优化。 首先，基于 Ｓｌｏｐｅ Ｏｎｅ 算法对缺失数据进行填充，提出了基于 Ｓｌｏｐｅ Ｏｎｅ 的协同过滤推荐优化算法。 其次，提出了一种 基于中心聚集参数的改进 Ｋ⁃ｍｅａｎｓ 优化算法，并将 该算法用于协同过滤推荐中。

实现效果图样例

购物软件的个性化推荐：

我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。

毕设帮助，疑难解答，欢迎打扰！

最后