【数据结构】图论（图的储存方式，图的遍历算法DFS和BFS、图的遍历算法的应用、图的连通性问题）

目录

• 图论
• • 一、 图的基本概念和术语
  • 二、图的存储结构
  • • 1. 数组(邻接矩阵)存储表示
    • • 无向图的数组(邻接矩阵)存储表示
      • 有向图的数组(邻接矩阵)存储表示
      • 邻接表存储表示
      • 有向图的十字链表存储表示
      • 无向图的邻接多重表存储表示
      • 三、图的遍历算法
      • • 图的遍历——深度优先搜索（DFS）
        • 图的遍历——广度优先搜索（BFS）
        • 四、图的遍历算法的应用（无向图）
        • 五、图的连通性问题
        • • 生成树
          • Prim算法
          • Kruskal 算法

            图论

            一、 图的基本概念和术语

            网状结构，逻辑关系多对多

            1. 图：图G由集合V和E组成，记为G=（V，E）。图中的结点称为顶点，V(G)是顶点的非空有穷集；相关的顶点偶对称为边，E(G)是边的有穷集。

            图分为有向图、无向图

            1. 有向图(Digraph)——V(G)是顶点的非空有限集；E(G)是有向边（即弧）的有限集合，弧是顶点的有序对，记，v为弧尾(Tail)，w为弧头(Head)
            2. 无向图(Undigraph)——V(G)是顶点的非空有限集；E(G)是边的有限集合，边是顶点的无序对，记（v, w）或（w, v)，并且（v, w)=(w, v).

               

            1. 顶点：表示数据元素

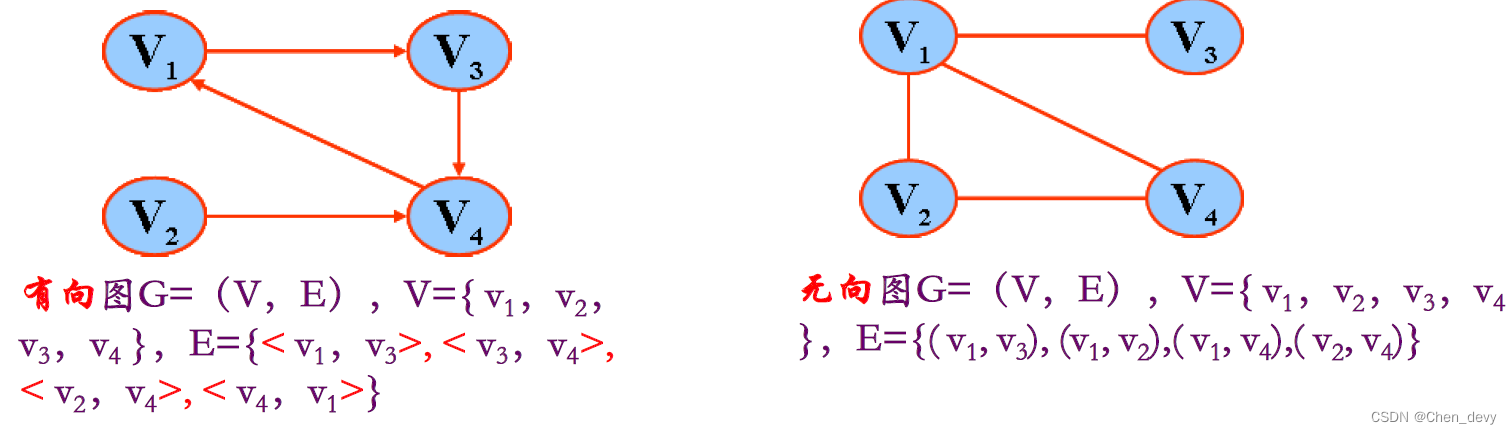
            2. 边：表示数据元素之间的逻辑关系，分为有向边（顶点的有序对）和无向边(顶点的无序对)

            3. 网：边带权的无向图称作无向网；弧带权的有向图称作有向网。

            4. 完全图：n个顶点的含有 n(n-1)/2 条边的无向图称作完全图；n个顶点的含有 e=n(n-1) 条弧的有向图称作 有向完全图.

               若边或弧的个数 e VertexType vexs[MAXSIZE]; //一维数组存放顶点信息 int arcs[MAXSIZE][MAXSIZE];//邻接矩阵 int vexnum, arcnum; //顶点数和边数 int kind; //图的类型：有向图还是无向图 } MGraph; MGraph T; int vex; // 该弧所指向的顶点的位置 struct ArcNode *link; // 指向下一条弧的指针 InfoType *info; // 该弧相关信息的指针 }ArcNode;//单链表节点类型 typedef struct VNode { int data; // 顶点信息 ArcNode *firstarc; // 指向第一条依附该顶点的弧 }VNode;//数组元素类型 typedef struct { VNode arc[MAXSIZE]; int vexnum, arcnum; int kind; //表示有向图还是无向图 }Graphs; // 弧的结构表示 int tailvex, headvex; InfoType *info;//注意定义的类型 struct ArcBox *hlink,*tlink; }ArcBox; typedef structVexNode { // 顶点的结构表示 int data; ArcBox *firstin,*firstout; }VexNode; typedef struct { VexNode xlist[MAXSIZE]; // 顶点信息 int vexnum, arcnum; //有向图的当前顶点数和弧数 }OLGraph; int mark; int ivex, jvex; struct EBox *ilink, *jlink; } EBox; int vex; // 该弧所指向的顶点的位置 struct ArcNode *link; // 指向下一条弧的指针 InfoType *info; // 该弧相关信息的指针 } ArcNode;//单链表节点类型 typedef struct VNode { int data; // 顶点信息 ArcNode *firstarc; // 指向第一条依附该顶点的弧 } VNode;//数组元素类型 typedef struct { VNode arc[MAXSIZE]; int vexnum, arcnum; int kind; //表示有向图还是无向图 } Graphs; int vex; // 该弧所指向的顶点的位置 struct ArcNode *link; // 指向下一条弧的指针 InfoType *info; // 该弧相关信息的指针 } ArcNode;//单链表节点类型 typedef struct VNode { int data; // 顶点信息 ArcNode *firstarc; // 指向第一条依附该顶点的弧 } VNode;//数组元素类型 typedef struct { VNode arc[MAXSIZE]; int vexnum, arcnum; int kind; //表示有向图还是无向图 } Graphs; //深度优先搜索 void DFSTraverse(Graphs G){ for(int v=0;v visited[v]=0; for(v=0;v if(!visited[v]) DFS(G,v); } } } void DFS(Graphs G,int v){ printf("%d\t",v); visited[v]=1; p=G.arc[v].firstarc; while(p){ w=p-vex; if(visited[w]==0) DFS(G,w); p=p-link; } } for(v=0; v int Q[MAX],f=0,r=0; printf("%d\t",w); visited[v]=1; Q[r++]=v; while(f x=Q[f++]; p=G.arc[x].firstarc; while(p){ w=p-vex; if(visited[w]==0){ visited[w]=1; printf("%d\t",w); Q[r++]=w; } p=p-link; } } } int arcs[MAX][MAX]; int vexnum,arcnum; }AGraphs; int arcs[MAX][MAX]; int vexnum,arcnum; }AGraphs; typedef struct{ int adjvex; int lowcost; }EdgeType; /* 当顶点v尚未加入生成树时，closedge[v]存放的是v与生成树中的顶点相连的最好情况：v与生成树中的顶点的所有连边中权值最小的那条边；closedge[v].adjvex存放的这条权值最小的边的另一个顶点，closedge[v].lowcost存放的这条权值最小的边的权值 如何区分生成树中的顶点和不在生成树中的顶点呢？ closedge[w].lowcost==0表示w已经加入生成树 */ void prim(AGraphs G,int u){ int i,j,k; EdgeType closedge[MAX]; for(j=0;j closedge[j].adjvex=u; closedge[j].lowcost=G.arcs[u][j]; } closedge[u].lowcost=0; for(i=1;i k=minclosedge(closedge); printf("(%d,%d)", closedge[k].adjvex,k); closedge[k].lowcost=0; for(j=0;j closedge[j].lowcost= G.arcs[k][j]; closedge[j].adjvex =k; } } } int minclosedge(EdgeType closedge[]){ int min,j,k; min=MAXEDGE; k=-1; for(j=0;j min=closedge[j]. lowcost; k=j; } return k; } //时间复杂度：O(n2) Prim算法适合于稠密图