2024年十五屆藍橋杯省賽大學B組真題(Java)
前言:
賽後一直猶豫要不要對比賽進行複盤出個題解,拖到了現在,終于也是等到比賽結果出來,看到沒有辜負個人期望成功取得省一,決定在國賽前對省賽進行一個複盤,順帶查漏補缺,總體而言,這次JavaB組的省賽題偏基礎,沒有太多的算法,也是延續了暴力杯的頭銜,這次對數學的考察居然比以往提高了不少,令我感到意外,題外話不多說,讓我們一起來複盤一下第十五屆的省賽題吧,同時也祝願各位能取得一個不錯的成績。
(未完篇)
題單鏈接
點擊此處跳轉
試題A:報數遊戲
本題總分:5 分
【問題描述】

【答案提交】
這是一道結果填空的題,你隻需要算出結果後提交即可。本題的結果爲一 個整數,在提交答案時隻填寫這個整數,填寫多餘的内容将無法得分。
答案:2429042904288
【解題思路】
該題數據量大,單純靠電腦跑不太現實,那麽其中肯定有數學規律在,通過計算可以得出 20 和 24 的最小公倍數是 120 ,再對符合條件的前四十個數進行輸出,我們可以發現該規律是十次一循環,每次結尾都是 120 的倍數,那麽我們可以求得第 202420242020 個數的值爲 202420242020/10*120=2429042904240 ,再通過觀察發現第四個數與上一個循環相差 48 ,把兩個數值相加得到答案 2429042904288
【代碼】
package SS2024b.baoshuyouxi;
public class Main {
public static void main(String[] args) {
long n = 202420242024L;
// long count = 0;
// for (long i = 1; count
試題 B: 類斐波那契循環數
本題總分:5 分
【問題描述】

【答案提交】
這是一道結果填空的題,你隻需要算出結果後提交即可。本題的結果爲一 個整數,在提交答案時隻填寫這個整數,填寫多餘的内容将無法得分。
答案:7913837
【解題思路】
給出一個判斷是否爲類斐波那契循環數的判斷式,該判斷式類似于滾動窗口,固定取一個窗口大小,該大小爲 n 的值,維護窗口内所有值的和 sum ,判斷 sum 在小于等于 n 是是否存在相等的情況即可,從 1e7 開始一直遞減遍曆下去,遇到的第一個符合條件的數即爲答案。
【代碼】
package SS2024b.leifeibonaqixunhuan;
import java.util.ArrayList;
public class Main {
public static void main(String[] args) {
int l = (int) 1e7;
while (l > 0) {
if (isLei(l)) {
System.out.println(l);
break;
}
l--;
}
}
static boolean isLei(int n) {
boolean flag = false;
int n1 = n;
ArrayList ys = new ArrayList();
while (n1 != 0) {
ys.add(n1 % 10);
n1 /= 10;
}
ArrayList s = new ArrayList();
s.add(0);
int sum = 0;
for (int i = ys.size() - 1; i >= 0; i--) {
s.add(ys.get(i));
sum += ys.get(i);
}
int index = 0;
while (sum
if (index != 0) {
sum *= 2;
}
s.add(sum -= s.get(index++));
if (sum == n) {
flag = true;
break;
}
}
return flag;
}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
ArrayList
list[i] = new ArrayList
String cz = scan.next();
if (cz.equals("add")) {
int element = scan.nextInt();
list[0].add(element);
} else if (cz.equals("sync")) {
int follower_id = scan.nextInt();
if (list[0].size() != list[follower_id].size()) {
list[follower_id].add(list[0].get(list[follower_id].size()));
}
} else if (cz.equals("query")) {
int min = list[0].size();
for (int i = 1; i
試題 E: 最優分組
時間限制: 3.0s 内存限制: 512.0MB 本題總分:15 分
【問題描述】

【輸入格式】
第一行,一個整數 N。
第二行,一個浮點數 p。
【輸出格式】
輸出一行,一個整數 K 表示答案。
【樣例輸入】
1000
0.05
【樣例輸出】
5
【樣例說明】
無
【評測用例規模與約定】
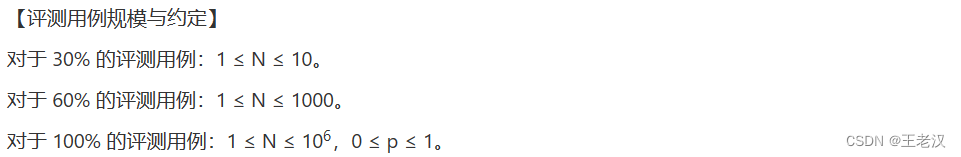
【解題思路】
本題是求解數學期望值,最大期望用試劑量爲 N ,分成每組 k 隻寵物後,生病概率爲 1-(1-p)
k
^k
k ,固定要使用的試劑量爲 n/k ,如果一組寵物生病的額外用試劑量爲 k ,生病的總用試劑量爲 k*[1-(1-p)
k
^k
k]n/k ,則總的期望用試劑量爲 k[1-(1-p)
k
^k
k]*n/k+n/k 利用該式可求得最小期望值所代表的 k 。
【代碼】
package SS2024b.zuiyoufenzu;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
double p = scan.nextDouble();
double min = 1.0 * n;
int min_index = 1;
for (int k = 1; k
if (n % k == 0) {
double num = k * (1 - Math.pow(1 - p, k)) * n / k + n / k;
if (num 








