基于K-means和FCM算法的合成纹理图像及SAR图像的分割

🎀个人主页： https://zhangxiaoshu.blog.csdn.net

📢欢迎大家：关注🔍+点赞👍+评论📝+收藏⭐️，如有错误敬请指正!

💕未来很长，值得我们全力奔赴更美好的生活！

前言

合成纹理图像和SAR（Synthetic Aperture Radar，合成孔径雷达）图像的分割任务在遥感图像处理和计算机视觉领域中具有重要的应用价值。例如对于环境监测、资源管理、灾害应对、国防安全等方面。本文主要介绍基于K均值和模糊C均值算法的合成纹理图像及SAR图像的分割小实例。

文章目录

• 前言
• 介绍
• • 1. 合成纹理图像
  • 2. 分割任务
  • 一、K均值算法以及模糊C均值算法
  • • 1. K均值算法
    • 2. 模糊C均值算法
    • 二、K均值算法以及模糊C均值算法分割实验
    • • 1. K均值算法分割实验
      • 2. 模糊C均值算法分割实验

        ---

        介绍

        1. 合成纹理图像

        1. 合成纹理图像通常是通过人工合成或利用纹理合成算法生成的图像。它们具有多样的纹理特征，用于模拟真实场景中的各种地物表面，如土地覆盖、植被类型等。合成纹理图像在图像分割任务中可以用作训练数据，用于模型的训练和验证。

           SAR图像：

        2. 合成孔径雷达（SAR）是一种主动遥感技术，利用雷达系统发射脉冲信号，接收反射回来的信号，并利用回波数据生成图像。SAR图像通常具有独特的特征，例如对地物形态、材质和湿度等的敏感性，因此在土地利用、资源管理、环境监测等领域具有广泛的应用。SAR图像分割任务的目的是将图像中的不同地物区域进行有效地分割和识别。

        2. 分割任务

        图像分割任务旨在将图像中的像素划分为不同的类别或区域，使得每个区域具有相似的特征或语义含义。在合成纹理图像和SAR图像的分割任务中，目标是将图像中的不同地物或地物类型进行分割，以实现对地物的识别和定量分析。

        1. 合成纹理图像分割任务：旨在将合成纹理图像中的不同地物区域（如建筑、水体、植被等）进行分割，从而实现对地物的识别和分类。

        2. SAR图像分割任务：旨在将SAR图像中的不同地物区域（如建筑、道路、植被等）进行分割，以实现对地物的识别和监测。

        这些分割任务的结果可以为地理信息系统（GIS）、环境监测、城市规划等应用提供重要的数据支持，有助于对地表覆盖类型、土地利用情况、环境变化等进行定量分析和监测。因此，合成纹理图像和SAR图像的分割任务在地学、地理信息科学、遥感技术和环境科学等领域具有广泛的应用前景。

        一、K均值算法以及模糊C均值算法

        1. K均值算法

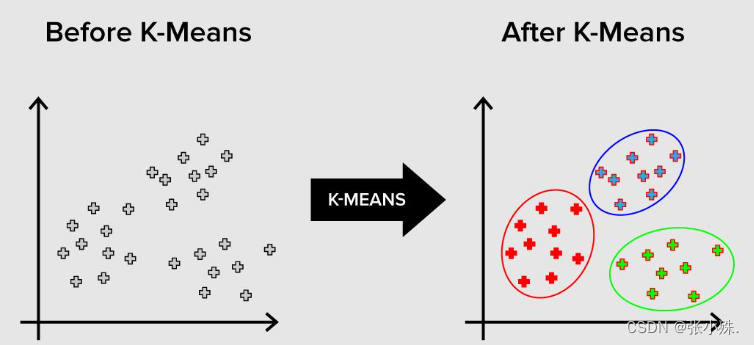
        K均值（K-means）算法是一种经典的聚类算法，用于将数据集分成K个不同的组（簇），使得每个数据点都属于与其最近的簇中心所对应的簇。K均值算法的步骤如下：

        

        • 初始化：随机选择K个初始的簇中心（centroid），可以是数据集中的随机样本或者随机生成的点。

        • 分配：对于每个数据点，计算其与K个簇中心的距离，并将其分配给距离最近的簇中心所对应的簇。

        • 更新：对于每个簇，计算其所有数据点的均值，并将该均值作为新的簇中心。

        • 重复：重复步骤2和步骤3，直到簇中心不再发生变化或者达到最大迭代次数。

        • 收敛：当簇中心不再发生变化时，算法收敛，得到最终的簇划分结果。

          2. 模糊C均值算法

          模糊C均值（FCM，Fuzzy C-means）算法是K均值算法的一种扩展，它允许数据点属于多个簇的可能性，而不是强制将每个数据点分配给一个唯一的簇。这使得FCM算法对于某些数据集的聚类更加灵活和鲁棒。

          算法步骤：

          • 初始化：随机初始化K个簇中心，并为每个数据点分配一个隶属度（membership degree）向量，表示数据点属于每个簇的可能性。

          • 计算簇中心：对于每个簇，计算其簇中心，作为该簇中所有数据点的加权平均值，其中权重由数据点与簇中心的距离以及隶属度来决定。

          • 更新隶属度：根据数据点与各个簇中心之间的距离以及指定的模糊参数m，更新每个数据点的隶属度向量。

          • 检查停止条件：如果隶属度向量的变化小于预先指定的阈值，或者达到最大迭代次数，则停止迭代；否则返回步骤2。

          • 收敛：当满足停止条件时，算法收敛，得到最终的簇中心和每个数据点的隶属度向量。

            二、K均值算法以及模糊C均值算法分割实验

            1. K均值算法分割实验

            算法代码如下所示：

            import cv2
            import numpy as np
            import matplotlib.pyplot as plt
            #读取原始图像
            img = cv2.imread('D:/VSCode/Task_python/lab/homework/Mosaic1_new.tif') 
            #img = cv2.imread('D:/VSCode/Task_python/lab/homework/river_2.bmp')
            data = img.reshape((-1,3))
            data = np.float32(data)
            #定义中心 (type,max_iter,epsilon)
            criteria = (cv2.TERM_CRITERIA_EPS +
                        cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
            #设置标签
            flags = cv2.KMEANS_RANDOM_CENTERS
            #K-Means聚类 聚集成2类
            compactness, labels2, centers2 = cv2.kmeans(data, 2, None, criteria, 10, flags)
            #图像转换回uint8二维类型
            centers2 = np.uint8(centers2)
            res = centers2[labels2.flatten()]
            dst2 = res.reshape((img.shape))
            #图像转换为gray显示
            img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
            dst2 = cv2.cvtColor(dst2, cv2.COLOR_BGR2GRAY)
            #用来正常显示中文标签
            plt.rcParams['font.sans-serif']=['SimHei']
            #显示图像
            titles = [u'原始图像', u'kmeans聚类图像 K=2'] 
            images = [img, dst2] 
            for i in range(2): 
             plt.subplot(1,2,i+1), plt.imshow(images[i], 'gray'), 
             plt.title(titles[i]) 
             plt.xticks([]),plt.yticks([]) 
            plt.savefig('D:/VSCode/Task_python/lab/homework/kmeans_1.jpg')
            plt.show()
            

            结果如下图所示：

            

            

            2. 模糊C均值算法分割实验

            算法代码如下所示：

            import numpy as np
            import matplotlib.pyplot as plt
            import time
            import cv2
            star = time.time()  # 计时
            #img = cv2.imread('D:/VSCode/Task_python/lab/homework/Mosaic1_new.tif')  # 读取图片信息，存储在一个三维数组中
            img = cv2.imread('D:/VSCode/Task_python/lab/homework/river_2.bmp')
            row = img.shape[0]
            col = img.shape[1]
            plt.figure(1)
            plt.figure(figsize=(9, 7))
            plt.subplot(221)
            plt.title('原始图像')
            plt.imshow(img)
             
             
            def fcm(data, threshold, k, m):
                # 0.初始化
                data = data.reshape(-1, 3)
                cluster_center = np.zeros([k, 3])  # 簇心
                distance = np.zeros([k, row*col])  # 欧氏距离
                times = 0  # 迭代次数
                goal_j = np.array([])  # 迭代终止条件：目标函数
                goal_u = np.array([])  # 迭代终止条件：隶属度矩阵元素最大变化量
                # 1.初始化U
                u = np.random.dirichlet(np.ones(k), row*col).T  # 形状（k, col*rol），任意一列元素和=1
                #  for s in range(50):
                while 1:
                    times += 1
                    print('循环：', times)
                    # 2.簇心update
                    for i in range(k):
                        cluster_center[i] = np.sum((np.tile(u[i] ** m, (3, 1))).T * data, axis=0) / np.sum(u[i] ** m)
                    # 3.U update
                    # 3.1欧拉距离
                    for i in range(k):
                        distance[i] = np.sqrt(np.sum((data - np.tile(cluster_center[i], (row * col, 1))) ** 2, axis=1))
                    # 3.2目标函数
                    goal_j = np.append(goal_j, np.sum((u**m)*distance**2))
                    # 3.3 更新隶属度矩阵
                    oldu = u.copy()  # 记录上一次隶属度矩阵
                    u = np.zeros([k, row * col])
                    for i in range(k):
                        for j in range(k):
                            u[i] += (distance[i] / distance[j]) ** (2 / (m - 1))
                        u[i] = 1/u[i]
                    goal_u = np.append(goal_u, np.max(u - oldu))  # 隶属度元素最大变化量
                    print('隶属度元素最大变化量', np.max(u - oldu), '目标函数', np.sum((u**m)*distance**2))
                    # 4.判断：隶属度矩阵元素最大变化量是否小于阈值
                    if np.max(u - oldu)