爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
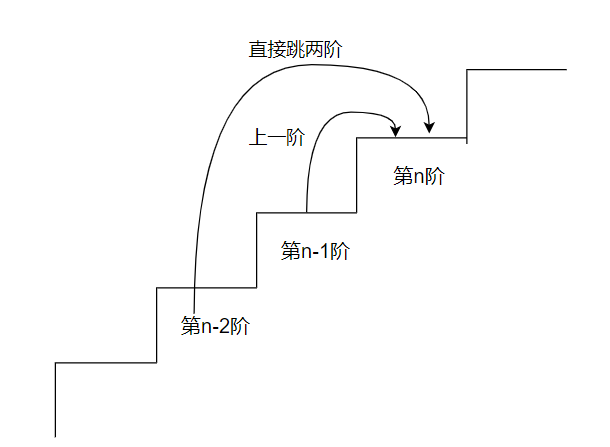
(图片来源网络,侵删)
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
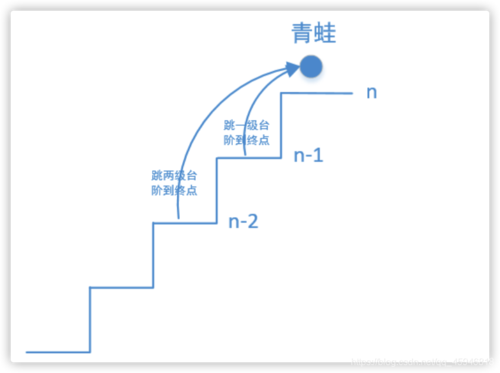
(图片来源网络,侵删)
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
解题思路
- 1、使用动态规划,定义一个数组dp,其中dp[i]表示到达第i阶楼梯的不同方法数。
- 2、初始化dp[0]和dp[1]为1,分别表示到达第0阶和第1阶楼梯的方法数为1。
- 3、对于每一阶楼梯i,有两种方式到达:从第i-1阶楼梯爬1步,或者从第i-2阶楼梯爬2步。
- 4、因此,动态规划方程为:dp[i] = dp[i - 1] + dp[i - 2]。
- 5、最终返回dp[n],即到达第n阶楼梯的不同方法数。
Java实现
public class ClimbingStairs { public static int climbStairs(int n) { if (n return n; } int[] dp = new int[n + 1]; dp[1] = 1; dp[2] = 2; for (int i = 3; i dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; } public static void main(string[] args) { // int n1 = 2; // System.out.println(climbStairs(n1)); // Output: 2 // // int n2 = 3; // System.out.println(climbStairs(n2)); // Output: 3 int n8 = 8; System.out.println(climbStairs(n8)); // Output: 34 } }









