基础算法---前缀和

文章目录

• 基本思想
• 1.前缀和
• 2.子矩阵的和
• 3.长度最小的子数组
• 4，除自身以外数组的乘积
• 总结

  

  基本思想

  前缀和数组就是一个数组的前i项和

  

  

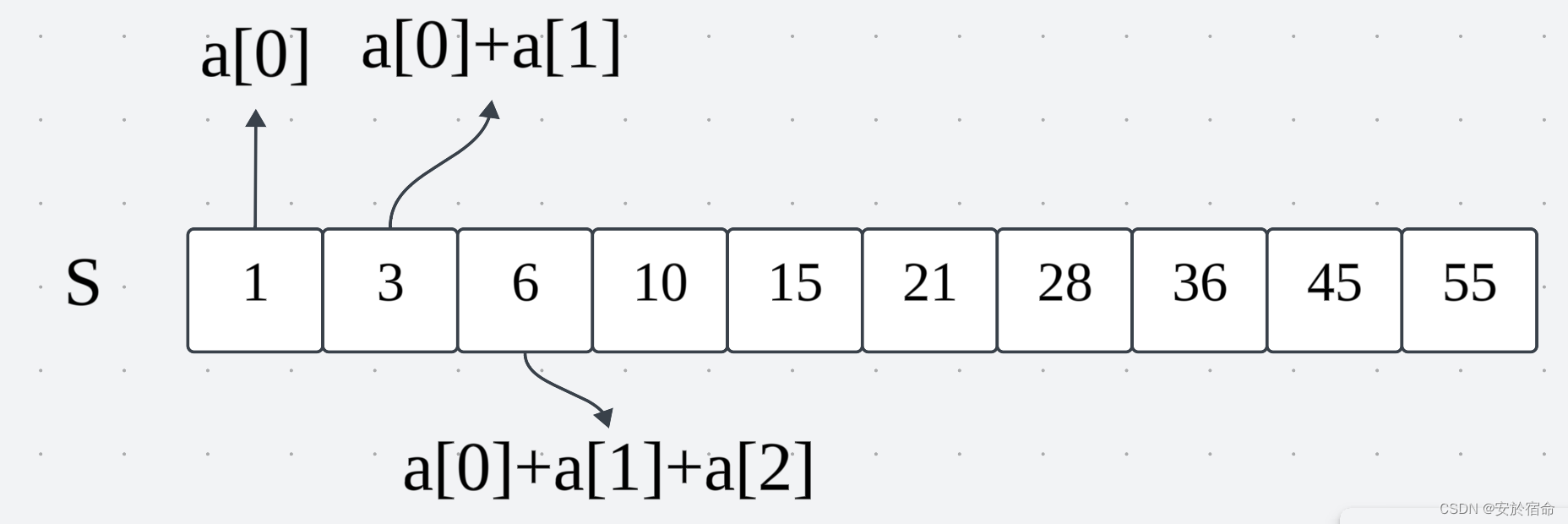
  前缀和的用处：前缀和数组求出来之后我们就可以就可以求数组中的某个特定区间的和

  

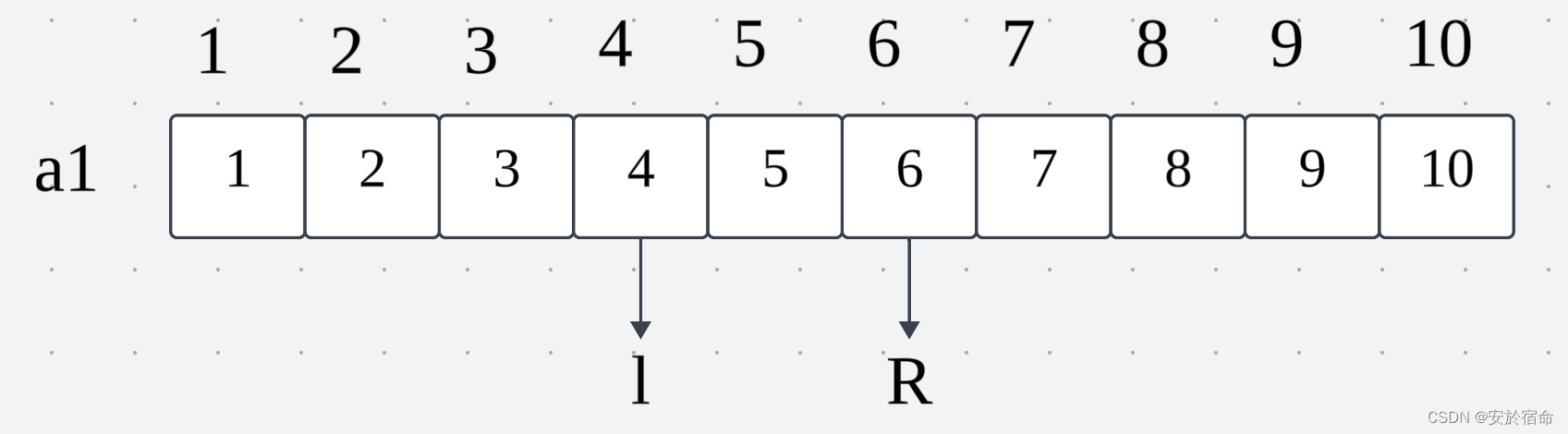
  就比如说求l到R的和，我们可以转换为求1到R的和减去1到l-1的和

  接下来我们来做两道题，让大家感受一下

  1.前缀和

  这道题是一道非常经典最能代表前缀和算法的一道题

  

  这道题的思路很简单就是根据公式s[i]=s[i-1]+a[i]然后将前缀和求出来，根据条件去输出，我们来看一下代码

  #include
  using namespace std;
  #define N 100010
  //n个数据和m行
  int n,m;
  //定义一个数组和一个前缀和数组
  int a[N],S[N];
  //定义两个边界
  int l,r;
  int main()
  {
  	//输入
      cin>>n>>m;
      //输入
      for(int i=1;i>a[i];
      //将前缀和的s[0]定义为0，这样方便求出第多少到第多少的和
      S[0]=0;
      //根据公式求出前缀和
      for(int i=1;i
          S[i]=S[i-1]+a[i];
      }
      //根绝条件输出
      while(m)
      {
          cin>l>>r;
          cout
      cinnm>>q;
      for(int i=1;i
          for(int j=1;j
              cina[i][j];
          }
      }
      for(int i=1;i
          for(int j=1;j
              s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
          }
      }
      while(q--)
      {
          int x1,x2,y1,y2;
          cinx1>>y1>>x2>>y2;
          cout
      int *S=(int*)malloc(sizeof(int)*(numsSize+1));
      S[0] = 0;
      for (int i = 1;i 
          S[i] = S[i - 1] + nums[i - 1];
      }
      int min = 0;
      int l = 0;
      int r = 1;
      while (r  
  总结
   
  在本文中，我们深入探讨了前缀和算法的原理、应用以及实现方式。通过对前缀和的定义和性质的理解，我们可以更有效地解决一系列问题，特别是那些涉及连续子数组和区间求和的场景。通过将原始数据预处理成前缀和数组，我们能够在常数时间内快速地回答各种查询，从而大大提高了算法的效率。
   
  我们讨论了如何应用前缀和算法解决了几个实际问题，例如求解子数组和的最大值、最小值，以及计算区间和等。这些问题在实际应用中经常遇到，而前缀和算法为我们提供了一种高效的解决方案。
   
  此外，我们还介绍了如何通过巧妙地利用前缀和数组，解决了一些其他类型的问题，例如寻找具有特定和值的子数组个数、寻找具有特定和值的子数组的起始位置等。
   
  总的来说，前缀和算法是一种非常强大且实用的技术，可以广泛应用于解决各种问题，包括算法竞赛、编程面试以及实际工程项目中。通过深入理解前缀和算法的原理和应用，我们可以在算法设计和问题求解中发挥更大的作用，提高代码的效率和性能。希望本文对读者对前缀和算法有所启发，并能够在实践中加以运用。