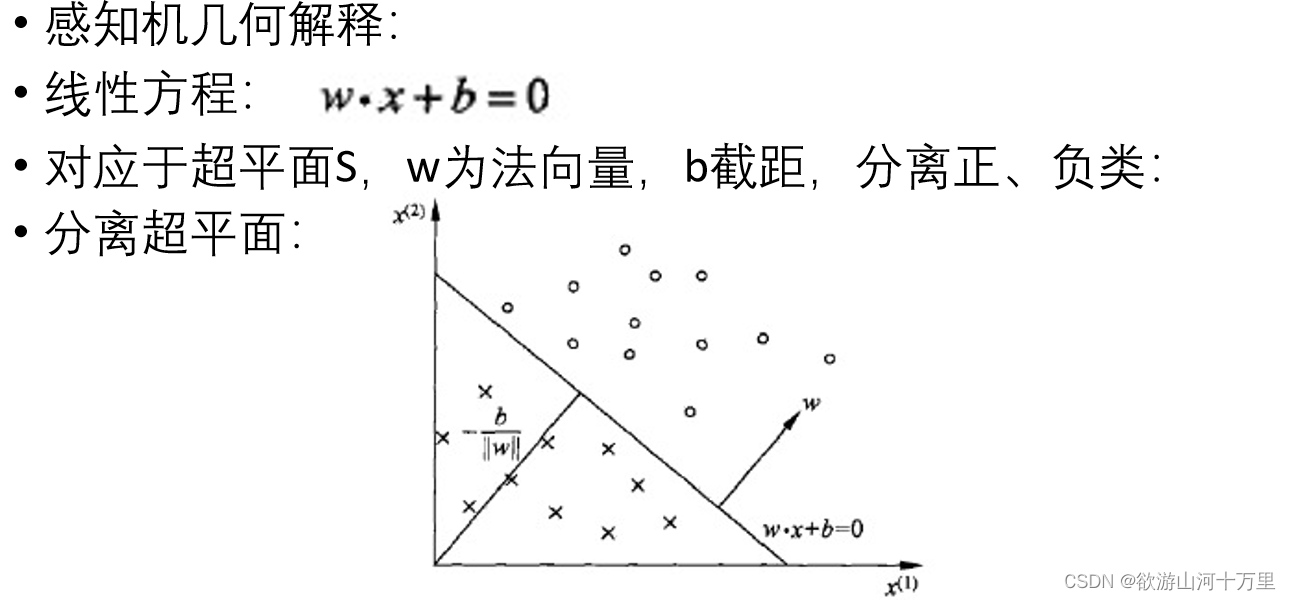
本章节主要介绍感知机的基础知识,虽然在目前的机器学习范围内,感知机已经不怎么使用,但是通过对感知机的学习可以更好的了解以后的线性模型等相关知识。
同时读者可以点击链接:机器学习-目录_欲游山河十万里的博客-CSDN博客
学习完整的机器学习的相关知识。
目录
感知机
一、感知机的学习目标
二、感知机的介绍
2.1感知机模型
2.2感知机损失函数的定义
2.3简单的理解感知机的原理
2.4感知机结构介绍
2.4.1简单的逻辑电路
三、感知机的引入
3.1 线性可分和线性不可分
3.2感知机模型分析
四、感知机原始形式(鸢尾花分类)
4.1数据集的准备
4.1.1导入包
4.1.2导入数据集
4.1.3原始数据可视化
4.1.4划分数据集和标签
4.1.5感知机的实现
4.2感知机原始形式(鸢尾花分类)
4.2.1导入模块
4.2.2自定义感知机模型
4.2.3获取数据
参考文献
写在最后
感知机
感知机在1957年被提出,算是最古老的分类方法之一。
虽然感知机泛化能力不及其他的分类模型,但是如果能够对感知机的原理有一定的认识,在之后学习支持向量机、神经网络等机器学习算法的时候会轻松很多。
一、感知机的学习目标
- 感知机模型
- 感知机的损失函数和目标函数
- 感知机原始形式和对偶形式
- 感知机流程
- 感知机优缺点
二、感知机的介绍
在本部分,我参考了网上多位博文对感知机的不同理解,大家可以根据自己的喜好进行对应的理解。
输入为实例的特征向量,输出为实例的类别,取+1和-1;
感知机对应于输入空间中将实例划分为正负两类的分离超平面,属于判别模型;
导入基于误分类的损失函数; 利用梯度下降法对损失函数进行极小化;
感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式;
1957年由Rosenblatt提出,是神经网络与支持向量机的基础。
2.1感知机模型
2.2感知机损失函数的定义


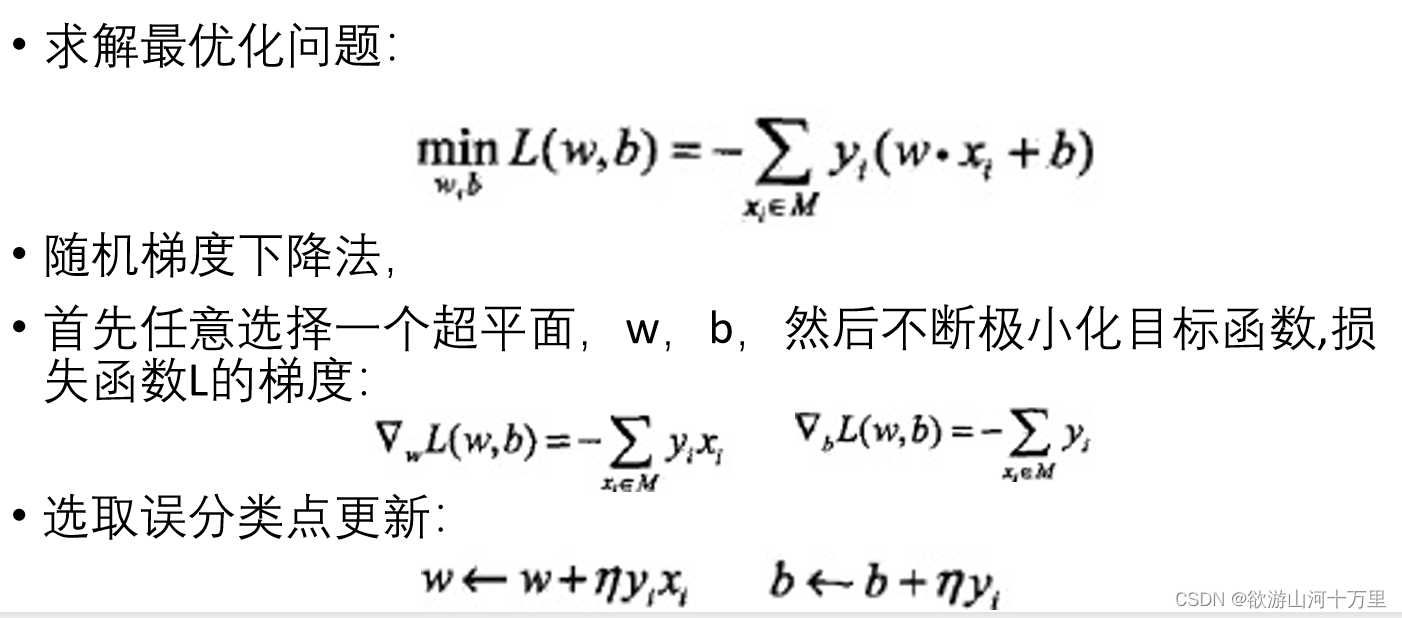
2.3简单的理解感知机的原理
1.感知机是根据输入实例的特征向量对其进行二类分类的线性分类模型:
感知机模型对应于输入空间(特征空间)中的分离超平面。
2.感知机学习的策略是极小化损失函数:
求出L最小数值时候的,w,b的值
损失函数对应于误分类点到分离超平面的总距离。
3.感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法,有原始形式和对偶形式。算法简单且易于实现。原始形式中,首先任意选取一个超平面,然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。
4.当训练数据集线性可分时,感知机学习算法是收敛的。感知机算法在训练数据集上的误分类次数满足不等式:
当训练数据集线性可分时,感知机学习算法存在无穷多个解,其解由于不同的初值或不同的迭代顺序而可能有所不同。
2.4感知机结构介绍
感知机接收多个输入信号,输出一个信号。感知机的信号只有“流/不流”(1/0)两种取值。0对应“不传递信号”,1对应“传递信号”。

----上图是一个接收两个输入信号的感知机的例子。x1、x2是输入信号,y是输出信号,w1、w2是权重(w是weight的首字母)。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重(w1x1、w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活”。这里将这个界限值称为阈值,用符号θ表示。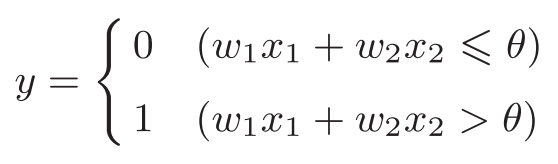
----感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性就越高。
----权重相当于电流里所说的电阻。电阻是决定电流流动难度的参数,电阻越低,通过的电流就越大。而感知机的权重则是值越大,通过的信号就越大。不管是电阻还是权重,在控制信号流动难度(或者流动容易度)这一点上的作用都是一样的。
下面开始举一些简单的例子并通过python语言实现这些案例
2.4.1简单的逻辑电路
与门

与非门和或门(NAND gate)
----与非门就是颠倒了与门的输出。仅当x1和x2同时为1时输出0,其他时候则输出1。
与非真值表

或门的表

下面开始代码的具体实现操作。
import numpy as np
def AND(x1,x2):#与门操作,需要x1和x2全部为1的情况下,才可以输出1
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp