目录
一、说明
二、图卷积网络
三、图卷积网络是如何工作的？
四、如何手动计算图卷积网络（GCN）？
4.1 构建网络
4.2 开始执行训练（参见上图）
五、图卷积网络的应用
一、说明
图卷积网络 （GCN） 于 2017 年推出，已成为分析和解释结构为图的数据的强大工具。对于非线性的关系，如拓扑形结构，CNN将出现规模上的爆炸，因此，这里涌现出了很多方法，例如GNN、DeepWalk、node2vec等等，GCN只是其中一种，这里只讲GCN，其他的后面有空再讨论。
二、图卷积网络
GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding），可见用途广泛。因此现在人们脑洞大开，让GCN到各个领域中发光发热。
图卷积网络 （GCN） 是处理图结构数据的神经网络架构。想象一下，你有一组对象（节点）通过关系（边）连接，形成一个网络。GCN旨在通过分析节点之间的关系来学习这种网络结构。
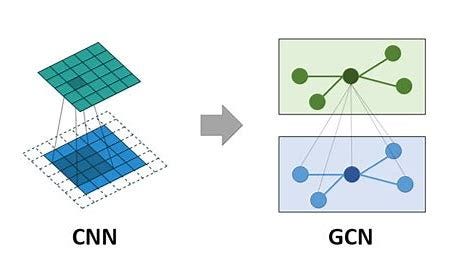
将 GCN 视为强大的模式识别工具，用于扫描图中节点的局部邻域。就像卷积神经网络 （CNN） 扫描图像中的局部邻域一样，GCN 扫描图形中的局部邻域。
GCN 学习根据不同节点与相邻节点的关系为它们分配重要性。他们学会关注图结构中的模式，这些模式对给定任务有信息，例如对节点进行分类或预测节点之间的关系。
三、图卷积网络是如何工作的？
图卷积网络 （GCN） 是设计用于处理图结构数据的神经网络，其中节点（对象）通过边（关系）连接。它们的工作方式类似于卷积神经网络 （CNN），后者用于图像处理。
将图形想象成一组由边缘连接的节点，就像一个社交网络，其中节点代表人，边缘代表友谊。GCN 通过聚合来自相邻节点的信息来学习“卷积”每个节点周围的信息。
图卷积网络
- 数据准备：以适合 GCN 的格式表示图形。这涉及将图转换为节点邻接矩阵 （A） 和节点特征矩阵 （X）。邻接矩阵描述图拓扑，而特征矩阵包含节点属性。
- 卷积运算：GCN 使用可学习的权重矩阵对节点特征矩阵执行卷积运算。这些卷积运算是专门为图形设计的，与图像处理中使用的二维卷积不同。
- 非线性激活：GCN 将非线性激活函数应用于卷积节点特征，使它们能够学习更复杂的表示。
- 训练和预测：GCN 在监督学习任务（例如节点分类或链路预测）期间使用反向传播进行训练。经过训练后，GCN 可用于按照相同的步骤对新的图形结构数据进行预测。
简单来说，图卷积网络的工作原理是通过聚合来自相邻节点的信息来学习“卷积”每个节点周围的信息。这些网络是为图结构数据而设计的，当理解图中节点之间的关系很重要时，这些网络特别有用。
图卷积网络
四、如何手动计算图卷积网络（GCN）？
本练习演示了 GCN 如何在一个简单的应用程序中工作：二元分类。
4.1 构建网络
预测图形中的节点是否为 X。
1）建立两层GCN层（与CNN类似）
🟪 图卷积网络 （GCN）
1.GCN1（4,3）
2.GCN2（3,3）
2）连接层
🟦 全连接网络 （FCN）
1.线性1（3,5）
2.ReLU
3.线性2（5,1）
4. sigmoid
3) 简单化
• 相邻矩阵未归一化。
• ReLU 直接应用于消息。
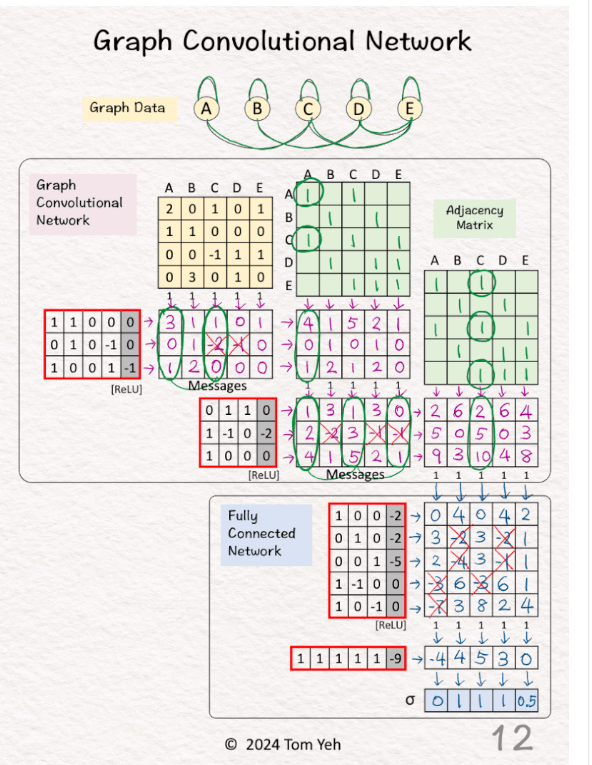图卷积网络 作者：Tom 教授
4.2 开始执行训练（参见上图）
[1] 给定
↳ 具有五个节点 A、B、C、D、E 的图形
[2] 🟩 邻接矩阵：邻域
↳ 为邻域的每条边加 1
↳ 在两个方向上重复（例如，A->C、C->A）
↳ 对两个 GCN 层重复
[3] 🟩 邻接矩阵：自
↳ 为每个自循环添加 1
↳ 等效于添加恒等矩阵
↳ 对两个 GCN 层重复
[4] 🟪 GCN1：消息
↳ 将节点嵌入🟨与权重和偏差相乘
↳ 应用 ReLU（负数 → 0）
↳ 结果是每个节点一条消息
[5] 🟪 GCN1：池
化↳ 将消息与相邻矩阵相乘
↳ 目的是池化来自每个节点的邻居以及节点本身的消息。
↳ 结果是每个节点都有一个新功能
[6] 🟪 GCN1：可视化
↳ 对于节点 1，可视化消息如何汇集以获得新功能以便更好地理解
↳ [3,0,1] + [1,0,0] = [4,0,1]
[7] 🟪 GCN2：消息
↳ 将节点特征与权重和偏差相乘
↳ 应用 ReLU（负数 → 0）
↳ 结果是每个节点一条消息
[8] 🟪 GCN2：池
化↳ 将消息与相邻矩阵
相乘↳ 结果是每个节点都有一个新功能
[9] 🟪 GCN2：可视化
↳ 对于节点 3，可视化消息如何汇集以获得新功能以便更好地理解
↳ [1,2,4] + [1,3,5] + [0,0,1] = [2,5,10]
[10] 🟦 FCN：线性 1 + ReLU
↳ 使用权重和偏差乘以节点特征
↳ 应用 ReLU（负数 → 0）
↳ 结果是每个节点
都有一个新特征↳ 与 GCN 层不同，不包含来自其他节点的消息。
[11] 🟦 FCN：线性 2
↳ 使用权重和偏差对节点特征进行乘法
[12] 🟦 FCN：Sigmoid
↳ 应用 Sigmoid 激活函数
↳ 目的是获得每个节点
的概率值↳ 手动✍️计算 Sigmoid 的一种方法是使用以下近似值：
• >= 3 → 1
• 0 → 0.5
•
