贪心算法|1005.K次取反后最大化的数组和

力扣题目链接

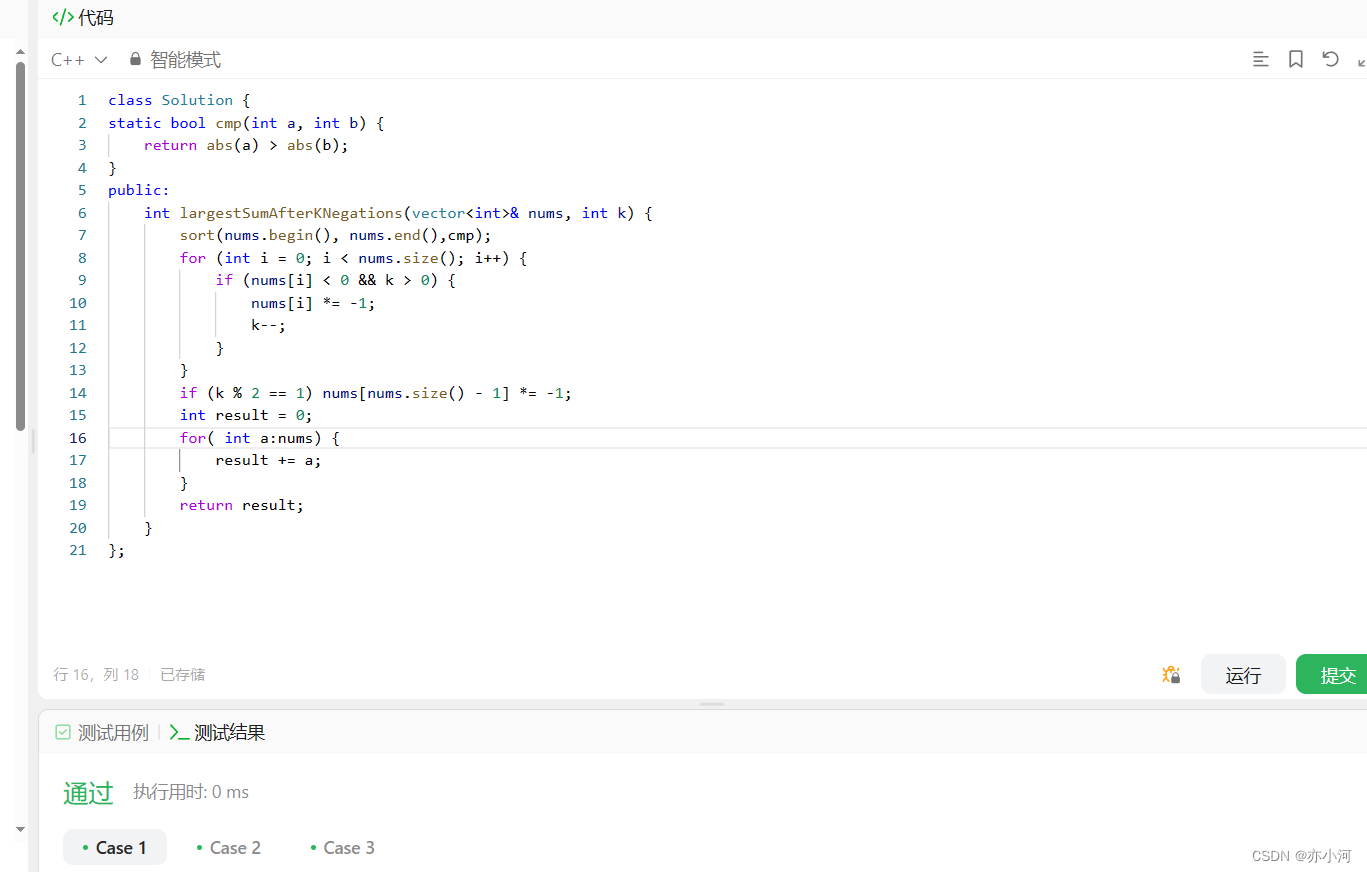
class Solution {
static bool cmp(int a, int b) {
    return abs(a) > abs(b);
}
public:
    int largestSumAfterKNegations(vector& A, int K) {
        sort(A.begin(), A.end(), cmp);       // 第一步
        for (int i = 0; i  0) {
                A[i] *= -1;
                K--;
            }
        }
        if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
        int result = 0;
        for (int a : A) result += a;        // 第四步
        return result;
    }
};

有没有不理解的语法知识呢？

http://t.csdnimg.cn/gC8Is

sort函数中的比较函数cmp()，即void sort( iterator start, iterator end, StrictWeakOrdering cmp );

sort函数头文件为：#include

其中，cmp函数可以自己编写，自己决定逻辑，包括cmp的命名也是自己决定的。

示例如下：

bool cmp(int a ,int b)
{
	return a  就是从大到小 
}
sort(p.begin(), p.end(), cmp);

 代码随想录 (programmercarl.com)

思路

本题思路其实比较好想了，如何可以让数组和最大呢？

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。

虽然这道题目大家做的时候，可能都不会去想什么贪心算法，一鼓作气，就AC了。

我这里其实是为了给大家展现出来 经常被大家忽略的贪心思路，这么一道简单题，就用了两次贪心！

那么本题的解题步骤为：

• 第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
• 第二步：从前向后遍历，遇到负数将其变为正数，同时K--
• 第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
• 第四步：求和

  自己的思路：

  1.求K次取反后的最大和，贪心负数最小的先取反。所以先将数组的绝对值从大到小排序。

  2.遍历

  if (A[i]  0) {
                  A[i] *= -1;
                  K--;
              }

  3.当数组全部为正数时，还存在k为奇数时，贪心，将 最小的正数取反

  4.全部累加