目录
- 【内容介绍】动手学深度学习-基于pytorch版本
- 【脉络梳理】
- 预备知识
- 数据操作
- 数据预处理
- 线性代数
- 矩阵计算
- 自动求导
- 线性神经网络
- 线性回归
- 深度学习的基础优化算法
- 线性回归的从零开始实现
- 线性回归的简洁实现
- Softmax回归
- 损失函数
- 图像分类数据集
- Softmax回归的从零开始实现
- Softmax回归的简洁实现
- 多层感知机
- 感知机
- 多层感知机
- 多层感知机的从零开始实现
- 多层感知机的简洁实现
- 模型选择
- 过拟合和欠拟合
- 权重衰退
- 暂退法(Dropout)
- 数值稳定性
- 模型初始化和激活函数
- 深度学习计算
- 层和块
- 参数管理
- 自定义层
- 读写文件
- 卷积神经网络
- 从全连接层到卷积
- 图像卷积
- 填充和步幅
- 多输入多输出通道
- 池化层(汇聚层)
- LeNet
- 现代卷积神经网络
- 深度卷积神经网络(AlexNet)
- 使用块的网络(VGG)
- 网络中的网络(NiN)
- 含并行连结的网络(GoogLeNet)
- 批量规范化(归一化)
- 残差网络(ResNet)
- 计算性能
- 深度学习硬件(CPU和GPU)
- 深度学习硬件(TPU和其他)
- 单机多卡并行
- 分布式训练
- 计算机视觉
- 图像增广
- 微调
- 物体检测和数据集
- 锚框
- 物体检测算法:R-CNN,SSD,YOLO
- 单发多框检测(SSD)
- YOLO
- 语义分割
- 转置卷积
- 全连接卷积神经网络 FCN
- 样式迁移
- 循环神经网络
- 序列模型
- 语言模型
- 循环神经网络
- 现代循环神经网络
- 门控循环单元GRU
- 长短期记忆网络(LSTM)
- 深度循环神经网络
- 双向循环神经网络
- 编码器-解码器
- 序列到序列学习
- 束搜索
- 注意力机制
- 注意力分数
- 使用注意力机制的seq2seq
- 自注意力
- Transformer
- 自然语言处理:预训练
- BERT预训练
- 自然语言处理:应用
- BERT微调
- 优化算法
- 优化算法
【内容介绍】动手学深度学习-基于pytorch版本
你好! 这是【李沐】动手学深度学习v2-基于pytorch版本的学习笔记
教材
源代码
安装教程(安装pytorch不要用pip,改成conda,pip太慢了,下载不下来)
个人推荐学习学习笔记
【脉络梳理】
预备知识
数据操作
本节代码文件在源代码文件的chapter_preliminaries/ndarray.ipynb中
- 创建数组
创建数组需要:
①形状
②每个元素的数据类型
③每个元素的值
- 访问元素
①一个元素:[1,2]
②一行:[1,:]
③一列:[:,1]
④子区域:[1:3,1:] #第1到2行,第1到最后1列
⑤子区域:[::3,::2] #从第0行开始,每3行一跳,从第0列开始,每2列一跳。
数据预处理
本节代码文件在源代码文件的chapter_preliminaries/pandas.ipynb中
- reshape函数
使用reshape函数后不指向同一块内存,但数据改变是同步的
import torch a=torch.arange(12) b=a.reshape((3,4)) b[:]=2 # 改变b,a也会随之改变 print(a) # tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) a[:]=1 # 改变a,b也会随之改变 print(b) # tensor([[1, 1, 1, 1],[1, 1, 1, 1],[1, 1, 1, 1]]) print(id(b)==id(a)) # False # 但a、b内存不同 print(id(a)) # 2157597781424 print(id(b)) # 2157597781424
线性代数
本节代码文件在源代码文件的chapter_preliminaries/linear-algebra.ipynb中
- 张量的按元素操作
标量、向量、矩阵和任意数量轴的张量(统称为张量)有一些实用的属性。 例如,你可能已经从按元素操作的定义中注意到,任何按元素的一元运算都不会改变其操作数的形状。 同样,给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。
例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行按元素加法;两个矩阵的按元素乘法称为Hadamard积(Hadamard product)(数学符号 ⨀ \bigodot ⨀)。 对于矩阵 A ∈ R m n , B ∈ R m n \bf A\in\mathbb R^{mn},\bf B\in\mathbb R^{mn} A∈Rmn,B∈Rmn, 其中第 i \it i i行和第 j \it j j列的元素是 b i j b_{ij} bij。 矩阵 A \bf A A和 B \bf B B的Hadamard积为
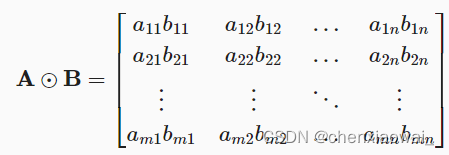
import torch A = torch.arange(20, dtype=torch.float32).reshape(5, 4) B = A.clone() # 通过分配新内存,将A的一个副本分配给B print(A) #tensor([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]) print(A+B) #tensor([[ 0., 2., 4., 6.],[ 8., 10., 12., 14.],[ 16., 18., 20., 22.],[24., 26., 28., 30.],[32., 34., 36., 38.]]) print(A*B) #tensor([[0., 1., 4., 9.],[16., 25., 36., 49.],[64., 81., 100., 121.],[144., 169., 196., 225.],[256., 289., 324., 361.]])
- 降维求和
①原始shape:[5,4]
· axis=0 sum:[ 4 ]
· axis=1 sum:[ 5 ]
②原始shape:[2,5,4]
· axis=1 sum:[2,4]
· axis=2 sum:[2,5]
· axis=[1,2] sum:[ 4 ]
- 非降维求和
原始shape:[2,5,4] 参数 keepdims=True
· axis=1 sum:[2,1,4]
· axis=1 sum:[2,1,1]
矩阵计算
本节代码文件在源代码文件的chapter_preliminaries/calculus.ipynb中
-
将导数拓展到向量
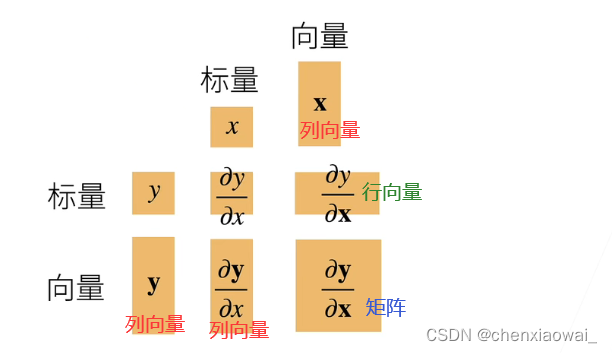
-
标量对列向量求导
其中, a 不是关于 x 的函数, 0 和 1 是向量 ; 其中,\it a不是关于\bf x的函数,\color{black} 0和\bf 1是向量; 其中,a不是关于x的函数,0和1是向量;

-
列向量对列向量求导
结果是矩阵
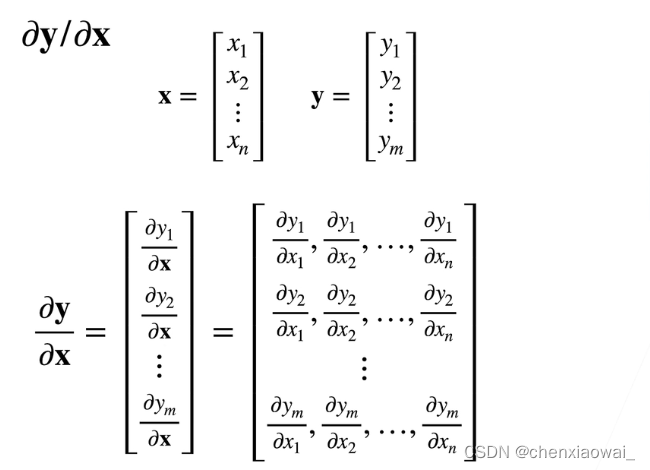
样例:
x ∈ R n , y ∈ R m , ∂ y ∂ x ∈ R m n ; a , a 和 A 不是关于 x 的函数, 0 和 I 是矩阵 ; \bf x\in\mathbb R^{n} ,\bf y\in\mathbb R^{m},\frac{\partial\bf y}{\partial\bf x}\in\mathbb R^{mn};\it a,\bf a和\bf A不是关于\bf x的函数,\color{black} 0和\bf I是矩阵; x∈Rn,y∈Rm,∂x∂y∈Rmn;a,a和A不是关于x的函数,0和I是矩阵;

-
将导数拓展到矩阵

自动求导
本节代码文件在源代码文件的chapter_preliminaries/autograd.ipynb中
- 向量链式法则
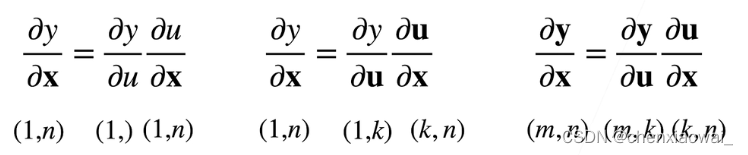
样例:

- 自动求导的两种模式

- 反向累积模式
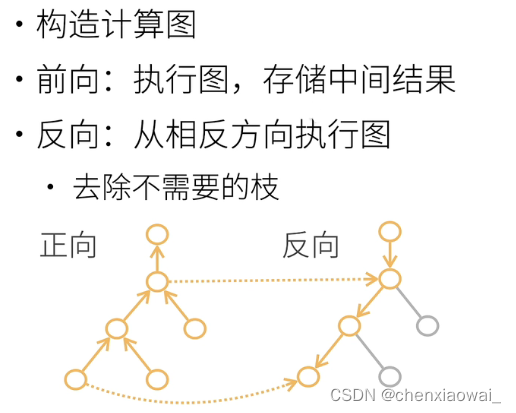
样例:
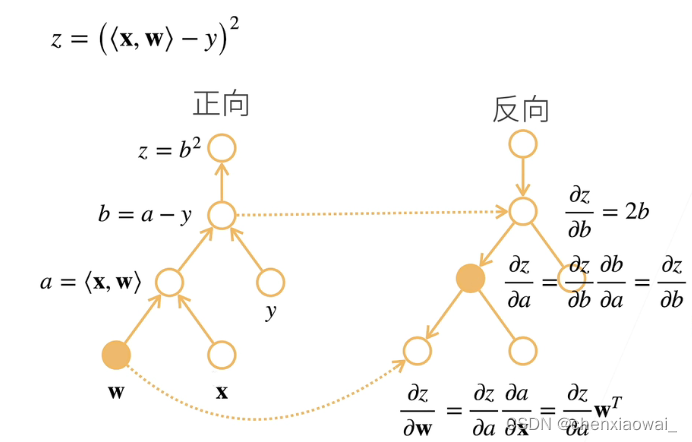
- 正向累积与反向累积复杂度比较
正向累积内存复杂度为O(1),反向累积内存复杂度为O(n);但神经网络通常不会用正向累积,因为正向累积每计算一个变量的梯度都需要扫一遍,计算复杂度太高。

线性神经网络
线性回归
本节代码文件在源代码文件的chapter_linear-networks/linear-regression.ipynb中
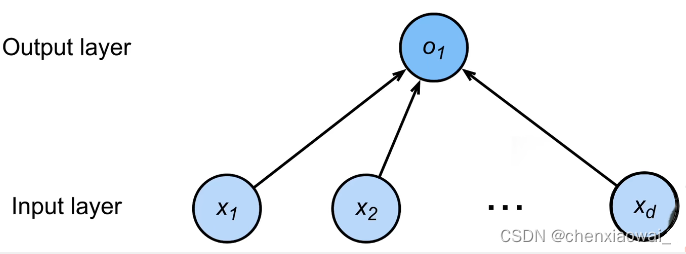
- 线性模型

线性模型可以看做是单层神经网络:
衡量预估质量(损失函数):

- 训练数据

- 参数学习
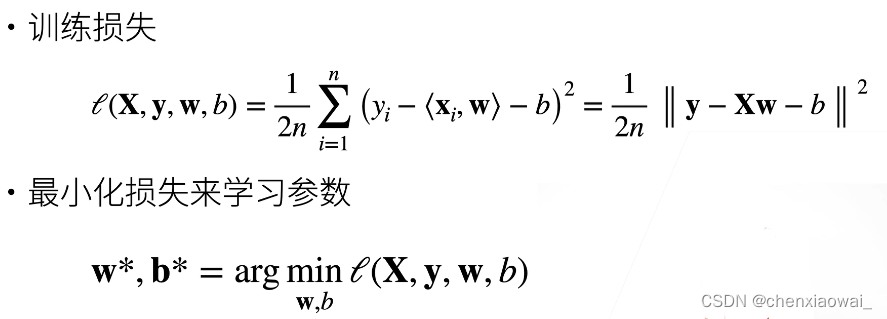
显示解:

- 总结

深度学习的基础优化算法
- 梯度下降
通过不断地在损失函数递减的方向上更新参数来降低误差。

学习率不能太大也不能太小:
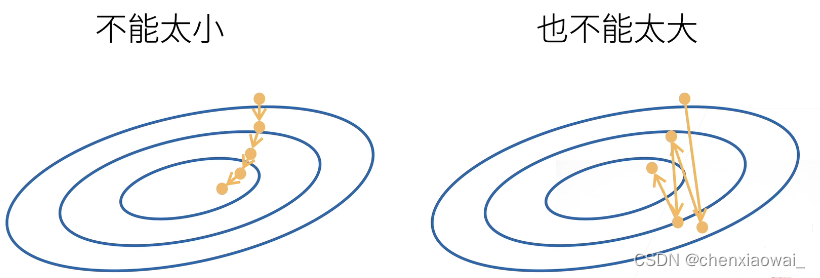
- 小批量随机梯度下降

批量大小不能太大也不能太小:

- 总结

线性回归的从零开始实现
本节代码文件在源代码文件的chapter_linear-networks/linear-regression-scratch.ipynb中
- 实现流程
其中,定义模型包括定义损失函数和定义优化算法
线性回归的简洁实现
本节代码文件在源代码文件的chapter_linear-networks/linear-regression-concise.ipynb中
简洁实现是指通过使用深度学习框架来实现线性回归模型,具体流程与从零开始实现大体相同,不过一些常用函数不需要我们自己写了(直接导库,用别人写好的)
- 实现流程
Softmax回归
本节代码文件在源代码文件的chapter_linear-networks/softmax-regression.ipynb中
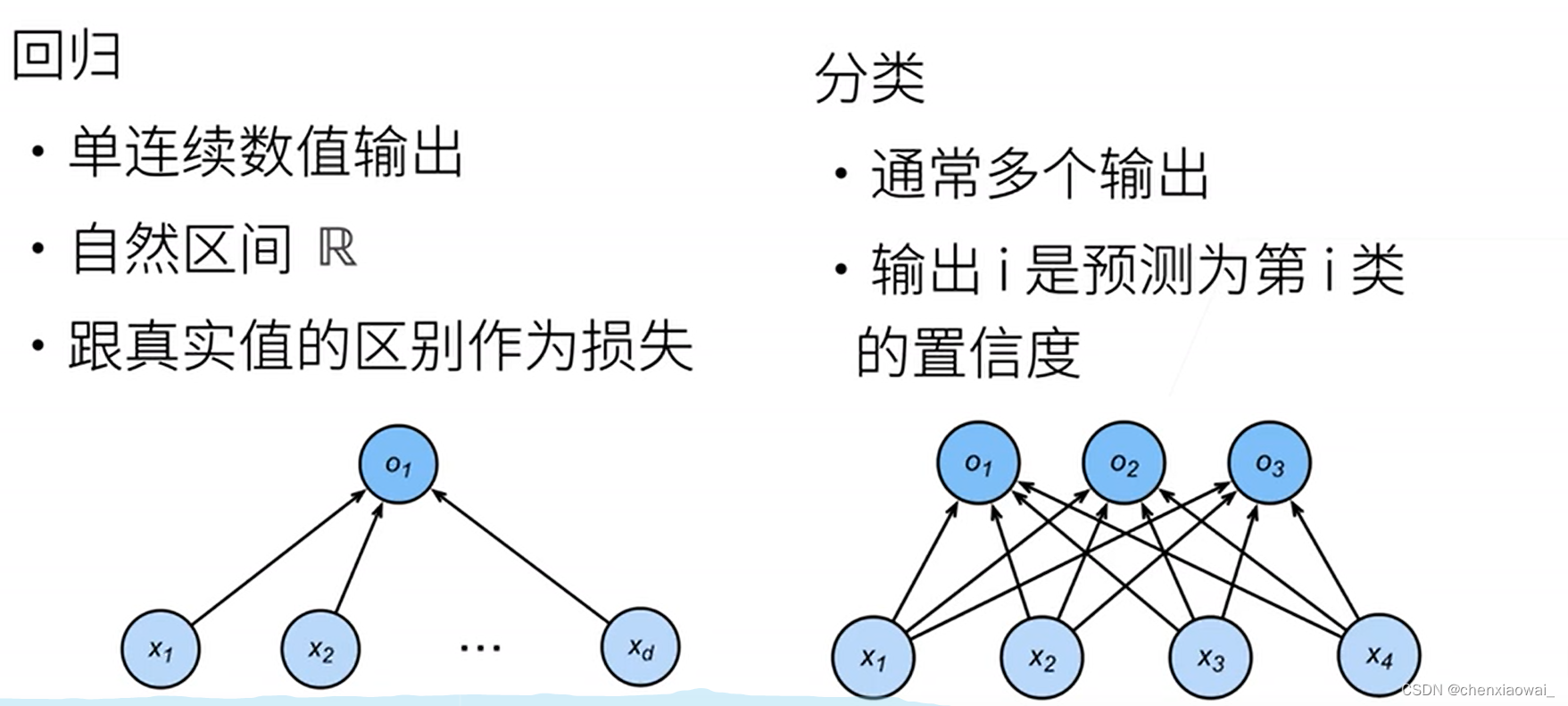
- 回归vs分类(从回归到多类分类)
回归估计一个连续值;分类预测一个离散类别。
- 从回归到多类分类 — 均方损失
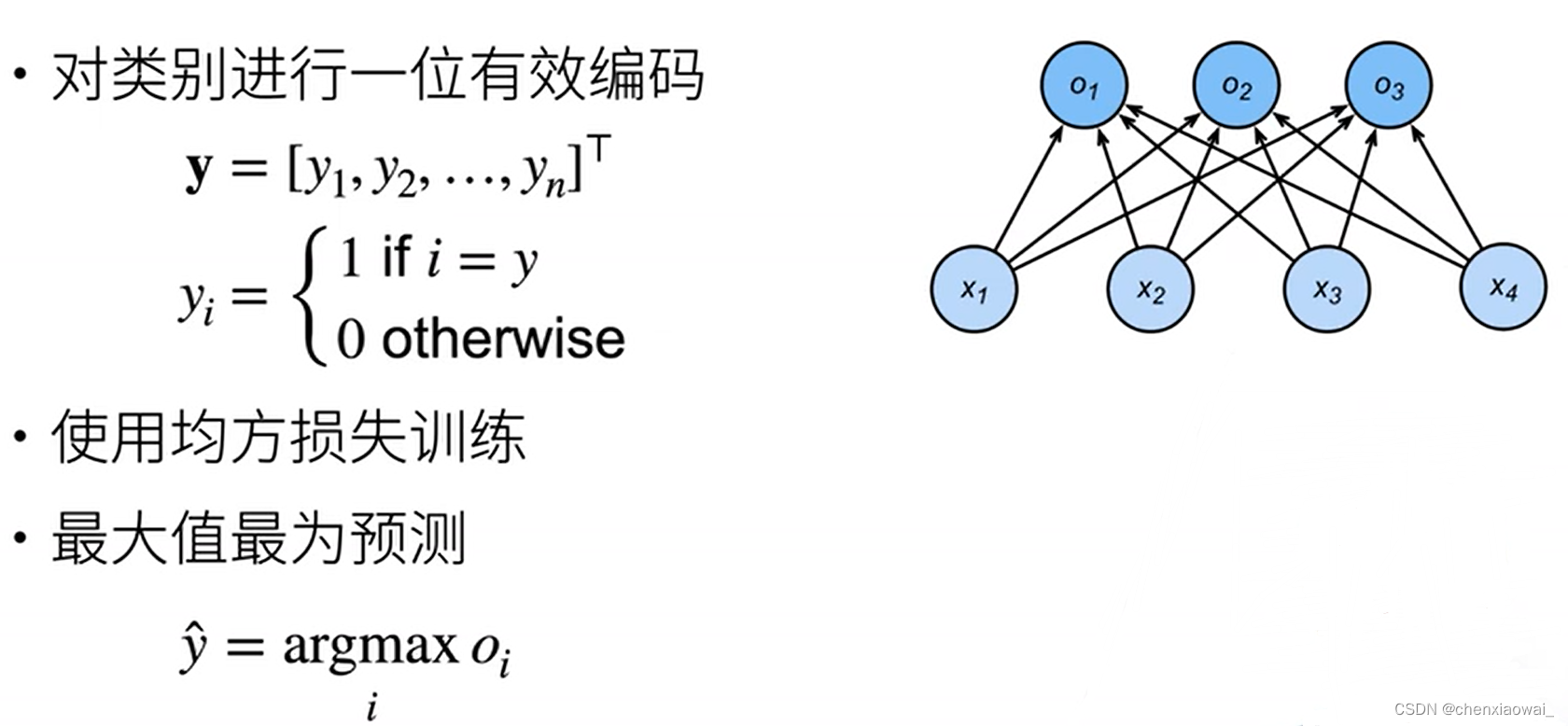
- 从回归到多类分类 — 无校验比例
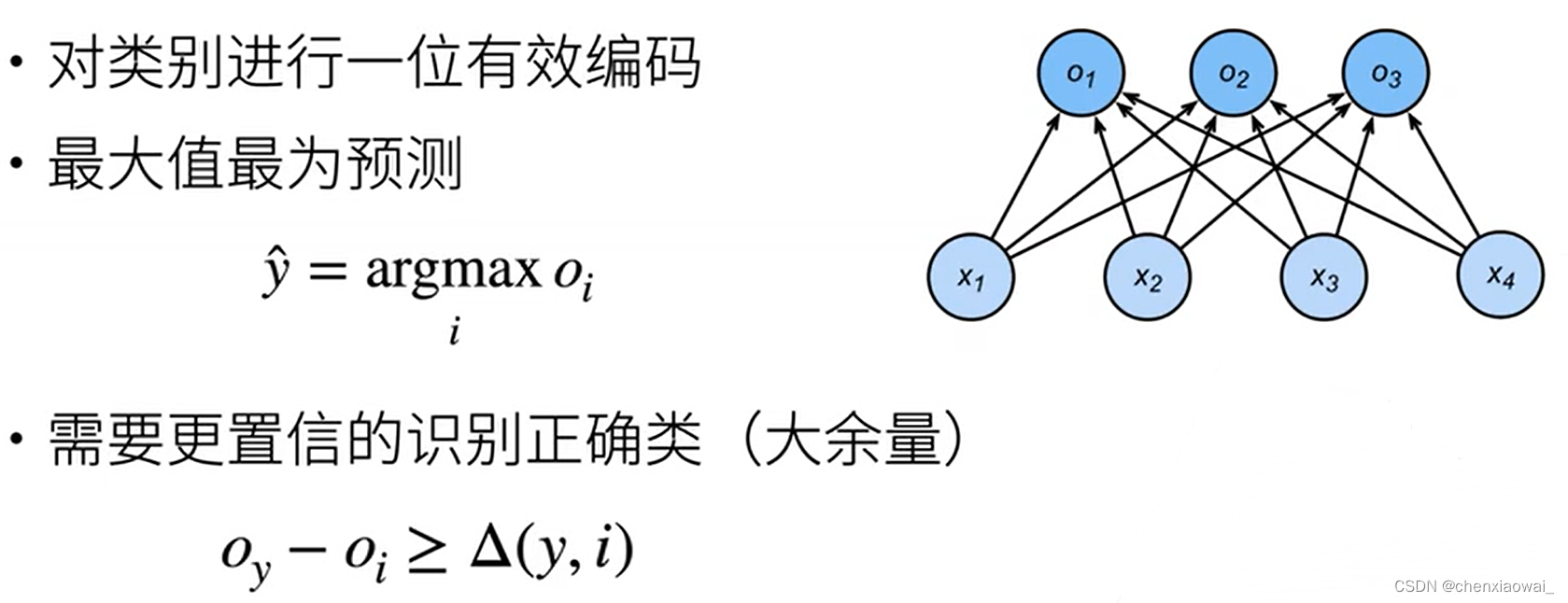
- 从回归到多类分类 — 校验比例
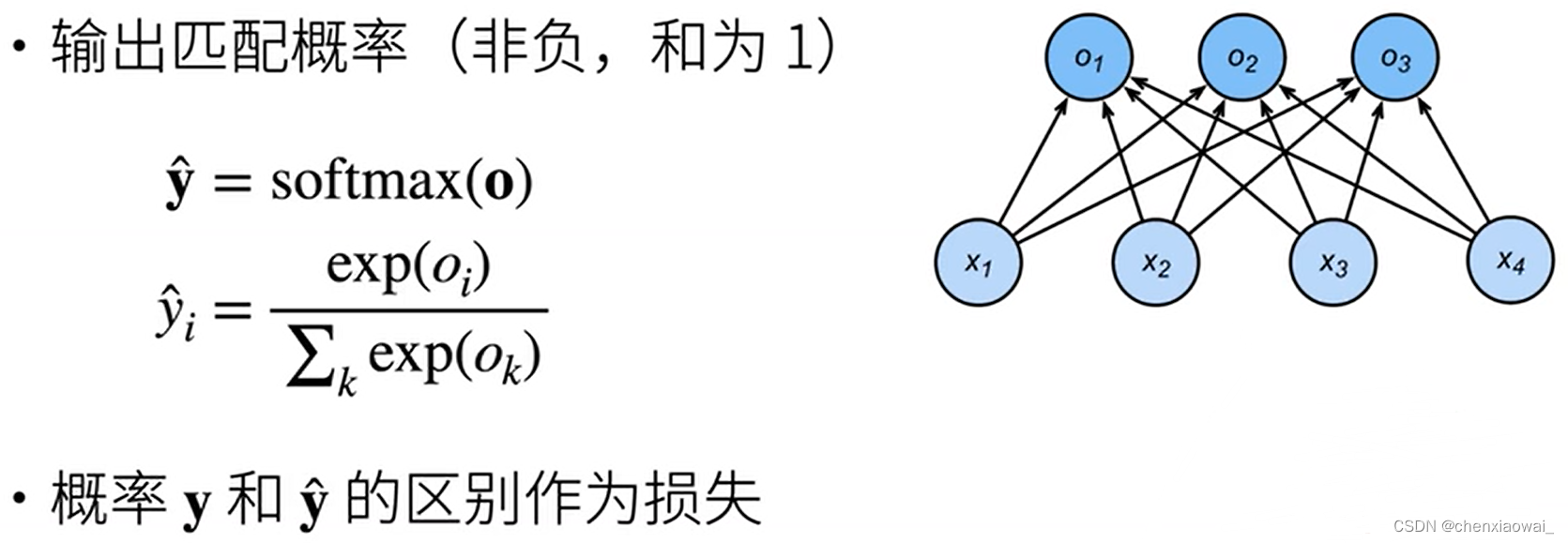
- Softmax和交叉熵损失

- 总结

损失函数
本节代码文件在源代码文件的chapter_linear-networks/softmax-regression.ipynb中
损失函数用来衡量预测值与真实值之间的区别,是机器学习里非常重要的概念。下面介绍三种常用的损失函数。
- ①L2 Loss
l ( y , y ′ ) = ∣ y − y ′ ∣ \it l(y,y') = \mid y-y' \mid l(y,y′)=∣y−y′∣
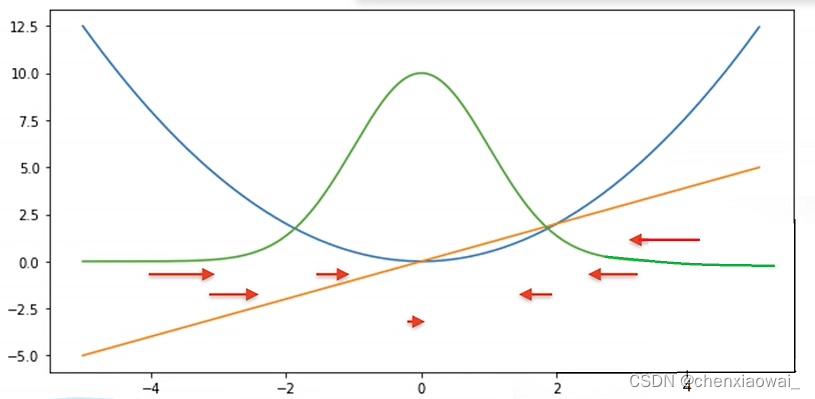
蓝色曲线:表示当y=0时,变换预测值y’。
绿色曲线:表示似然函数。
橙色曲线:表示损失函数的梯度,可以发现,当y与y’相差较大的时候,梯度的绝对值也较大。
- ②L1 Loss
l ( y , y ′ ) = 1 2 ( y − y ′ ) 2 \it l(y,y') = \frac{1}{2} ( y-y')^2 l(y,y′)=21(y−y′)2
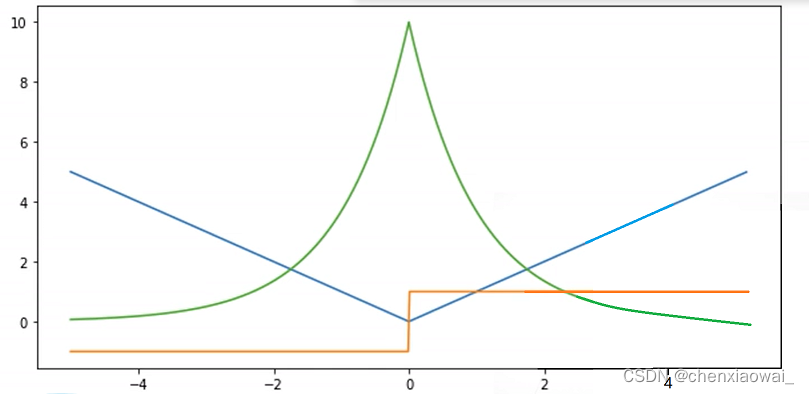
蓝色曲线:表示当y=0时,变换预测值y’。
绿色曲线:表示似然函数。
橙色曲线:表示损失函数的梯度,可以发现,当y’>0时,导数为1,当y’
- ①L2 Loss
- 回归vs分类(从回归到多类分类)
- 实现流程
- 实现流程
- 梯度下降
- 线性模型
- 正向累积与反向累积复杂度比较
- 向量链式法则
-
- 张量的按元素操作
- reshape函数
- 创建数组
- 优化算法









