本文力求做到系统、准确、简洁、易懂的讲解蒙特卡洛搜索树算法,为此参考了大量资料和文章。
(图片来源网络,侵删)
前言
人工智能Alphago,成为最顶尖的围棋大师,不由得让人产生探索它背后的算法的兴趣。
在搜索空间巨大的围棋问题中,Alphago是通过什么算法能在较短的时间搜索每一个局面的(近似)最优解?

(图片来源网络,侵删)
Alphago使用的算法如下:
蒙特卡洛树搜索的适用范围
蒙特卡洛树搜索算法本质上是一种启发式搜索算法。
通过蒙特卡洛方法设计出较为准确的估价函数,使得问题在仅需迭代较少的次数就能得出(近似)最优解。
通常,在博弈问题中可以采用蒙特卡洛数搜索。
对于以下情况特别适用:
- 搜索空间特别大。
- 难以采用传统方法(如:dp,贪心)直接设计出特别通用的估价函数(比如围棋)。
蒙特卡洛树搜索的作用
要先明确算法有什么作用:
蒙特卡洛树算法用于求当前局面如何决策是最优的。
在围棋中,每次再对手走完一步新局面产生的时候,都要重新运行蒙特卡洛树算法找出面对当前局面自己的最优解。
算法流程
前置:蒙特卡洛方法
用途:评估当前局面选取哪个决策最优
以围棋为例,难以直接用传统的dp,贪心等方法设计出估价函数。
这时可以采用蒙特卡洛方法:
对于每个局面,随机轮流走棋,直到最后定出胜负。
在随机走大量次数的时候,取获胜次数最多的。
这时一个正确性难以保证的伪算法:
对于某个局面的某步决策,如果对方有几乎所有情况都将处于劣势,但是只要有一种情况必胜,那么这样的决策是绝对不可能采取的。
但是直接采用上面的蒙特卡洛方法恰恰容易采取这样的决策,因为这种决策胜率特别高。
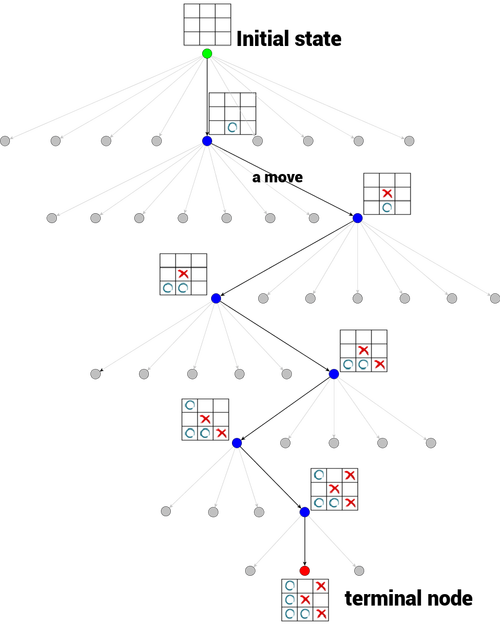
流程
算法的设计思路:
类似人的下棋思维,在考虑









