【博弈论】第二讲：纳什均衡的混合战略（有限数量战略）

纳什均衡的混合战略

• 混合战略概念
• 混合战略的期望收益求解
• 【例题】
• • 有一种求纳什均衡的办法是：我们要求支付最大化
  • 还有一种方法是支付等值法：
  • 第三种方法是反应曲线法（如何应对是最佳反应）
  • 求混合战略均衡要先剔除劣战略：
  • 【例题】【广告决策】
  • 【例题】
  • 【例题】
  • 【税收检查】
  • 【例题】【小偷与守卫】
  • 【例题】（考试题）
  • 【例题】试用支付最大化法、支付等值法、反应曲线法,求下列矩阵表示的完全相信静态博弈的纳什均衡。
  • 【例题】求职博弈
  • 【例题】支撑求解法求混合战略纳什均衡

    

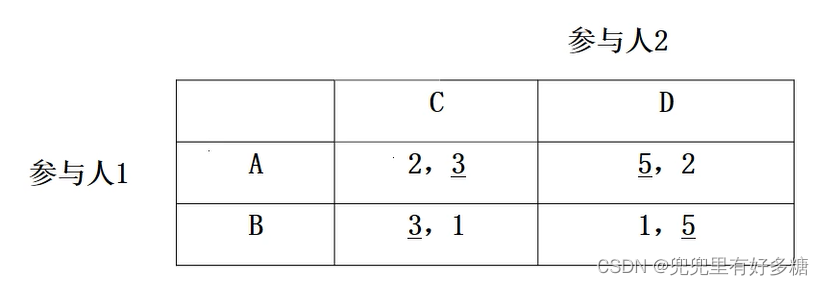
    1. 原则一:战略的保密性与随机性
    2. 原则二:不能给对方以可乘之机（对方选择A和B，或者C和D的收益没有差别，就是不给对方可乘之机）

    混合战略概念

    在 n n n个参与人的博弈 G = { S 1 ， . . . ， S n ; u 1 ， . . . ， u n } G=\left\{S_1，...，S_n; u_1，...，u_n\right\} G={S1​，...，Sn​;u1​，...，un​}中，参与人 i i i的战略空间为 S , = { S 1 … , S i } S_,= \left\{S_1…, S_i\right\} S,​={S1​…,Si​}，则参与人i以概率分布 p i = ( p i 1 , … , p i x ) p_i=(p_{i1},…,p_{ix}) pi​=(pi1​,…,pix​)随机选择其 k k k个可选战略称为一个“混合战略”，其中 0 ≤ p i k ≤ 1 0≤p_{ik}≤1 0≤pik​≤1且 p i 1 + … + p i k = 1 p_{i1}+…+p_{ik}=1 pi1​+…+pik​=1。

    • 纯战略(pure strategies):如果一个战略规定参与人在一个给定的信息情况下只选择一种特定的行动。
    • 混合战略(mixed strategies):如果一个战略规定参与人在给定的信息情况下，以某种概率分布随机地选择不同的行动。
    • 在静态博弈里，纯战略等价于特定行动，混合战略是不同行动之间的随机选择。

      混合战略的期望收益求解

      与混合战略(mixed strategies)相伴随的一个问题,是参与人支付的不确定(uncertainty)。可用期望支付(expected payoff)来描述:有n个可能的取值X,Xg…,Xn，并且这些取值发生的概率分别为p,P2.…., pn，那么可以将这个数量指标的期望值定义为发生概率作为权重的所有可能取值的加权平均，也就是

      E U A = p 1 x 1 + p 2 x 2 + … + p n x n E U_A=p_1 x_1+p_2 x_2+\ldots+p_n x_n EUA​=p1​x1​+p2​x2​+…+pn​xn​

      【例题】

      政府和流浪汉的博弈

      政府想帮助流浪汉,但前提是后者必须试图寻找工作，否则不予帮助;而流浪汉若知道政府采用救济战略的话，他就不会寻找工作。他们只有在得不到政府救济时才会寻找工作。他们获得的支付如图所示:

      

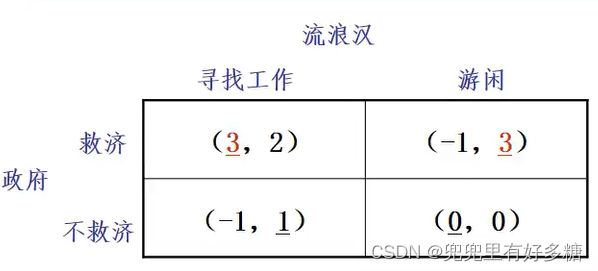
      通过观察划线法可以得知：没有一个双划线的得益数组，也就是没有一个纯战略纳什均衡，也就是政府没有一个最好的选择，流浪汉也没有一个最好的选择。

      在这样一种情况下我们仍然要确定各自的一个行为选择的时候我们就采用混合战略方式。

      假定政府采用混合战略：选择救济的概率是 θ \theta θ，不救济的概率是 1 − θ 1-\theta 1−θ。

      流浪汉的混合战略是：选择找工作的概率： γ \gamma γ，游闲的概率： 1 − γ 1-\gamma 1−γ

      δ G = ( θ , 1 − θ ) δ L = ( γ , 1 − γ ) \delta_G=(\theta, 1-\theta) \quad \delta_L=(\gamma, 1-\gamma) δG​=(θ,1−θ)δL​=(γ,1−γ)

      

      有一种求纳什均衡的办法是：我们要求支付最大化

      政府的期望效用函数是：

      v G ( δ G , δ L ) = θ [ 3 γ + ( − 1 ) ( 1 − γ ) ] + ( 1 − θ ) [ − γ + 0 ( 1 − γ ) ] = θ ( 5 γ − 1 ) − γ v_G\left(\delta_G, \delta_L\right)=\theta[3 \gamma+(-1)(1-\gamma)]+(1-\theta)[-\gamma+0(1-\gamma)]=\theta(5 \gamma-1)-\gamma vG​(δG​,δL​)=θ[3γ+(−1)(1−γ)]+(1−θ)[−γ+0(1−γ)]=θ(5γ−1)−γ

      政府最优化的一阶条件为： ∂ v G ∂ θ = 5 γ − 1 = 0 ⇒ γ ∗ = 0.2 \frac{\partial v_G}{\partial \theta}=5 \gamma-1=0 \Rightarrow \gamma^*=0.2 ∂θ∂vG​​=5γ−1=0⇒γ∗=0.2

      流浪汉的期望效用函数为：

      v L ( δ G , δ L ) = γ [ 2 θ + 1 ( 1 − θ ) ] + ( 1 − γ ) [ 3 θ + 0 ( 1 − θ ) ] = − γ ( 2 θ − 1 ) + 3 θ v_L\left(\delta_G, \delta_L\right)=\gamma[2 \theta+1(1-\theta)]+(1-\gamma)[3 \theta+0(1-\theta)]=-\gamma(2 \theta-1)+3 \theta vL​(δG​,δL​)=γ[2θ+1(1−θ)]+(1−γ)[3θ+0(1−θ)]=−γ(2θ−1)+3θ

      流浪汉最优化的一阶条件为： ∂ v L ∂ γ = − ( 2 θ − 1 ) = 0 ⇒ θ ∗ = 0.5 \frac{\partial v_L}{\partial \gamma}=-(2 \theta-1)=0 \Rightarrow \theta^*=0.5 ∂γ∂vL​​=−(2θ−1)=0⇒θ∗=0.5

      上面这种求导来求最大值的算法其实有点不符合数学的逻辑，另一个问题是我们求政府的支付最大化求出的却是 γ \gamma γ的最大值，求流浪汉的最大支付函数求出的却是 θ \theta θ，都是相反的。所以这一点也比较反常识一点。

      还有一种方法是支付等值法：

      就是完全利用我们一开始提到的原则：

      找不到纯战略的情况下，就选择让对方无机可乘。也就是参与人一选择某个方案，会让参与人二选择A方案与选择B方案的收益是无差异的。就称之为等值法。

      • 如果政府选择救济策略： θ = 1 \theta=1 θ=1，那么他这时候的期望收益是：

        v G ( 1 , γ ) = 3 γ + ( − 1 ) ( 1 − γ ) = 4 γ − 1 \begin{aligned} & v_G(1, \gamma)=3 \gamma+(-1)(1-\gamma) \\ & =4 \gamma-1 \end{aligned} ​vG​(1,γ)=3γ+(−1)(1−γ)=4γ−1​

      • 政府如果选择不救济策略： θ = 0 \theta=0 θ=0，这时候政府的期望效用是

        v G ( 0 , γ ) = − 1 γ + 0 ( 1 − γ ) = − γ \begin{aligned} & v_G(0, \gamma)=-1 \gamma+0(1-\gamma) \\ & =-\gamma \end{aligned} ​vG​(0,γ)=−1γ+0(1−γ)=−γ​

        如果一个混合战略是流浪汉的最优选择，那一定意味着政府在救济与不救济之间是无差异的，即:

        v G ( 1 , γ ) = 4 γ − 1 = − γ = v G ( 0 , γ ) ⇒ γ ∗ = 0.2 \begin{aligned} & v_G(1, \gamma)=4 \gamma-1=-\gamma=v_G(0, \gamma) \\ & \Rightarrow \gamma^*=0.2 \end{aligned} ​vG​(1,γ)=4γ−1=−γ=vG​(0,γ)⇒γ∗=0.2​

        可以看出与求导数方法算出的结果是一样的。

        同理：如果一个混合战略是政府的最优选择，那一定意味着流浪汉在寻找工作与游闲之间是无差异的，即:

        v L ( 1 , θ ) = 1 + θ = 3 θ = v L ( 0 , θ ) ⇒ θ ∗ = 0.5 \begin{aligned} & v_L(1, \theta)=1+\theta=3 \theta=v_L(0, \theta) \\ & \Rightarrow \theta^*=0.5 \end{aligned} ​vL​(1,θ)=1+θ=3θ=vL​(0,θ)⇒θ∗=0.5​

      • 如果政府救济的概率小于0.5;则流浪汉的最优选择是寻找工作

      • 如果政府救济的概率大于0.5; 则流浪汉的最优选择是游闲等待救济

      • 如果政府救济的概率正好等于0.5;流浪汉的选择无差异

        第三种方法是反应曲线法（如何应对是最佳反应）

        【例】假设甲、乙均采用混和战略,随机地以 p p p的概率出红牌和以 ( 1 − p ) (1-p) (1−p)的概率出黑牌,而乙则随机地以 q q q的概率出红牌和以 ( 1 − q ) (1-q) (1−q)的概率出黑牌。

        

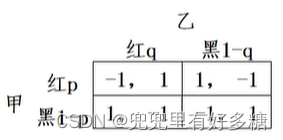
        先把每个人的总期望收益写出来。

        • 甲的期望支付是：

          U A ( p , q ) = ( − 1 ) [ p q + ( 1 − p ) ( 1 − q ) ] + 1 [ p ( 1 − q ) + ( 1 − p ) q ] = 2 p ( 1 − 2 q ) + ( 2 q − 1 ) U_A(p, q)=(-1)[p q+(1-p)(1-q)]+1[p(1-q)+(1-p) q]=2 p(1-2 q)+(2 q-1) UA​(p,q)=(−1)[pq+(1−p)(1−q)]+1[p(1−q)+(1−p)q]=2p(1−2q)+(2q−1)

          （最后整理成一部分和 p p p有关的，一部分和 p p p无关的）

        • 乙的期望支付是：

          U B ( p , q ) = 1 [ p q + ( 1 − p ) ( 1 − q ) ] + ( − 1 ) [ p ( 1 − q ) + ( 1 − p ) q ] = 2 q ( 1 − 2 p ) + ( 2 p − 1 ) U_B(p, q)=1[p q+(1-p)(1-q)]+(-1)[p(1-q)+(1-p) q]=2 q(1-2 p)+(2 p-1) UB​(p,q)=1[pq+(1−p)(1−q)]+(−1)[p(1−q)+(1−p)q]=2q(1−2p)+(2p−1)

          （最后整理成一部分和 q q q有关的，一部分和 q q q无关的）

          A A A的目标是期望支付越大越好。之所以把 A A A的期望支付整理成不含 p p p的一项和含 p p p的一项，是因为 A A A只能选择 p p p而不能 q q q，因此， A A A能通过选择 p p p来影响第一项，而不能直接影响第二项。 ( 1 − 2 q ) > 0 (1-2q)>0 (1−2q)>0即 q 1 / 2 \\ {[0,1],} & \text { 如果 } \mathrm{q}=1 / 2 \\ 1 & \text { 如果 } \mathrm{q}1/2 如果 q=1/2 如果 q 1 / 2 [ 0 , 1 ] ,  如果  p = 1 / 2 0  如果  p 1 / 2 \\ {[0,1],} & \text { 如果 } \mathrm{p}=1 / 2 \\ 0 & \text { 如果 } \mathrm{p}1/2 如果 p=1/2 如果 p