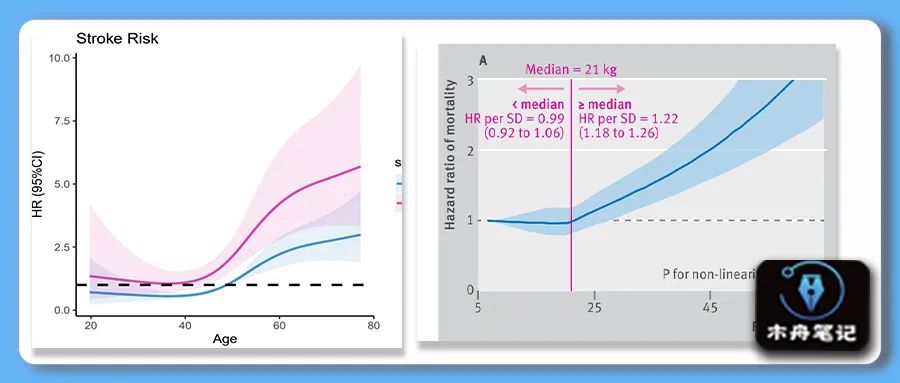
在科学研究中,我们经常构建回归模型来分析自变量和因变量之间的关系。大多数的回归模型有一个重要的假设就是自变量和因变量呈线性关联。当自变量和因变量之间为非线性关系时,可以将连续型变量转化为分类变量,但是分类变量的类别数目以及节点位置的选择一般会带有主观性并且分类变量会损失部分信息;也可以直接拟合自变量和因变量之间的非线性关系,但是直接构建多项式回归可能存在过度拟合、共线性等问题。因此,一个更好的解决方法是拟合自变量与因变量之间的非线性关系,「限制性立方样条」(Restricted cubic spline,RCS)就是分析非线性关系的最常见的方法之一。
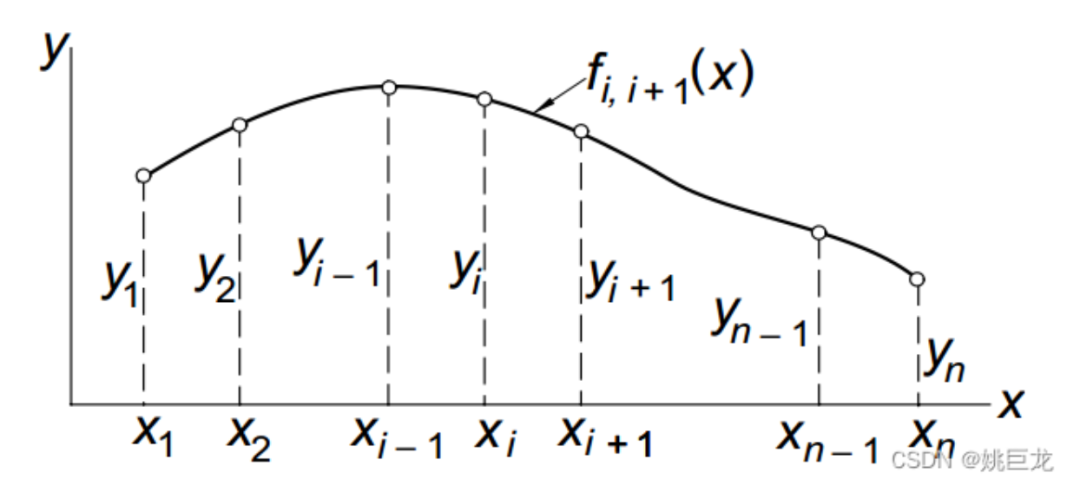
样条(spline)原本是指是一种灵活的细木条或金属条,用来绘制平滑曲线。样条曲线本质是一个分段多项式函数,此函数受限于某些控制点,称为 “节点”,节点放置在数据范围内的多个位置,多项式的类型以及节点的数量和位置决定了样条曲线的类型。立方则指的是 函数为3次多项式。限制是在回归样条的基础上附加要求:样条函数在自变量数据范围两端的两个区间 [X1,X2) 和 (Xn-1,Xn] 内是线性函数。
 RCS曲线
RCS曲线
RCS节点的数量比位置更重要。由于节点个数的选择和自由度有关, 所以当样本量比较大的时候可以取较多的节点。但是节点越多, 自由度越大, 模型越复杂, 越难解在「«Regression Modeling Strategies»」这本书中,Harrell 建议节点数为4时,模型的拟合效果较好,即同时可以兼顾曲线的平滑程度以及避免过拟合造成的精确度降低。当样本量较大时,5个节点是更好的选择。小样本(n









