
个人简介:
> 📦个人主页:赵四司机
> 🏆学习方向:JAVA后端开发
> ⏰往期文章:SpringBoot项目整合微信支付
> 🔔博主推荐网站:牛客网 刷题|面试|找工作神器
> 📣种一棵树最好的时间是十年前,其次是现在!
> 💖喜欢的话麻烦点点关注喔,你们的支持是我的最大动力。
前言:
通过这篇文章你将了解卷积理论与频域的联系,并且你还将学会频域增强的两个常用方法——低通滤波和高通滤波。
目录
一:实验原理
二:低通滤波
三:高通滤波
四:代码实战
1.实验内容
2.Butterworth低通滤波器
3.Butterworth高通滤波器
4.实验分析
一:实验原理
卷积理论是频域技术的基础。设函数f(x,y)与线性位不变算子h(x,y)的卷积结果是g(x,y),即
g(x,y)=h(x,y)*f(x,y)
那么,根据卷积定理在频域有
G(u,v)=H(u,v)F(u,v)
其中,G(u,v)、H(u,v)、F(u,v)分别是 g(x,y)、h(x,y)、f(x,y)的傅立叶变换。频域增强的主要步骤是:
- 计算所需增强图的傅立叶变换;
- 将其与一个(根据需要设计的)转移函数相乘;
- 在将结果进行傅立叶反变换以得到增强的图。
常用的频域增强方法有低通滤波和高通滤波。下面分别介绍这两种滤波方法。
二:低通滤波
图像的能量大部分集中在幅度谱的低频和中频部分,而图像的边缘和噪声对应于高频部分。因此能降低高频成分幅度的滤波器就能减弱噪声的影响。
Butterworth低通滤波器是一种物理上可以实现的低通滤波器。n阶截断频率为d0的Butterworth低通滤波器的转移函数为:
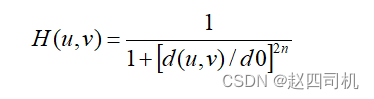
% 实现Butterworth低通滤波器
I1=imread('lena.png');
I2=imnoise(I1,'salt');
f=double(I2);
g=fft2(f); %采用傅立叶变换
g=fftshift(g); %数据矩阵平移
[N1,N2]=size(g);
n=2;
d0=50;
d1=5;
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
%计算Butterworth低通变换函数
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
X2=ifft2(result);
X3=uint8(real(X2));
三:高通滤波
高通滤波也称高频滤波,它的频率值在0频率处为单位1,随着频率的增长,传递函数的值逐渐增加;当频率增加到一定值后,传递函数的值通常又回到0值或者降低到某个大于1的值。在前一种情况下,高频增强滤波器实际上是一种带通滤波器,只不过规定0频率处的增益为单位1。
在实际应用中,为了减少图像中面积大而且缓慢变化的成分的对比度,有时让0频率处的增益小于单位1更合适。如果传递函数通过原点,则可称为laplacian滤波器。
% 实现Butterworth高通滤波器参考代码
%计算Butterworth高通变换函数
if d==0
h=0;
else
h=1/(1+(d1/d)^(2*n));
end
result(i,j)=h*g(i,j);
result=ifftshift(result);
X4=ifft2(result);
X5=uint8(real(X2));
figure(1),subplot(2,2,1),imshow(I1),title('原图像');
subplot(2,2,2),imshow(I2),title('加噪图像');
subplot(2,2,3),imshow(X3),
title('Butterworth低通滤波器去噪图像');
subplot(2,2,4),imshow(X5),
title('Butterworth高通滤波器去噪图像');
四:代码实战
1.实验内容
分别用两张以上不同的图片,实现Butterworth低通滤波器和Butterworth高通滤波器, 分别加入不同噪声如高斯噪声,椒盐噪声 (可选加入:指数分布噪声,泊松噪声,乘性噪声),分析Butterworth高通和低通的滤波效果。分析比较Butterworth低通滤波器和不同空域平滑滤波器的差别,结合实验结果对比图进行分析。
2.Butterworth低通滤波器
function I = Butterworth_low(I_in)
f=double(I_in);
g=fft2(f); %采用傅立叶变换
g=fftshift(g); %数据矩阵平移
[N1,N2]=size(g);
result=zeros(N1,N2);
n=2;
d0=50;
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
%计算Butterworth低通变换函数
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
X2=ifft2(result);
I=uint8(real(X2));
end
%lena图片
X1_1=Butterworth_low(I1_1);
figure,subplot(131),imshow(I1),title('lena原图像');
subplot(132),imshow(I1_1),title('加入高斯噪声');
subplot(133),imshow(X1_1),title('Butterworth低通滤波');

图2.1-1 lena图像加入高斯噪声的低通滤波结果
X1_2=Butterworth_low(I1_2);
figure,subplot(131),imshow(I1),title('lena原图像');
subplot(132),imshow(I1_2),title('加入椒盐噪声');
subplot(133),imshow(X1_2),title('Butterworth低通滤波');

图2.1-2 lena图像加入椒盐噪声的低通滤波结果
X1_3=Butterworth_low(I1_3);
figure,subplot(131),imshow(I1),title('lena原图像');
subplot(132),imshow(I1_3),title('加入泊松噪声');
subplot(133),imshow(X1_3),title('Butterworth低通滤波');

图2.1-3 lena图像加入泊松噪声的低通滤波结果
%pout图片
X2_1=Butterworth_low(I2_1);
figure,subplot(131),imshow(I2),title('pout原图像');
subplot(132),imshow(I2_1),title('加入高斯噪声');
subplot(133),imshow(X2_1),title('Butterworth低通滤波');

图2.1-4 pout图像加入高斯噪声的低通滤波结果
X2_2=Butterworth_low(I2_2);
figure,subplot(131),imshow(I2),title('pout原图像');
subplot(132),imshow(I2_2),title('加入椒盐噪声');
subplot(133),imshow(X2_2),title('Butterworth低通滤波');

图2.1-5 pout图像加入椒盐噪声的低通滤波结果
X2_3=Butterworth_low(I2_3);
figure,subplot(131),imshow(I2),title('pout原图像');
subplot(132),imshow(I2_3),title('加入泊松噪声');
subplot(133),imshow(X2_3),title('Butterworth低通滤波');

图2.1-6 pout图像加入泊松噪声的低通滤波结果
%自定义scenery图像 X3_1=Butterworth_low(I3_1); figure,subplot(131),imshow(I3),title('scenery原图像'); subplot(132),imshow(I3_1),title('加入高斯噪声'); subplot(133),imshow(X3_1),title('Butterworth低通滤波');

图2.1-7 scenery图像加入高斯噪声的低通滤波结果
X3_2=Butterworth_low(I3_2);
figure,subplot(131),imshow(I3),title('scenery原图像');
subplot(132),imshow(I3_2),title('加入椒盐噪声');
subplot(133),imshow(X3_2),title('Butterworth低通滤波');

图2.1-8 scenery图像加入椒盐噪声的低通滤波结果
X3_3=Butterworth_low(I3_3);
figure,subplot(131),imshow(I3),title('scenery原图像');
subplot(132),imshow(I3_3),title('加入泊松噪声');
subplot(133),imshow(X3_3),title('Butterworth低通滤波');

图2.1-9 scenery图像加入泊松噪声的低通滤波结果
3.Butterworth高通滤波器
function I = Butterworth_high(I_in) f=double(I_in); g=fft2(f); %采用傅立叶变换 g=fftshift(g); %数据矩阵平移 [N1,N2]=size(g); result=zeros(N1,N2); n=2; d1=5; n1=fix(N1/2); n2=fix(N2/2); for i=1:N1 for j=1:N2 d=sqrt((i-n1)^2+(j-n2)^2); %计算Butterworth低通变换函数 if d==0 h=0; else h=1/(1+(d1/d)^(2*n)); end result(i,j)=h*g(i,j); end end result=ifftshift(result); X2=ifft2(result); I=uint8(real(X2)); end

图2.2-1 lena图像加入高斯噪声的高通滤波结果

图2.2-2 lena图像加入椒盐噪声的高通滤波结果

图2.2-3 lena图像加入泊松噪声的高通滤波结果

图2.2-4 pout图像加入高斯噪声的高通滤波结果

图2.2-5 pout图像加入椒盐噪声的高通滤波结果

图2.2-6 pout图像加入泊松噪声的高通滤波结果

图2.2-7 scenery图像加入高斯噪声的高通滤波结果

图2.2-8 scenery图像加入椒盐噪声的高通滤波结果

图2.2-9 scenery图像加入泊松噪声的高通滤波结果
注:为了便于调用,我将低通高通滤波封装成了函数的形式,然后再对不同的图片进行函数调用;为了节省篇幅,这里仅将主要代码放上来,且不再将Butterworth高通滤波的调用代码放上来。
4.实验分析
图像增强可以分为空间域、频率域和彩色增强,其包含的内容如下图所示:
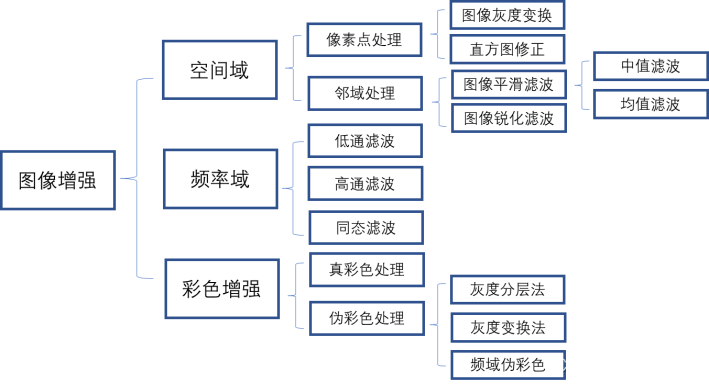
低通高通滤波是在频率域上对图像的增强,而中值滤波、均值滤波等则是在空间域上对图像的增强。
一开始我的理解为对于二值图像,当某一像素点与中心点的距离大于D0时,该点的像素值就会被置0,因为根据理想低通滤波函数当D>D0时H=0,当D









