关联网站:

einops官网
torch.einsum( equation , * operands ) → Tensor
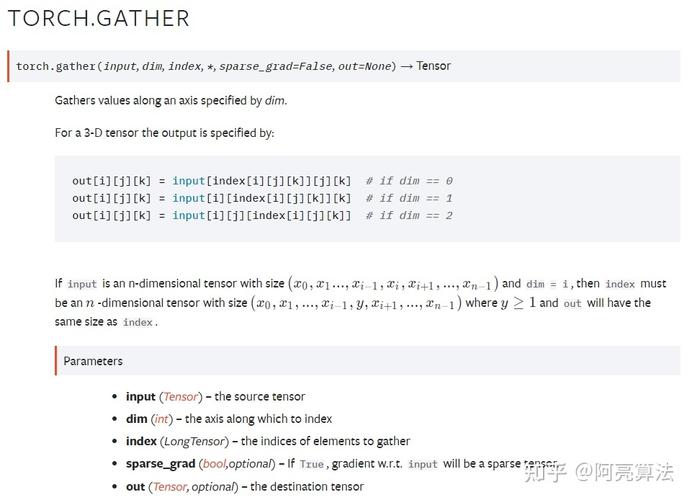
对输入元素operands沿指定的维度、使用爱因斯坦求和符号的乘积求和。
参数:
-
equation ( string ) – 爱因斯坦求和的下标。
-
operands(List [ Tensor ])——计算爱因斯坦求和的张量。
Einsum允许计算许多常见的多维线性代数数组运算,方法是根据由equation给出的爱因斯坦求和约定,以速记(short-hand)格式表示它们。这种格式的细节在下面描述,但通常想法是operands 用一些下标标记输入的每个维度,并定义哪些下标是输出的一部分,operands然后通过对下标不属于输出维度的元素的乘积求和来计算输出。例如,矩阵乘法可以使用einsum计算为torch.einsum(“ij,jk->ik”, A, B)。这里,j 是求和下标,i 和 k 是输出下标(有关原因的更多详细信息,请参见下面的部分)。
equation 参数说明:
equation字符串以与维度相同的顺序指定输入的每个维度的下标( [a-z,A-Z] operands中的字母) ,用逗号 (‘,’) 分隔每个操作数的下标,例如’ij,jk’指定两个二维操作数的下标。标有相同下标的维度必须是可广播的,即它们的大小必须匹配或为1。例外情况是,如果对相同的输入操作数重复下标,在这种情况下,此操作数的标有此下标的维度必须在大小上匹配,并且操作数将被其沿这些维度的对角线替换。equation中只出现一次的下标将是输出的一部分,按字母顺序递增排序。输出是通过按元素乘以输入来计算的operands,它们的维度根据下标对齐,然后对下标不属于输出的维度求和。
或者,可以通过在等式末尾添加箭头 (->) 后跟输出下标来显式定义输出下标。例如,以下等式计算矩阵乘法的转置:‘ij,jk->ki’。对于某些输入操作数,输出下标必须至少出现一次,而对于输出则最多出现一次。
可以使用省略号 (...) 代替下标来广播省略号所涵盖的维度。每个输入操作数最多可以包含一个省略号,它将覆盖下标未覆盖的维度,例如,对于具有 5 维的输入操作数,等式“ab…c”中的省略号覆盖第三和第四维。省略号不需要覆盖operands中相同数量的维度,但省略号的“形状”(它们覆盖的维度的大小)必须一起传播。如果未使用箭头 (->) 表示法显式定义输出,则省略号将首先出现在输出(最左侧的维度)中,位于输入操作数仅出现一次的下标标签之前。例如下面的等式实现批量矩阵乘法’…ij,…jk’。
最后几点注意事项:equation可能在不同元素(下标、省略号、箭头和逗号)之间包含空格,但类似“…”的内容无效。空字符串 ’ ’ 对标量operands有效。
注:
- torch.einsum处理省略号 (‘…’) 的方式与 NumPy 不同,因为它允许对省略号覆盖的维度求和,也就是说,省略号不需要是输出的一部分。
- 此函数不会优化给定的表达式,因此用于相同计算的不同公式可能会运行得更快或消耗更少的内存。像 opt_einsum ( https://optimized-einsum.readthedocs.io/en/stable/
)这样的项目可以为你优化公式。
- 从 PyTorch 1.10 开始,还支持子列表格式(请参见下面的示例)。在这种格式中,每个操作数的下标由子列表指定,子列表是 [0, 52) 范围内的整数列表。这些子列表跟在它们的操作数之后,一个额外的子列表可以出现在输入的末尾以指定输出的下标。例如torch。einsum
(op1, sublist1, op2, sublist2, …, [subslist_out])。可以在子列表中提供Python
的Ellipsis对象,以启用广播,如上面的方程式部分所述。torch.einsum()
例:
# trace(迹) >>> torch.einsum('ii', torch.randn(4, 4)) tensor(-1.4157) # diagonal(对角线) >>> torch.einsum('ii->i', torch.randn(4, 4)) tensor([ 0.0266, 2.4750, -1.0881, -1.3075]) # outer product(外积) >>> x = torch.randn(5) tensor([-0.3550, -0.6059, -1.3375, -1.5649, 0.2675]) >>> y = torch.randn(4) tensor([-0.2202, -1.5290, -2.0062, 0.9600]) >>> torch.einsum('i,j->ij', x, y) tensor([[ 0.0782, 0.5428, 0.7122, -0.3408], [ 0.1334, 0.9264, 1.2156, -0.5817], [ 0.2945, 2.0451, 2.6834, -1.2840], [ 0.3445, 2.3927, 3.1396, -1.5023], [-0.0589, -0.4089, -0.5366, 0.2568]]) # batch matrix multiplication(批量矩阵乘法) >>> As = torch.randn(3,2,5) tensor([[[-0.0306, 0.8251, 0.0157, -0.4563, 0.5550], [-1.4550, 0.0762, 0.9258, 0.1198, -1.1737]], [[-0.4460, -0.7224, 0.7260, 0.7552, 0.0326], [-0.3904, -1.2392, 0.4848, -0.4756, 0.2301]], [[ 1.5307, 0.7668, -1.9426, 1.7473, -0.6258], [ 0.6758, 1.8240, -0.2053, 0.0973, -0.6118]]]) >>> Bs = torch.randn(3,5,4) tensor([[[-0.7054, -0.2155, -1.5458, -0.8236], [-1.4957, -2.2604, 0.6897, -1.0360], [ 1.2924, 0.2798, 1.0544, 0.3656], [-0.3993, -1.2463, -0.6601, 0.2706], [ 1.0727, 0.5418, -0.2516, -0.1133]], [[ 0.4215, 1.5712, -0.2351, 1.3741], [ 1.6418, 0.9806, -1.0259, -1.1297], [ 0.7326, 0.4989, 0.4404, 0.2975], [-0.6866, 0.5696, -0.8942, 0.6815], [ 1.7486, 0.5344, 0.0538, 0.5258]], [[ 1.6280, -1.3989, -0.2900, 0.0936], [-0.9436, -0.1766, 0.6780, 0.3152], [ 0.9645, -0.1199, -1.1644, -1.0290], [-0.2791, -0.8086, 0.2161, 0.7901], [ 1.3222, -1.4023, -2.4181, -1.2875]]]) >>> torch.einsum('bij,bjk->bik', As, Bs) tensor([[[-0.4147, -0.9847, 0.7946, -1.0103], [ 0.8020, -0.3849, 3.4942, 1.6233]], [[-1.3035, -0.5993, 0.4922, 0.9511], [-1.1150, -1.7346, 2.0142, 0.8047]], [[-1.4202, -2.5790, 4.2288, 4.5702], [-1.6549, -0.4636, 2.7802, 1.7141]]]) # with sublist format and ellipsis(带有子列表格式和省略号) >>> torch.einsum(As, [..., 0, 1], Bs, [..., 1, 2], [..., 0, 2]) tensor([[[-0.4147, -0.9847, 0.7946, -1.0103], [ 0.8020, -0.3849, 3.4942, 1.6233]], [[-1.3035, -0.5993, 0.4922, 0.9511], [-1.1150, -1.7346, 2.0142, 0.8047]], [[-1.4202, -2.5790, 4.2288, 4.5702], [-1.6549, -0.4636, 2.7802, 1.7141]]]) # batch permute(批量交换) >>> A = torch.randn(2, 3, 4, 5) >>> torch.einsum('...ij->...ji', A).shape torch.Size([2, 3, 5, 4]) # equivalent to torch.nn.functional.bilinear(等价于torch.nn.functional.bilinear) >>> A = torch.randn(3,5,4) >>> l = torch.randn(2,5) >>> r = torch.randn(2,4) >>> torch.einsum('bn,anm,bm->ba', l, A, r) tensor([[-0.3430, -5.2405, 0.4494], [ 0.3311, 5.5201, -3.0356]])









