【C++算法模板】图论-拓扑排序，超详细注释带例题

文章目录

• • 0）概述
  • 1）Kahn算法
  • • 1：数据结构
    • 2：建图
    • 3：Kanh算法
    • 2）DFS染色
    • • 1：数据结构
      • 2：建图
      • 3：DFS
      • 3）算法对比
      • 【例题】洛谷 B3644

        推荐视频链接：D01 拓扑排序

        0）概述

        • 给定一张有向无环图，排出所有顶点的一个序列 A A A 满足：对于图中的每条有向边 ( x , y ) (x,y) (x,y)， x x x 在 A A A 中都出现在 y y y 之前，则称 A A A 是该图的顶点的一个拓扑序

        • 拓扑排序 可以判断有向图中是否有环，可以生成拓扑序列

        • 对于下图， { 2 , 3 , 5 , 1 , 7 , 4 , 6 } \{2,3,5,1,7,4,6\} {2,3,5,1,7,4,6} 和 { 3 , 2 , 1 , 5 , 7 , 6 , 4 } \{3,2,1,5,7,6,4\} {3,2,1,5,7,6,4} 都是合法的拓扑序

          

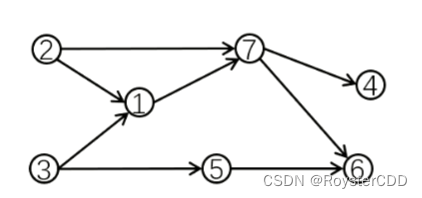
          复习一下链式前向星吧：【C++算法模板】图的存储-邻接表，手撕链式前向星，超详细代码注释-CSDN博客

          1）Kahn算法

          • 算法核心：用队列维护一个入度为 0 0 0 的节点的集合
            1. 初始化（链式前向星建图建边），队列 q q q 压入所有入度为 0 0 0 的点
            2. 每次从 q q q 中取出队头 x x x 放入数组 t p tp tp ， t p tp tp 数组保存出队顺序，也就是拓扑序
            3. 然后将 x x x 的所有出边删除，如删除边 ( x , y ) (x,y) (x,y) ， y y y 的入度则 − 1 -1 −1，如果 y y y 的入度变为 0 0 0，则将 y y y 压入 q q q 中，其中每个顶点的入度用数组 d d d 维护
            4. 不断重复 2 , 3 2,3 2,3 过程，直到队列 q q q 为空
            5. 若 t p tp tp 中的元素个数等于 n n n，则有拓扑序；否则，有环

            1：数据结构

            const int N=1e5+5; // 最大顶点数
            const int M=1e5+10; // 题目中最大边数,拓扑排序是有向图建边,无需×2
            int d[N]; // 存储每个顶点的入度
            queue q; // 维护入度为0的顶点的队列
            queue tp; // 记录q中顶点的出队顺序(拓扑序)
            int h[N]; // 存储每个顶点起始边的编号,默认-1表示无边相连
            int e[M]; // e[i]:编号为i的边可达的顶点编号
            int ne[M]; // ne[i]:编号为i的边的下一条边的编号是ne[i]
            int idx; // 边的编号,建边因子
            

            2：建图

            // 链式前向星
            void add(int a,int b) {
            	e[idx]=b;
            	ne[idx]=h[a]; // 头插法思想
            	h[a]=idx++;
            }
            

            3：Kanh算法

            // 拓扑序存储于tp队列中,如果能形成拓扑序返回true
            bool tuopu() {
            	for(int i=1;i
            		// 如果入度为0则加入队列
            		if(d[i]==0) q.push(i);
            	}
            	while(q.size()) {
            		int x=q.front();
            		q.pop();
            		tp.push(x); // 出队顺序即拓扑序
            		// 遍历x的所有出边
            		for(int i=h[x];i=-1;i=ne[i]) {
            			int j=e[i];
            			// 如果去掉边(i,j)后j的入度变为0,则加入队列
            			if(--d[j]==0) q.push(j);
            		}
            	}
            	return tp.size()==n; // 如果能形成一个拓扑序,返回true,否则false
            }
            
            	e[idx]=b;
            	ne[idx]=h[a]; // 头插法思想
            	h[a]=idx++;
            }
            
            	c[x]=-1; // 先染色为-1
            	// 遍历所有儿子节点
            	for(int i=h[x];i=-1;i=ne[i]) {
            		int j=e[i]; // 取出节点编号
            		if(c[j]
            	vector
            		// 如果c没有被走过
            		if(!c[i])
            			// 如果遇到环则说明无法形成拓扑序
            			if(!dfs(i))
            				return 0;
            	}
            	reverse(tp.begin(),tp.end());
            	return 1;
            }
            
            	e[idx]=b;
            	ne[idx]=h[a]; // 头插法思想
            	h[a]=idx++;
            }
            // 拓扑序存储于tp队列中,如果能形成拓扑序返回true
            void tuopu() {
            	queue
            		// 如果入度为0则加入队列
            		if(d[i]==0) 
            			q.push(i);
            	}
            	while(q.size()) {
            		int x=q.front();
            		q.pop();
            		cout
            			int j=e[i];
            			// 如果去掉边(i,j)后j的入度变为0,则加入队列
            			if(--d[j]==0) q.push(j);
            		}
            	}
            }
            int main() {
            	cinn;
            	memset(h,-1,sizeof h); // 链式前向星邻接表初始化
            	for(int i=1;i
            		int j;
            		// 当j==0时退出循环
            		while(cinj && j) {
            			add(i,j);
            			d[j]++; // 节点j的入度++
            		}
            	}
            	tuopu();
            	return 0;
            }