热门搜索
首页 技术支持 【Matlab】智能优化算法

【Matlab】智能优化算法

慈云数据 1年前 (2024-03-19) 技术支持 88 0

【Matlab】智能优化算法_北方苍鹰算法NGO

  • 1.背景介绍
  • 2.数学模型
    • 2.1 北方苍鹰的灵感和行为
    • 2.2 算法初始化过程
    • 2.3 NGO数学模型
      • 2.3.1 第一阶段：猎物识别（探索）
      • 2.3.2 第二阶段：追捕行动（开发）
      • 2.3.3 NGO的重复过程、伪代码和流程图
      • 3.算法流程图
      • 4.文件结构
      • 5.伪代码
      • 6.详细代码及注释
        • 6.1 fun_info.m
        • 6.2 func_plot.m
        • 6.3 main.m
        • 6.4 NGO.m
        • 7.运行结果
        • 8.参考文献

          1.背景介绍

          北方苍鹰是一种猛禽，其狩猎策略代表了一个优化过程。在这种策略中，北方苍鹰首先选择猎物并攻击它，然后在追逐过程中猎杀选定的猎物。

          本文的创新之处在于设计了一种新的基于苍鹰的优化算法，称为北方苍鹰优化（NGO），模仿北方猎鹰的行为。拟议的NGO算法的各个步骤被表达出来，然后进行数学建模。

          2.数学模型

          2.1 北方苍鹰的灵感和行为

          北方苍鹰的狩猎策略包括两个阶段，因此在第一阶段，在识别猎物后，它以高速向猎物移动，在第二阶段，它以短暂的追尾过程狩猎猎物。

          北方苍鹰在狩猎和捕捉猎物时的行为是一个智能的过程。上述策略的数学建模是设计所提出的NGO算法的主要灵感。

          2.2 算法初始化过程

          所提出的NGO是一种基于种群的算法，北方苍鹰是该算法的搜索者成员。在NGO中，每个种群成员意味着对问题的拟议解决方案，决定了变量的值。从数学的角度来看，每个人口成员是一个向量，这些向量共同构成了算法的人口矩阵。在算法的开始，人口成员在搜索空间中被随机初始化。NGO算法中的种群矩阵是用（1）确定的。

          在这里插入图片描述

          其中X是北部苍鹰的种群，Xi是第i个建议的解决方案， Xi，j是第i种建议的解决方法指定的第j个变量的值，N是种群成员的数量，m是问题变量的数量。

          如前所述，每个人口成员都是该问题的拟议解决方案。因此，可以根据每个群体成员来评估问题的目标函数。对于目标函数获得的这些值可以使用（2）表示为向量。

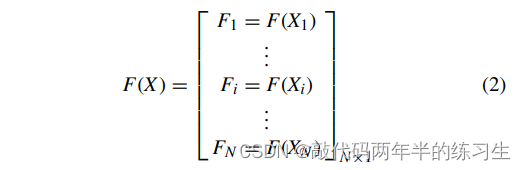
          在这里插入图片描述

          2.3 NGO数学模型

          在设计所提出的更新种群成员的非政府组织算法时，采用了北方苍鹰狩猎过程中的策略模拟。北方苍鹰在这一战略中的两个主要行为，包括

          • 猎物识别和攻击
          • 追逃行动

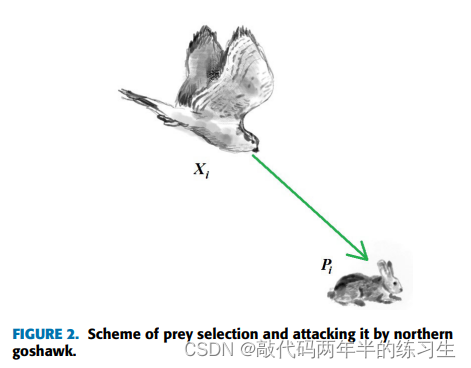
            在这里插入图片描述

            2.3.1 第一阶段：猎物识别（探索）

            北方苍鹰在狩猎的第一阶段，随机选择一个猎物，然后迅速攻击它。由于在搜索空间中随机选择猎物，这一阶段增加了NGO的探索力。该阶段导致搜索空间的全局搜索，目的是识别最优区域。图2显示了北方苍鹰在这一阶段的行为示意图，包括猎物选择和攻击。使用（3）至（5）对第一阶段中表达的概念进行数学建模。

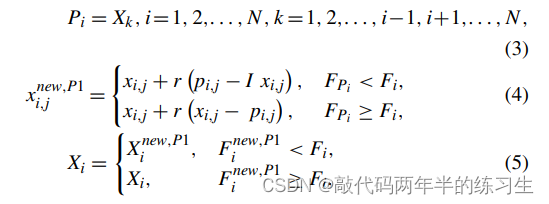
            在这里插入图片描述

            其中Pi是第i只北方苍鹰的猎物位置，FPi是其目标函数值，k是区间[1，N]中的随机自然数，X i （new，P1）是第i个提出的解的新状态，X i，j（new，P1）是其第j维，F i（new，P1）是其基于NGO第一阶段的目标函数值；r是区间[0，1]中的随机数，I是一个随机数，可以是1或2。参数r和I是用于在搜索和更新中生成随机NGO行为的随机数。

            2.3.2 第二阶段：追捕行动（开发）

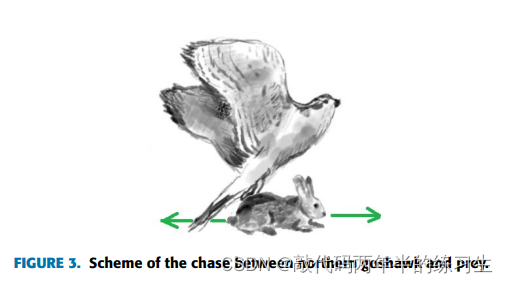
            在北方苍鹰攻击猎物后，猎物会试图逃跑。因此，在尾随和追赶的过程中，北方苍鹰继续追赶猎物。由于北方苍鹰的高速度，它们几乎可以在任何情况下追赶猎物，并最终猎获。对这种行为的模拟增加了算法对搜索空间的局部搜索的开发能力。在所提出的NGO算法中，假定这种狩猎是封闭在半径为R的攻击位置，北方苍鹰和猎物之间的追逐过程如图3所示。第二阶段所表达的概念用（6）到（8）进行了数学建模。

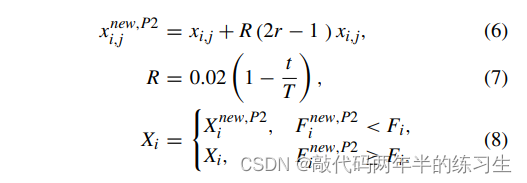
            在这里插入图片描述

            其中，t是迭代计数器，t是最大迭代次数，X i（new，P2）是第i个提出的解决方案的新状态，X i，j（new，P2）是其第j个维度，F i（next，P2）是其基于NGO第二阶段的目标函数值。

            在这里插入图片描述

            2.3.3 NGO的重复过程、伪代码和流程图

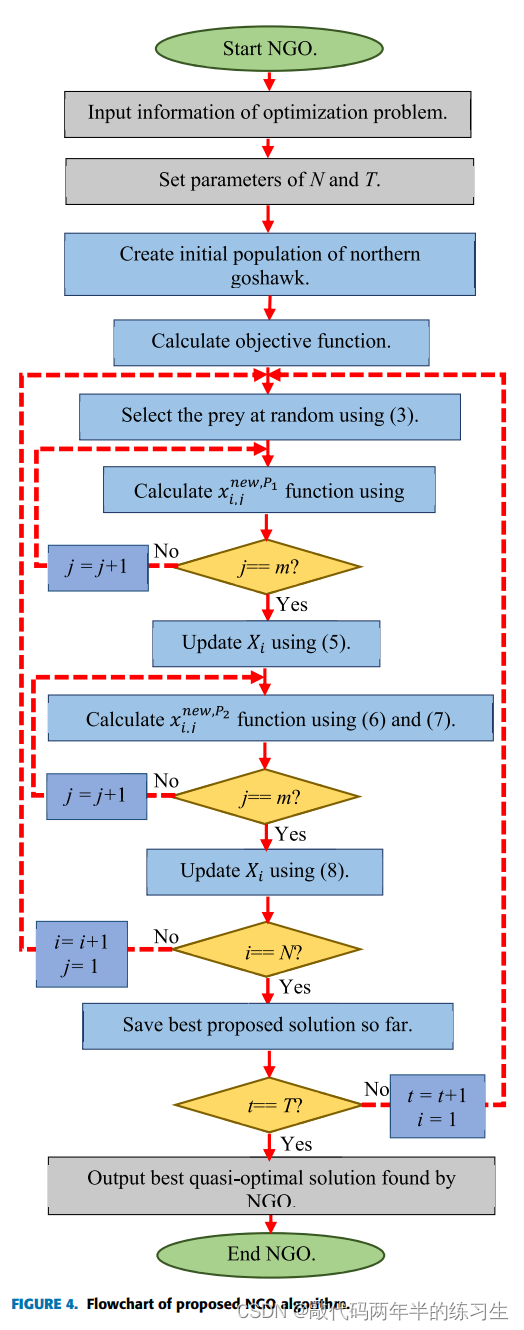
            在基于所提出的NGO算法的第一和第二阶段更新了群体的所有成员之后，完成了算法的迭代，并确定了群体成员的新值、目标函数和所提出的最佳解。然后算法进入下一次迭代，并且种群成员基于等式（3）至（8）继续更新，直到达到算法的最后一次迭代。最后，在NGO完全实现后，将算法迭代过程中获得的最佳解作为给定优化问题的拟最优解。所提出的NGO算法的各个阶段在算法1中被指定为伪代码，其流程图如图4所示。

            3.算法流程图

            在这里插入图片描述

            4.文件结构

            在这里插入图片描述

            fun_info.m						% 基准函数信息
func_plot.m						% 绘制的基准函数
NGO.m							% 北方苍鹰优化算法
main.m							% 主函数

            5.伪代码

            在这里插入图片描述

            6.详细代码及注释

            6.1 fun_info.m

            function [lowerbound,upperbound,dimension,fitness] = fun_info(F)
switch F
    case 'F1'
        fitness = @F1;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F2'
        fitness = @F2;
        lowerbound=-10;
        upperbound=10;
        dimension=30;
        
    case 'F3'
        fitness = @F3;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F4'
        fitness = @F4;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F5'
        fitness = @F5;
        lowerbound=-30;
        upperbound=30;
        dimension=30;
        
    case 'F6'
        fitness = @F6;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F7'
        fitness = @F7;
        lowerbound=-1.28;
        upperbound=1.28;
        dimension=30;
        
    case 'F8'
        fitness = @F8;
        lowerbound=-500;
        upperbound=500;
        dimension=30;
        
    case 'F9'
        fitness = @F9;
        lowerbound=-5.12;
        upperbound=5.12;
        dimension=30;
        
    case 'F10'
        fitness = @F10;
        lowerbound=-32;
        upperbound=32;
        dimension=30;
        
    case 'F11'
        fitness = @F11;
        lowerbound=-600;
        upperbound=600;
        dimension=30;
        
    case 'F12'
        fitness = @F12;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F13'
        fitness = @F13;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F14'
        fitness = @F14;
        lowerbound=-65.536;
        upperbound=65.536;
        dimension=2;
        
    case 'F15'
        fitness = @F15;
        lowerbound=-5;
        upperbound=5;
        dimension=4;
        
    case 'F16'
        fitness = @F16;
        lowerbound=-5;
        upperbound=5;
        dimension=2;
        
    case 'F17'
        fitness = @F17;
        lowerbound=[-5,0];
        upperbound=[10,15];
        dimension=2;
        
    case 'F18'
        fitness = @F18;
        lowerbound=-2;
        upperbound=2;
        dimension=2;
        
    case 'F19'
        fitness = @F19;
        lowerbound=0;
        upperbound=1;
        dimension=3;
        
    case 'F20'
        fitness = @F20;
        lowerbound=0;
        upperbound=1;
        dimension=6;     
        
    case 'F21'
        fitness = @F21;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F22'
        fitness = @F22;
        lowerbound=0;
        upperbound=10;
        dimension=4;    
        
    case 'F23'
        fitness = @F23;
        lowerbound=0;
        upperbound=10;
        dimension=4;            
end
end
% F1
function R = F1(x)
R=sum(x.^2);
end
% F2
function R = F2(x)
R=sum(abs(x))+prod(abs(x));
end
% F3
function R = F3(x)
dimension=size(x,2);
R=0;
for i=1:dimension
    R=R+sum(x(1:i))^2;
end
end
% F4
function R = F4(x)
R=max(abs(x));
end
% F5
function R = F5(x)
dimension=size(x,2);
R=sum(100*(x(2:dimension)-(x(1:dimension-1).^2)).^2+(x(1:dimension-1)-1).^2);
end
% F6
function R = F6(x)
R=sum(abs((x+.5)).^2);
end
% F7
function R = F7(x)
dimension=size(x,2);
R=sum([1:dimension].*(x.^4))+rand;
end
% F8
function R = F8(x)
R=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function R = F9(x)
dimension=size(x,2);
R=sum(x.^2-10*cos(2*pi.*x))+10*dimension;
end
% F10
function R = F10(x)
dimension=size(x,2);
R=-20*exp(-.2*sqrt(sum(x.^2)/dimension))-exp(sum(cos(2*pi.*x))/dimension)+20+exp(1);
end
% F11
function R = F11(x)
dimension=size(x,2);
R=sum(x.^2)/4000-prod(cos(x./sqrt([1:dimension])))+1;
end
% F12
function R = F12(x)
dimension=size(x,2);
R=(pi/dimension)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dimension-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dimension)+1)./4)))).^2))+((x(dimension)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function R = F13(x)
dimension=size(x,2);
R=.1*((sin(3*pi*x(1)))^2+sum((x(1:dimension-1)-1).^2.*(1+(sin(3.*pi.*x(2:dimension))).^2))+...
((x(dimension)-1)^2)*(1+(sin(2*pi*x(dimension)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function R = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
    bS(j)=sum((x'-aS(:,j)).^6);
end
R=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function R = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
R=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function R = F16(x)
R=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function R = F17(x)
R=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function R = F18(x)
R=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function R = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function R = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
R=0;
for i=1:4
    R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function R = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;
for i=1:5
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function R = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;
for i=1:7
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function R = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;
for i=1:10
    R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function R=Ufun(x,a,k,m)
R=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x
海报

猜你喜欢

php redis分布式锁

php redis分布式锁
linux内存缓存占用过高分析和优化

linux内存缓存占用过高分析和优化
stm32编写Modbus步骤

stm32编写Modbus步骤
如何保证数据库和缓存的一致性

如何保证数据库和缓存的一致性
Mongodb聚合操作中的$unset

Mongodb聚合操作中的$unset
私域引流宝PHP源码 以及搭建教程

私域引流宝PHP源码 以及搭建教程
400-801-9632
微信扫一扫加客服

微信扫一扫加客服

851239876