Unity中的网格创建和曲线变形
- 3D贝塞尔曲线变形
- 贝塞尔曲线基础
- 线性公式
- 二次方公式
- 三次方公式
- Unity 实现3D贝塞尔曲线变形
- 准备工作
- 脚本概述
- 变量定义
- 变量解析
- 函数解析 获取所有子节点
- GetAllChildren 获取所有子节点
- UpdateBezierBend 控制点更新
- CalculateBezier Bezier 曲线公式
- GetBendNormalVector 获取指定点上的法线向量偏移
- UpdateControlPoint 更新控制点的旋转角度
- CalculateBezierTangent 曲线求导(切线向量)
- BesselCurveDeformation_ZH 完整代码
- 自定义网格创建
- GridCreation_ZH 完整代码
- GridCreation_ZH 搭载
- 自定义网格创建 运行效果
- 网格创建和曲线变形 运行情况
在本篇博客中,我们将探讨如何使用Unity实现3D贝塞尔曲线变形效果。
3D贝塞尔曲线变形
贝塞尔曲线是一种常用的数学曲线,通过控制点和曲线影响力物体我们可以实现对网格的弯曲和变形。 在示例代码中,我们可以看到通过设置控制点数组、曲线影响力物体和控制物体曲线施加力等变量。 实现了对网格进行贝塞尔曲线变形的效果。这种技术在游戏中常用于创建动态的形变效果。 如弯曲的绳索、变形的角色模型等。
贝塞尔曲线基础
贝塞尔曲线是一种由控制点定义的数学曲线。 在3D空间中,我们通常使用3次贝塞尔曲线,它由四个控制点(起始点、两个中间点和结束点)组成。
贝塞尔曲线的形状受控制点的位置和权重影响。 控制点的位置决定了曲线经过的路径,而权重控制了曲线在控制点之间的弯曲程度。
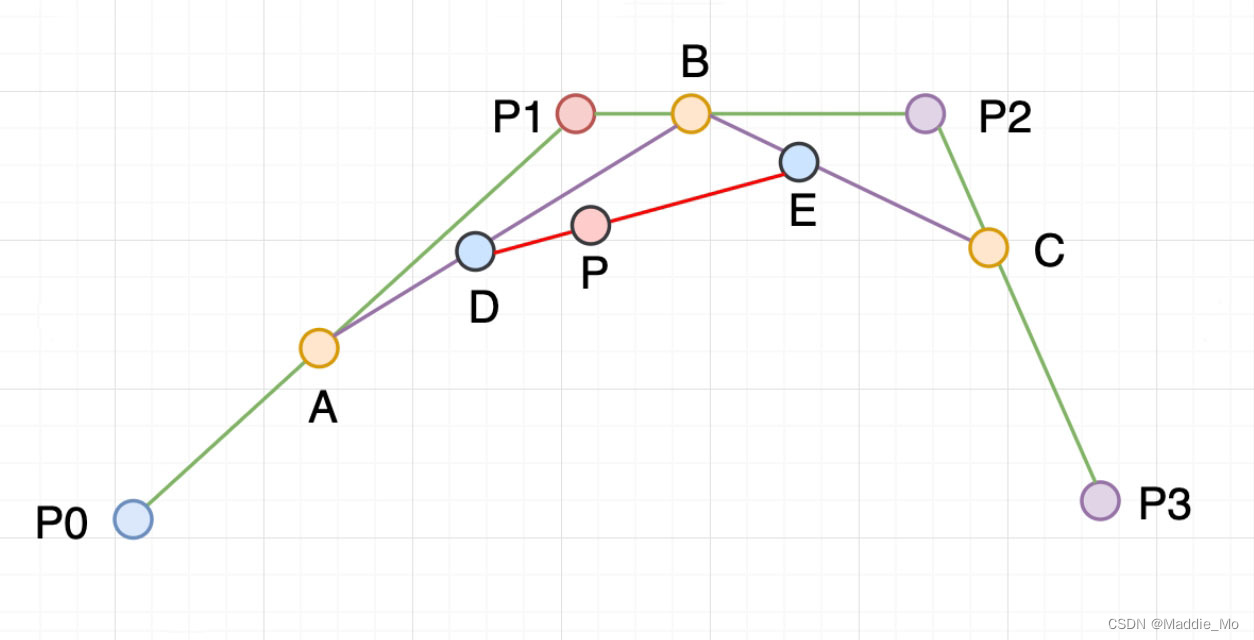
线性公式
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。
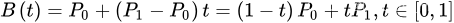
二次方公式
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪: TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。
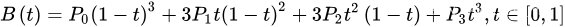
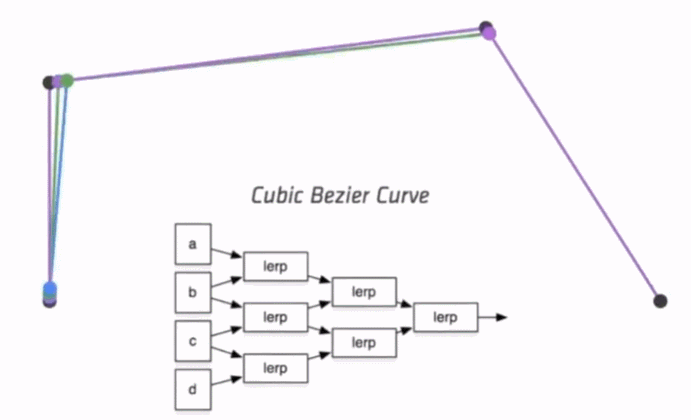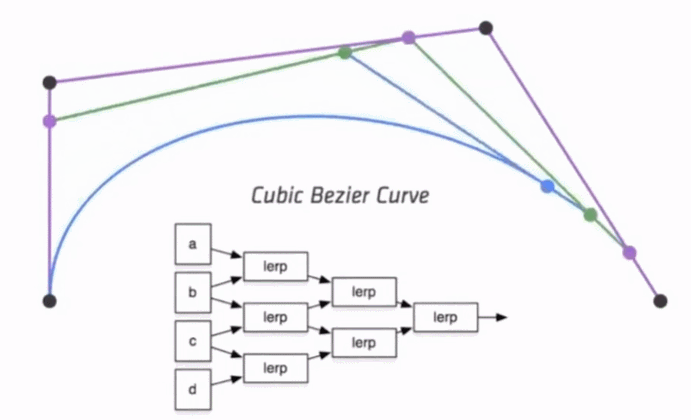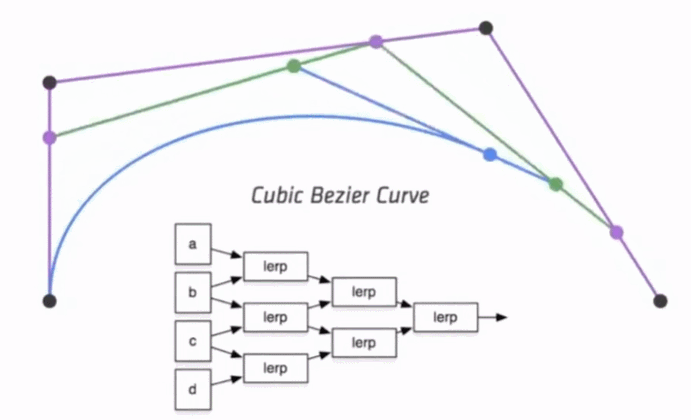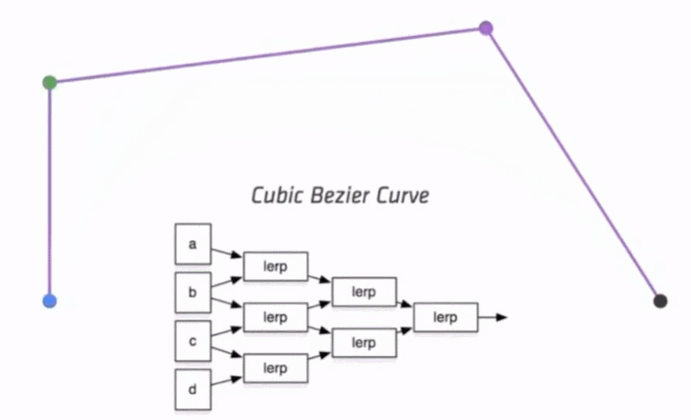
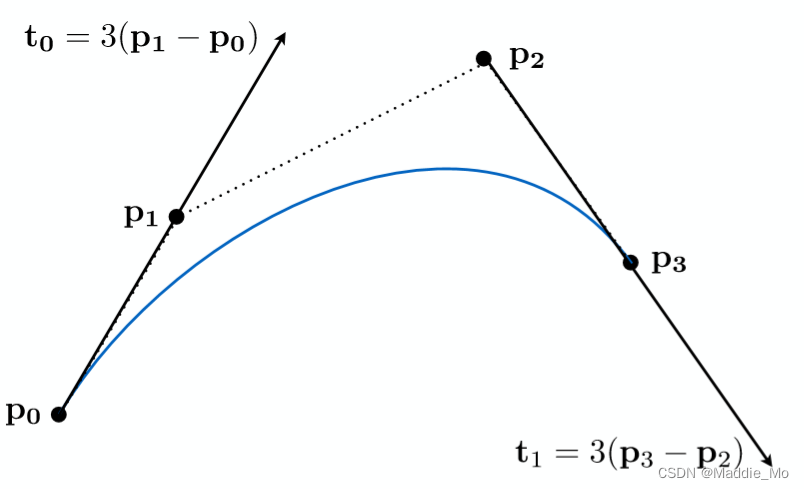
三次方公式
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。 曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2。 这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前 走向P2方向的“长度有多长”。
曲线的参数形式为:
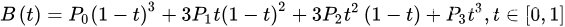
现代的成象系统,如PostScript、Asymptote和Metafont 运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
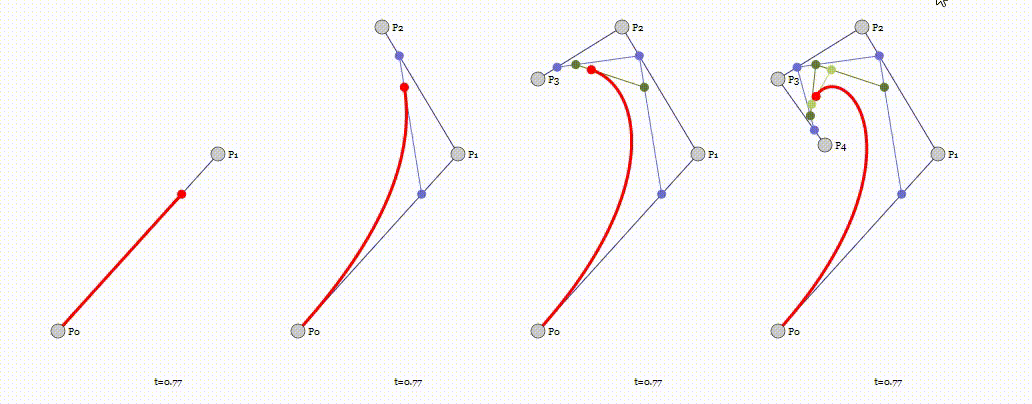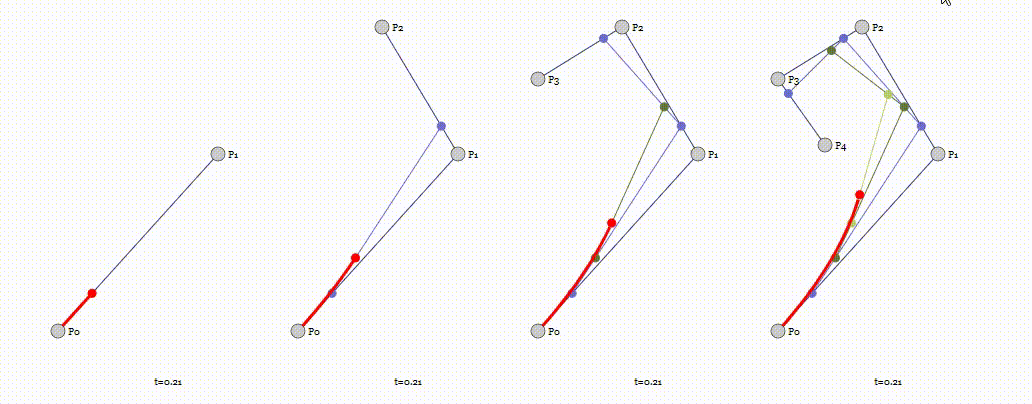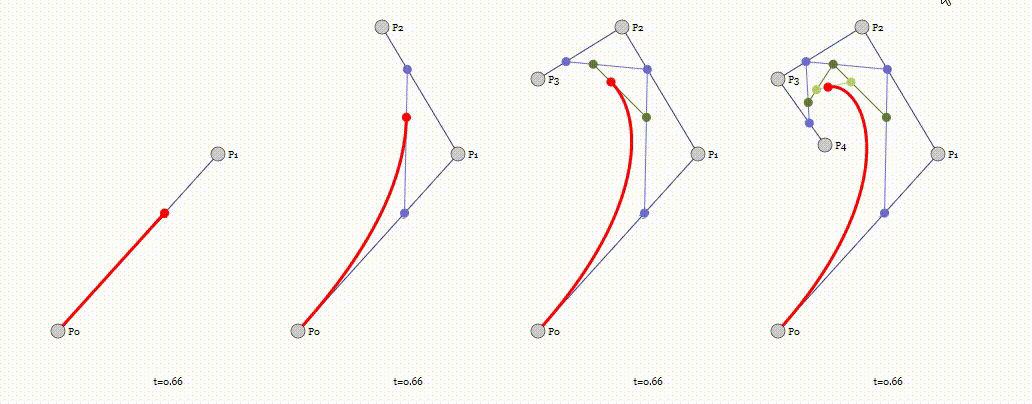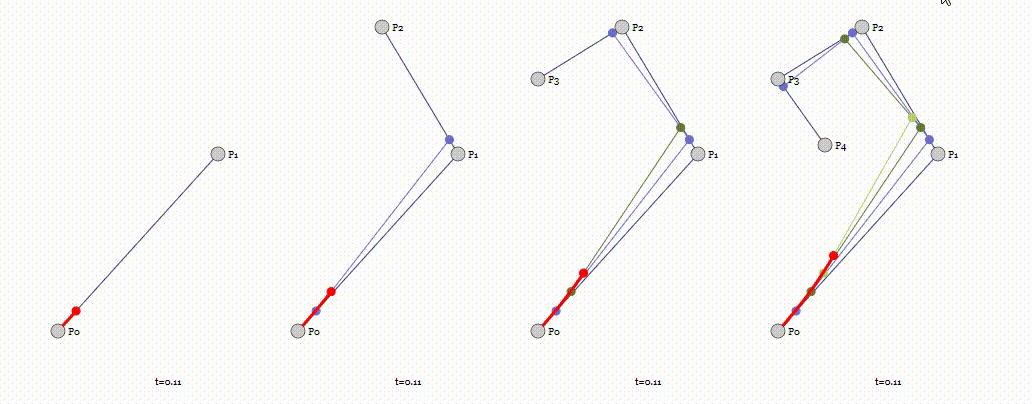
Unity 实现3D贝塞尔曲线变形
准备工作
首先,我们需要在Unity中创建一个空的GameObject,并将该脚本附加到该GameObject上。 接下来,我们需要创建一个网格,可以通过导入一个3D模型或者使用Unity内置的网格创建工具来完成。
脚本概述
让我们先来看一下脚本的整体结构: 1.变量定义 2.Start()函数 2.Update()函数 3.初始化函数 4.获取所有子节点函数 5.贝塞尔曲线Mesh计算相关函数
变量定义
[Header("存储贝塞尔曲线控制点数组")] public List _CpArr; [Header("曲线影响力物体")] public Transform _ForceItem; [Range(0, 100f)] [Header("控制物体曲线施加力")] public float _Force = 10; [Header("原始顶点位置")] private Vector3[] _OriVertices; [Header("网格数据")] private Mesh _Mesh; [Header("最后一个控制点位置")] //最后一个控制点的位置。用来计算mesh高度来计算t private Vector3 _TopPos;变量解析
_CpArr: 存储贝塞尔曲线控制点数组的列表。 _ForceItem: 曲线影响力物体的Transform组件。 _Force: 控制物体曲线施加力的大小,范围在0到100之间。 _OriVertices: 原始顶点位置的数组。 _Mesh: 网格数据的Mesh组件。 _TopPos: 最后一个控制点的位置,用于计算mesh高度来计算t。
函数解析 获取所有子节点
Start(): 在脚本启动时调用,用于初始化操作。 Update(): 在每一帧更新时调用,用于更新控制点和网格。 Initialize(): 初始化函数,用于设置控制点数组和作用力变量等。
GetAllChildren 获取所有子节点
GetAllChildren: 获取所有子节点的函数,用于递归收集父节点下的所有子节点。
/// /// 获取所有子节点 /// /// /// private List GetAllChildren(Transform _Parent) { List _ListTra = new List(); foreach (Transform _Child in _Parent) { //添加直接子节点 _ListTra.Add(_Child); //递归收集后代节点 List _Descendants = GetAllChildren(_Child); _ListTra.AddRange(_Descendants); } return _ListTra; }UpdateBezierBend 控制点更新
UpdateBezierBend: 控制点更新函数,根据施加在曲线上的力,计算并更新控制点的旋转角度。
/// /// 控制点更新 /// 根据施加在曲线上的力,计算并更新控制点的旋转角度 /// private void UpdateBezierBend() { //曲线弯曲方向 Vector3 _BendVector = new Vector3(0, 0, 0); //弯曲布尔 true 无弯曲 false 弯曲 bool _IsVertical = true; for (int i = 1; iCalculateBezier Bezier 曲线公式
CalculateBezier: Bezier曲线公式计算函数,根据给定的t值计算贝塞尔曲线上的点坐标。
/// /// Bezier 曲线公式 /// 计算贝塞尔曲线上给定参数值 _CurvePosition 对应的位置 /// /// /// private Vector3 CalculateBezier(float _CurvePosition) { //存储坐标 Vector3 _Ret = new Vector3(0, 0, 0); //控制点数量 int _Number = _CpArr.Count - 1; for (int i = 0; i //获取第 i 个控制点的世界坐标,通过将其位置从控制点的局部坐标系转换到世界坐标 Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0)); //将转换后的世界坐标再次转换回第一个控制点的局部坐标系,用于与其他控制点进行计算 _Pi = _CpArr[0].InverseTransformPoint(_Pi); //根据贝塞尔曲线的定义,计算贝塞尔基函数的乘积项,并与控制点的局部坐标相乘 //Cn_m(_Number, i) 是组合数函数 表示从 _Number 个控制点中选择 i 个的组合数 _Ret = _Ret + Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi; } return _Ret; } //切线斜率 Vector3 _TangentVector = CalculateBezierTangent(_CurvePosition); //切线竖直时,顶点在在弯曲向量上的投影向量即为法线向量 if (IsEqualZero(_TangentVector.x) == true && IsEqualZero(_TangentVector.z) == true) { //直接返回 原始位置 _OriPos 投影到弯曲向量 _BendVector 上的向量,作为法线向量 return Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector); } //存储计算得到的法线向量 Vector3 _NormalVector = new Vector3(0, 0, 0); //计算切线向量与原始位置向量的点乘 float _DirectFlag = Vector3.Dot(_BendVector, _OriPos); //判断法线向量朝向(法线向量有两个方向) //大于零 顶点坐标与弯曲方向同向 if (_DirectFlag 0) { //切线水平,法线向量竖直向下 if (IsEqualZero(_TangentVector.y) == true) { _NormalVector.y = -1; } else { //切线朝上,法线向量与切线水平同向 if (_TangentVector.y > 0) { _NormalVector.x = _TangentVector.x; _NormalVector.z = _TangentVector.z; } //切线朝下,法线向量与切线水平反向 else { _NormalVector.x = -_TangentVector.x; _NormalVector.z = -_TangentVector.z; } //使法线向量与切线向量水平且垂直于切线向量 _NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y; } } //小于零 顶点坐标与弯曲方向反向 else { //切线水平,法线向量竖直向上 if (IsEqualZero(_TangentVector.y) == true) { _NormalVector.y = 1; } else { //切线朝上,法线向量与切线水平反向 if (_TangentVector.y > 0) { _NormalVector.x = -_TangentVector.x; _NormalVector.z = -_TangentVector.z; } //切线朝下,法线向量与切线水平同向 else { _NormalVector.x = _TangentVector.x; _NormalVector.z = _TangentVector.z; } //使得法线向量与切线向量水平且垂直于切线向量 _NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y; } } //计算法线向量的模 //法线向量的模应为到投影到弯曲面后,到中心点的距离 float _Magnitude = Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector).magnitude; //将法线向量按照该模进行缩放,使其长度与距离一致 _NormalVector = _NormalVector.normalized * _Magnitude; //返回法线向量 return _NormalVector; }UpdateControlPoint 更新控制点的旋转角度
UpdateControlPoint: 控制点更新函数,根据施加在曲线上的力,计算并更新控制点的位置。
/// /// 更新控制点的旋转角度 /// 根据受力计算各个控制点的旋转角度 /// private void UpdateControlPoint() { //受力强度 float _HandleForce = _Force; //根据受力计算各个控制点旋转角度 for (int i = 1; i //计算最大弯曲方向 Vector3 _ForcePos = _ForceItem.transform.TransformPoint(new Vector3(0, 0, 0)); _ForcePos = _CpArr[i - 1].InverseTransformPoint(_ForcePos); //计算从控制点到受力位置的向量 Vector3 _ToVector = _ForcePos - _CpArr[i].localPosition; //得到该控制点的旋转角度 Quaternion _MaxRotation = Quaternion.FromToRotation(Vector3.up, _ToVector); //获取控制点组件 ControlPoint_ZH _Cp = _CpArr[i].gameObject.GetComponent //存储计算得到的切线向量 Vector3 _Ret = new Vector3(0, 0, 0); //控制点数量 int _Number = _CpArr.Count - 1; for (int i = 0; i Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0)); _Pi = _CpArr[0].InverseTransformPoint(_Pi); //根据贝塞尔曲线的定义,计算贝塞尔基函数的导数项,并与控制点的局部坐标相乘 //每次循环迭代,都将计算得到的导数项加到 _Ret 向量上 _Ret = _Ret + (-1 * (_Number - i) * Mathf.Pow(1 - _CurvePosition, _Number - i - 1) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi + i * Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i - 1) * Cn_m(_Number, i) * _Pi); } //返回计算得到的切线向量 _Ret,表示贝塞尔曲线上给定参数值 _CurvePosition 对应的切线向量 return _Ret; } [Header("存储贝塞尔曲线控制点数组")] public List Initialize(); } void Update() { //根据受力,修改控制点 UpdateControlPoint(); //更新mesh UpdateBezierBend(); } /// //初始化 控制点数组 _CpArr = new List // //数组清空 // _CpArr.Clear(); // //获取所有控制端点 // _CpArr = GetAllChildren(GameObject.Find("Node").transform); //} //else { GameObject _EmptyObject0 = new GameObject("P0"); GameObject _EmptyObject1 = new GameObject("P1"); GameObject _EmptyObject2 = new GameObject("P2"); GameObject _EmptyObject3 = new GameObject("P3"); GameObject _EmptyObject4 = new GameObject("P4"); GameObject _EmptyObject5 = new GameObject("P5"); _EmptyObject0.transform.SetParent(transform); _EmptyObject0.transform.localPosition=new Vector3(GridCreation_ZH._Instance._MeshHeight/2*-1, 0,0); _EmptyObject1.transform.SetParent(_EmptyObject0.transform); _EmptyObject1.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight/6, 0); _EmptyObject2.transform.SetParent(_EmptyObject1.transform); _EmptyObject2.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0); _EmptyObject3.transform.SetParent(_EmptyObject2.transform); _EmptyObject3.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0); _EmptyObject4.transform.SetParent(_EmptyObject3.transform); _EmptyObject4.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0); _EmptyObject5.transform.position = new Vector3(0, GridCreation_ZH._Instance._MeshHeight, 0); //_EmptyObject5.transform.eulerAngles=new Vector3(0, 0, 90); _EmptyObject5.transform.SetParent(_EmptyObject4.transform); _CpArr.Add(_EmptyObject0.transform); _CpArr.Add(_EmptyObject1.transform); _CpArr.Add(_EmptyObject2.transform); _CpArr.Add(_EmptyObject3.transform); _CpArr.Add(_EmptyObject4.transform); _CpArr.Add(_EmptyObject5.transform); for (int i = 0; i









