1686. 石子游戏 VI
Alice 和 Bob 轮流玩一个游戏,Alice 先手。
一堆石子里总共有 n 个石子,轮到某个玩家时,他可以 移出 一个石子并得到这个石子的价值。Alice 和 Bob 对石子价值有 不一样的的评判标准 。双方都知道对方的评判标准。
给你两个长度为 n 的整数数组 aliceValues 和 bobValues 。aliceValues[i] 和 bobValues[i] 分别表示 Alice 和 Bob 认为第 i 个石子的价值。
所有石子都被取完后,得分较高的人为胜者。如果两个玩家得分相同,那么为平局。两位玩家都会采用 最优策略 进行游戏。
请你推断游戏的结果,用如下的方式表示:
如果 Alice 赢,返回 1 。
如果 Bob 赢,返回 -1 。
如果游戏平局,返回 0 。
示例 1:
输入:aliceValues = [1,3], bobValues = [2,1]
输出:1
解释:
如果 Alice 拿石子 1 (下标从 0开始),那么 Alice 可以得到 3 分。
Bob 只能选择石子 0 ,得到 2 分。
Alice 获胜。
示例 2:
输入:aliceValues = [1,2], bobValues = [3,1]
输出:0
解释:
Alice 拿石子 0 , Bob 拿石子 1 ,他们得分都为 1 分。
打平。
示例 3:
输入:aliceValues = [2,4,3], bobValues = [1,6,7]
输出:-1
解释:
不管 Alice 怎么操作,Bob 都可以得到比 Alice 更高的得分。
比方说,Alice 拿石子 1 ,Bob 拿石子 2 , Alice 拿石子 0 ,Alice 会得到 6 分而 Bob 得分为 7 分。
Bob 会获胜。
提示:
n == aliceValues.length == bobValues.length
1 public: int stoneGameVI(vector int n = aliceValues.size(); vector diff[i] = {aliceValues[i] + bobValues[i], i}; } sort(diff.begin(), diff.end(), greater int idx = diff[i].second; if (i % 2 == 0) { aliceScore += aliceValues[idx]; } else { bobScore += bobValues[idx]; } } if (aliceScore bobScore) { return 1; } else if (aliceScore right->val = next_level_sum - children_sum; } q = move(nxt); } return root; } };
题解:BFS+算两次
993. 二叉树的堂兄弟节点
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
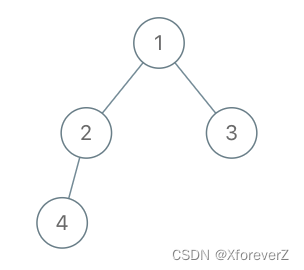
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
示例 2:
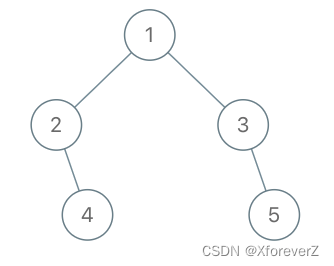
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
示例 3:
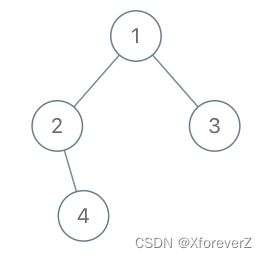
输入:root = [1,2,3,null,4], x = 2, y = 3
输出:false
提示:
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。
深度优先搜索DFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
bool isCousins(TreeNode* root, int x, int y) {
bool ans = false;
int depth = 0;
TreeNode* father = nullptr;
function dfs =
[&](TreeNode* node, TreeNode* fa, int d) -> bool {
if (node == nullptr) {
return false;
}
if (node->val == x || node->val == y) {
if (depth) {
ans = depth == d && father != fa;
return true;
}
depth = d;
father = fa;
}
return dfs(node->left, node, d + 1) ||
dfs(node->right, node, d + 1);
};
dfs(root, nullptr, 1);
return ans;
}
};
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
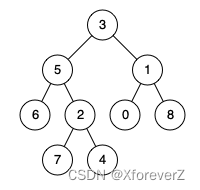
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
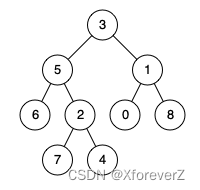
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 1e5] 内。
-1e9 public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if (root == nullptr || root == p || root == q) { return root; } auto left = lowestCommonAncestor(root-left, p, q); auto right = lowestCommonAncestor(root-right, p, q); if (left && right) { return root; } return left ? left : right; } };
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
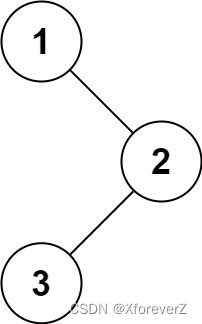
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
树中节点数目在范围 [0, 100] 内
-100 void midorder(TreeNode* cur, vector if (cur == NULL) { return; } midorder(cur-left, vec); vec.push_back(cur-val); midorder(cur->right, vec); } public: vector inorderTraversal(TreeNode* root) { vector vec; midorder(root, vec); return vec; } };
144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
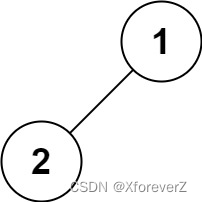
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
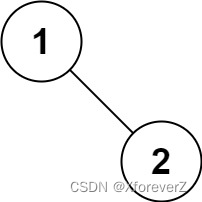
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 public: void preorder(TreeNode* root, vector if (root == NULL) { return; } vec.push_back(root-val); preorder(root-left, vec); preorder(root->right, vec); } vector preorderTraversal(TreeNode* root) { vector vec; preorder(root, vec); return vec; } };
145. 二叉树的后序遍历
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
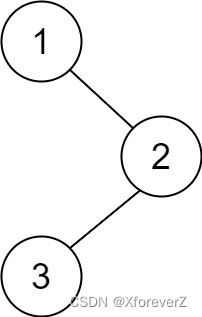
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
树中节点的数目在范围 [0, 100] 内
-100 public: void lastorder(TreeNode *cur,vector if(cur==NULL){ return; } lastorder(cur-left,vec); lastorder(cur-right,vec); vec.push_back(cur->val); } vector postorderTraversal(TreeNode* root) { vector vec; lastorder(root,vec); return vec; } };
987. 二叉树的垂序遍历
给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
返回二叉树的 垂序遍历 序列。
示例 1:
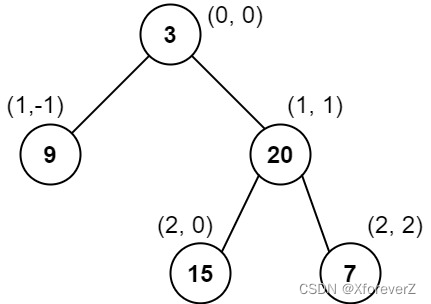
输入:root = [3,9,20,null,null,15,7]
输出:[[9],[3,15],[20],[7]]
解释:
列 -1 :只有结点 9 在此列中。
列 0 :只有结点 3 和 15 在此列中,按从上到下顺序。
列 1 :只有结点 20 在此列中。
列 2 :只有结点 7 在此列中。
示例 2:
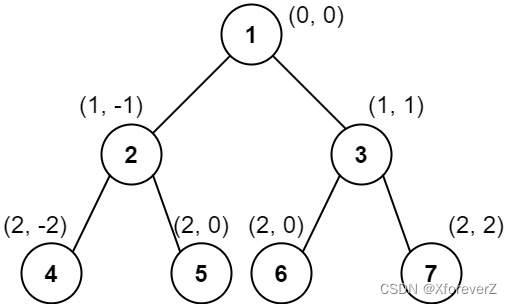
输入:root = [1,2,3,4,5,6,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
列 -2 :只有结点 4 在此列中。
列 -1 :只有结点 2 在此列中。
列 0 :结点 1 、5 和 6 都在此列中。
1 在上面,所以它出现在前面。
5 和 6 位置都是 (2, 0) ,所以按值从小到大排序,5 在 6 的前面。
列 1 :只有结点 3 在此列中。
列 2 :只有结点 7 在此列中。
示例 3:
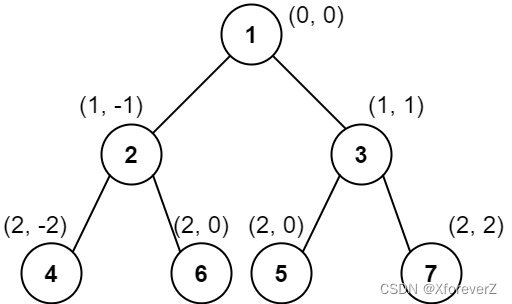
输入:root = [1,2,3,4,6,5,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
这个示例实际上与示例 2 完全相同,只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同,所以答案保持不变,仍然按值从小到大排序。
提示:
树中结点数目总数在范围 [1, 1000] 内
0 map if (node == nullptr) { return; } groups[col].emplace_back(row, node-val); dfs(node-left, row + 1, col - 1); dfs(node->right, row + 1, col + 1); } public: vector verticalTraversal(TreeNode* root) { dfs(root, 0, 0); vector ans; for (auto& [_, g] : groups) { ranges::sort(g); vector vals; for (auto& [_, val] : g) { vals.push_back(val); } ans.push_back(vals); } return ans; } };
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
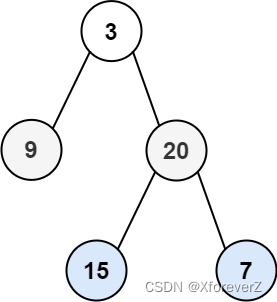
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 public: vector queue int size = que.size(); vector TreeNode* node = que.front(); que.pop(); vec.push_back(node-val); if (node-left) que.push(node->left); if (node->right) que.push(node->right); } result.push_back(vec); } return result; } };
107. 二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
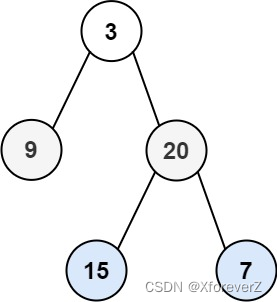
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 public: vector queue int size = que.size(); vector TreeNode* node = que.front(); que.pop(); vec.push_back(node-val); if (node-left) que.push(node->left); if (node->right) que.push(node->right); } result.push_back(vec); } reverse(result.begin(), result.end()); return result; } };









