函数递归详解青蛙跳台阶问题😎
- 函数递归之青蛙跳台阶详解分析🙌
- 青蛙跳台阶的问题是什么样的问题?😊
- 青蛙跳台阶的跳动图解:🙌
- 总结撒花💞
哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
函数递归之青蛙跳台阶详解分析🙌
青蛙跳台阶的问题是什么样的问题?😊
青蛙跳台阶问题简述: 😍
一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶。例如:跳上第一级台阶只有一种跳法:直接跳 1 级即可。跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级。问要跳上第 n 级台阶有多少种跳法?

青蛙跳台阶的跳动图解:🙌
看了上述文字讲解,大家可能还是不够理解,这里已3层台阶为例,分析青蛙跳法和具体过程: 😍
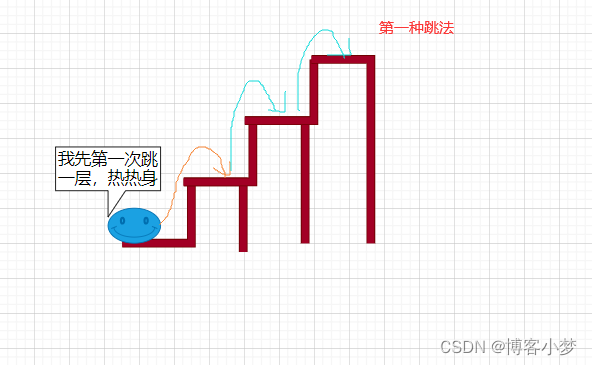
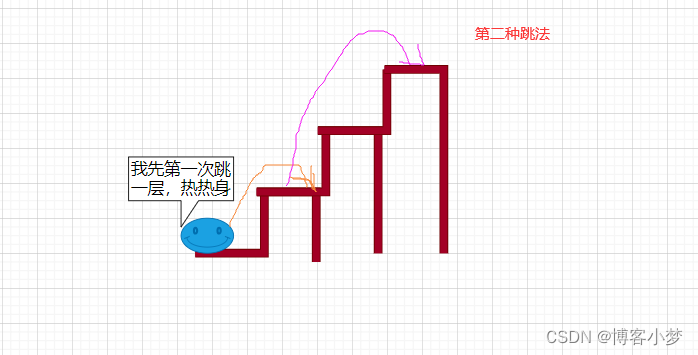
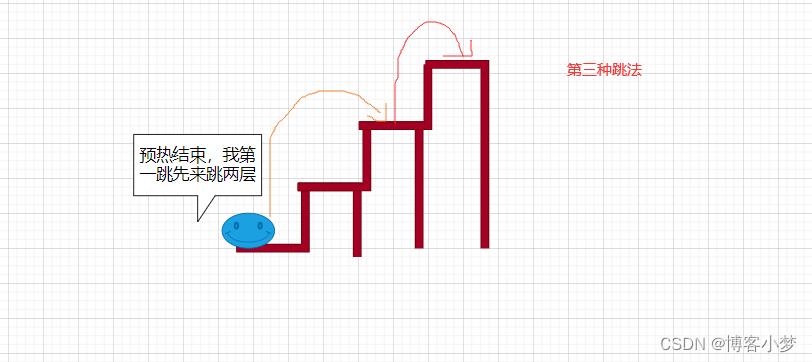
理清楚思路之后,我们不能发现,青蛙跳台阶的问题也是可以通过函数递归的方法来实现的。
青蛙跳台阶递归代码实现: 😍
int Frog(int n) { if (n == 1) return 1; else if (n == 2) return 2; else if (n >= 3) return Frog(n - 1) + Frog(n - 2); } #include int main() { int n = 0; scanf("%d", &n); int ways = Frog(n); printf("跳%d阶台阶方法总数为:%d\n", n, ways); return 0; }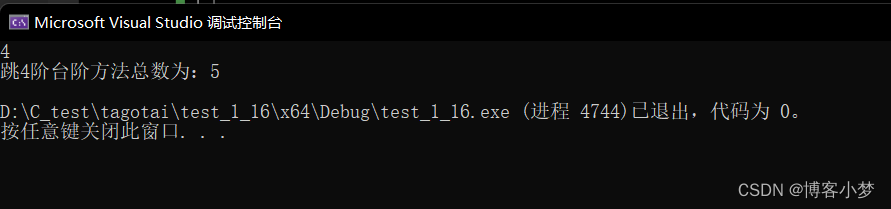
当 n = 4时
Frog (4)
= Frog(3)+ Frog(2)
= Frog (2) + Frog(1)+ Frog(2)
= 2 + 1 +2
= 5
总结撒花💞
青蛙跳台阶的问题,其实和求斐波那契数列的方法很相似,大家对比理解一下就好啦!本篇文章旨在带领大家使用函数递归的知识来求解经典的青蛙跳台阶问题。希望大家通过阅读此文有所收获!😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘








