手撕链表OJ

𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary-walk

      ⸝⋆   ━━━┓

     - 个性标签 - ：来于“云”的“羽球人”。 Talk is cheap. Show me the code

┗━━━━━━━  ➴ ⷯ

本人座右铭 ：   欲达高峰,必忍其痛;欲戴王冠,必承其重。

👑💎💎👑💎💎👑 

💎💎💎自💎💎💎

💎💎💎信💎💎💎

👑💎💎　💎💎👑    希望在看完我的此篇博客后可以对你有帮助哟

👑👑💎💎💎👑👑   

👑👑👑💎👑👑👑

目录：

一 ​​​​​​移除链表元素

二：反转一个单链表

三：链表的中间结点

四：链表中倒数第k个结点

五：合并两个有序链表

六：链表分割

七：链表的回文结构

八：相交链表

题目：

九： 环形链表

十：环形链表 II

 十一：

 1： ​​​​​​移除链表元素

思路分析 

这里咱有2中方法可以实现：

方法1：直接在原链表进行删除

总的方向：把等于val 的对应节点直接删除即可，定义三个指针：pre(当前指针的前一个节点),del（要删除的节点),cur（当前节点）

注意细节：

1）当链表第一个节点就需要删除 也就是说  pre == NULL,这时候头结点需要更新

2）正常情况的删除:改变pre指向节点的next ,这时候需要找到删除cur这个节点的前一个节点也就是pre

3非头结点并且也不需要删除：pre依次改变   即 pre = cur

对应草图如下：

OJ代码

struct ListNode* removeElements(struct ListNode* head, int val)
 {
    struct ListNode* cur = head,*pre = NULL,*del = NULL;
    while(cur)
    {
        if(cur->val == val)
        {
            if(pre == NULL)//头结点的删除
            {
                del = cur;
                cur = del->next;
              head = cur;//更新头结点
                free(del);
            }
            else
            {
                del= cur;
                cur = del->next;
                pre->next = cur;
                free(del);
        
            }
            
        }
        else
        {
            //不需删除
            pre = cur;
            cur = cur->next;
        }
    }
    return head;
}

方法2：借助链表尾插函数的思想，把不为 val对应的节点取下来进行尾插

那么问题来了：每次尾插之前都需要先找尾，在时间上就很不占优势n个节点那么对应时间复杂度就是 O(N^2) 

这里我们就需要定义一个tail指针，以此解决此问题

总的方向：不是val的节点拿下来尾插，定义三个指针  tail(尾指针) newhead(新的头结点)cur(指向原链表的当前节点)

注意细节：

1）第一个节点不为val ：执行逻辑是赋值  newhead =tail =  cur; cur = cur->next;  tail->next = NULL;

2) 接下来就是尾插的逻辑，只需要更新尾结点即可  tail ->next = cur; tail = tail->next; cur = cur->next; tail->next = NULL;(注意这2句代码顺序不能颠倒) 

草图见下：

OJ完整代码：

struct ListNode* removeElements(struct ListNode* head, int val)
{    
 //方法2：尾插
    struct ListNode* tail = NULL,*newhead = NULL,*cur = head;
    if(head == NULL)
    return NULL;
    while(cur)
    {
        if(cur->val != val )
        {
            if(newhead == NULL)  //第一次尾插
            {
                newhead = tail =  cur;
                cur = cur->next;
                tail->next = NULL;
            }
            else
            {
                tail->next = cur;
                tail = tail->next;//尾结点更新
                cur = cur->next;
                tail->next = NULL;//注意以上2句代码位置不能颠倒
            }
        }
        else
        {
            struct ListNode* del  = cur;
            cur = cur->next;
            free(del);
        }
    }
    return newhead;
}

2：反转一个单链表

题目：

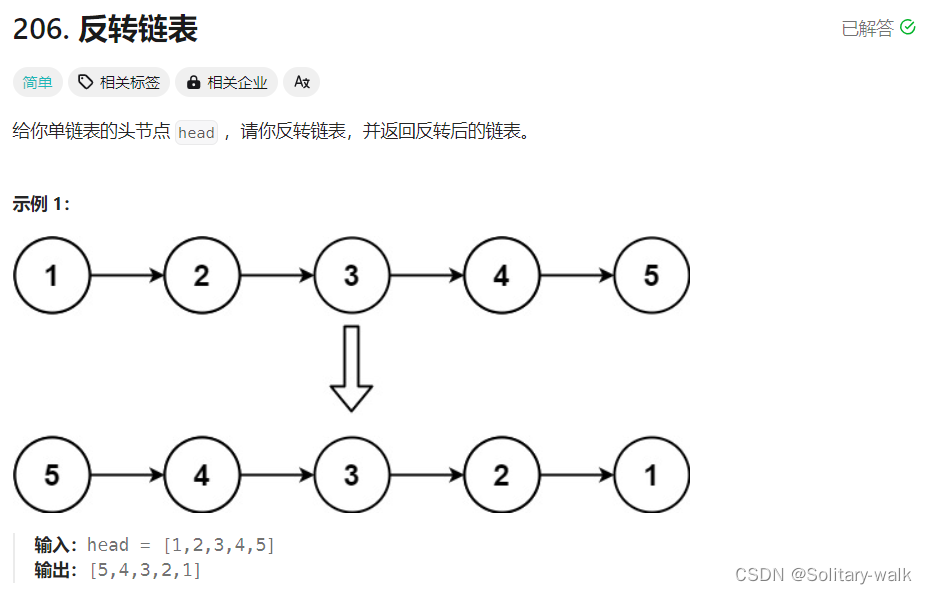
 思路分析

对于这题，咱也就是说，不仅仅局限于一种思维，咱格局打开 

方法1：三指针玩法（说白了，就是改变指针走向的问题）

总的方向：定义三个指针 n1 = NULL ; n2 = head; n3 = head->next ;

注意细节：

1）当链表为空的时候 

n3 = head->next; 这不就出现野指针问题了吗

合理的操作应该是：

if(head == NULL)

    return NULL;

2）循环结束条件的判断： 

3）新的头结点的返回

草图见下：

 OJ代码：

struct ListNode* reverseList(struct ListNode* head) {
    // struct ListNode* n1= NULL,*n2 = head,n3 = n2->next;//可能只有一个节点，此时n3是野指针
struct ListNode* n1= NULL,*n2 = head ;
if(head == NULL)//没有节点
return NULL;
if(head->next == NULL) //只有一个节点
return head;
    struct ListNode*n3 = n2->next;
while(n2)
{
     n2->next = n1;
    n1 = n2;
    n2 = n3;
    if(n3)
    n3 = n3->next;
}
   return n1; 
}

 方法2：利用头插的思想，定义2个指针  newhead = NULL,cur = head;

struct ListNode* reverseList(struct ListNode* head) {
struct ListNode*  newhead = NULL,*cur = head;
if(head == NULL)
return NULL;
while(cur)
{
    struct ListNode * Next = cur->next;//保留cur的下一个节点，避免找不到
    cur->next = newhead;
    newhead = cur;//新的头结点
     cur = Next;
}
return newhead;
}

3：链表的中间结点

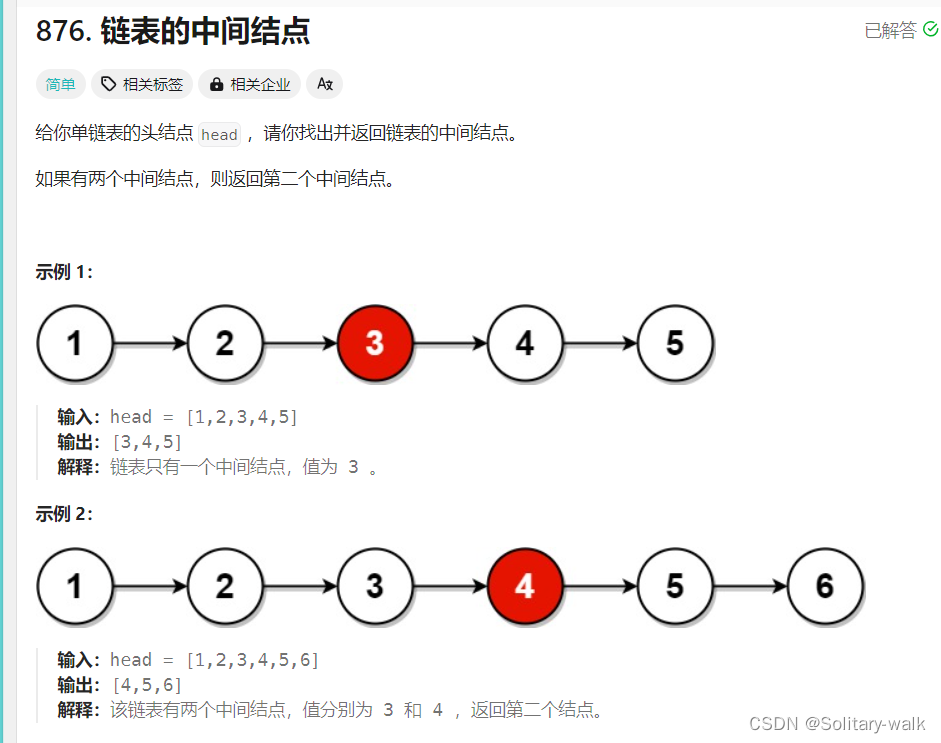
 思路分析

 采用快慢指针（fas指针走2步，slow指针走1步）

原理：在速度上fast永远是slow的2倍，所以当fast走到头的时候slow刚好走到链表的一半，slow所指向的节点就是链表的中间节点

 OJ代码：

struct ListNode* middleNode(struct ListNode* head) 
{
    if(head == NULL)
    return NULL;
    struct ListNode* fast = head,*slow = head;
    while(fast && fast->next)//逻辑必须是且的关系
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

4：链表中倒数第k个结点

题目：

思路讲解： 

方法1：快慢指针（注意这个与上面又有区别只不过思想是一致的） 

1）定义2个指针 fast,slow

2）先让fast指针走k步：利用循环来实现

3）再让2个指针一起走：fast走1步，slow走1步

fast = fast->next->next;

slow = slow->next; 

OJ代码：

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
    // write code here
    struct ListNode* fast = pListHead,*slow = pListHead,*cur = pListHead;
    if(pListHead ==NULL)
    return NULL;
    int count = 0;
    while(cur)//先求出链表长度
    {
        count++;
        cur = cur->next;
    }
    if(k > count || k == 0)
    return NULL;
    while(k--)
    {
        fast = fast->next; 
    }
    while(fast)
    {
        fast = fast->next;
        slow = slow->next;
    }
    return slow;
}

5：合并两个有序链表

题目：

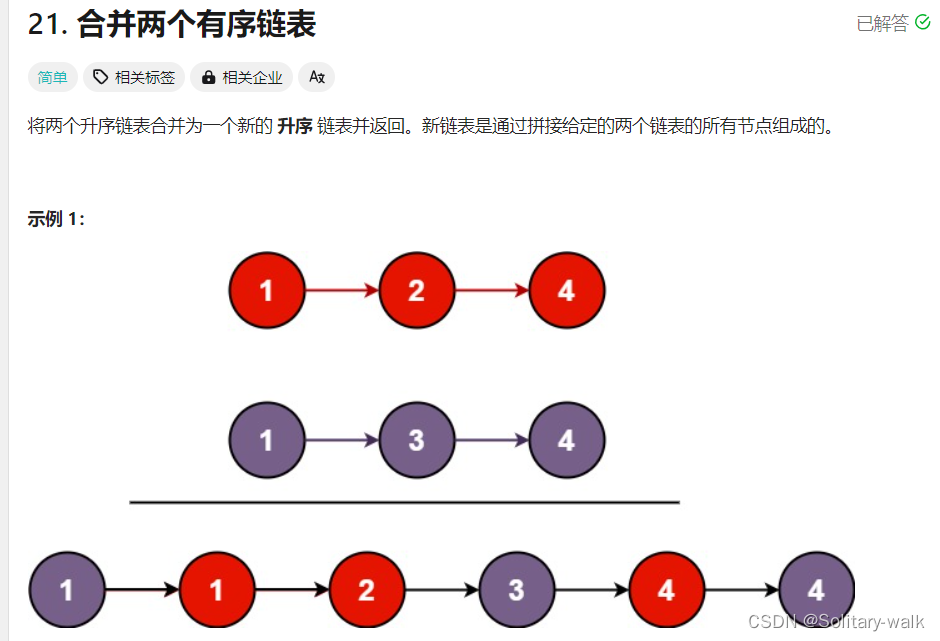
思路分析： 

比较val ，取小的进行尾插

1：定义一个head 指针，一个tail 指针（免去了每一次尾插都需要找尾结点）

2：注意临界条件的判断

草图见下：

OJ代码：

struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
    
    struct ListNode* head = NULL,*tail = NULL;
    if( list1 == NULL&& list2 == NULL)
    return NULL;
    if(list1 == NULL)
    return list2;
    if(list2 == NULL)
    return list1;
    while(list1 && list2 )
    {
        if(list1->val >= list2->val) 
        {
            if(tail == NULL) //第一次尾插
            {
             head = tail= list2;
             list2 = list2->next;
             tail->next = NULL;
            }
            else
            {
             tail->next = list2;
             tail = tail->next;
             if(list2)
              list2 = list2->next;
             tail->next = NULL;//尾结点更新
                
            }
        }
        else
        {
             if(tail == NULL) //第一次尾插
            {
             head = tail= list1;
             list1 = list1->next;
             tail->next = NULL;
            }
            else
            {
            tail->next = list1;
             tail = tail->next;
             if(list1)
            list1 = list1->next;
             tail->next = NULL;//尾结点更新 
            }
        }
    }
    if(list1 != NULL)
    {
        tail->next = list1;
    }
    if(list2 != NULL)
    {
        tail->next = list2;
    }
    return head;
}

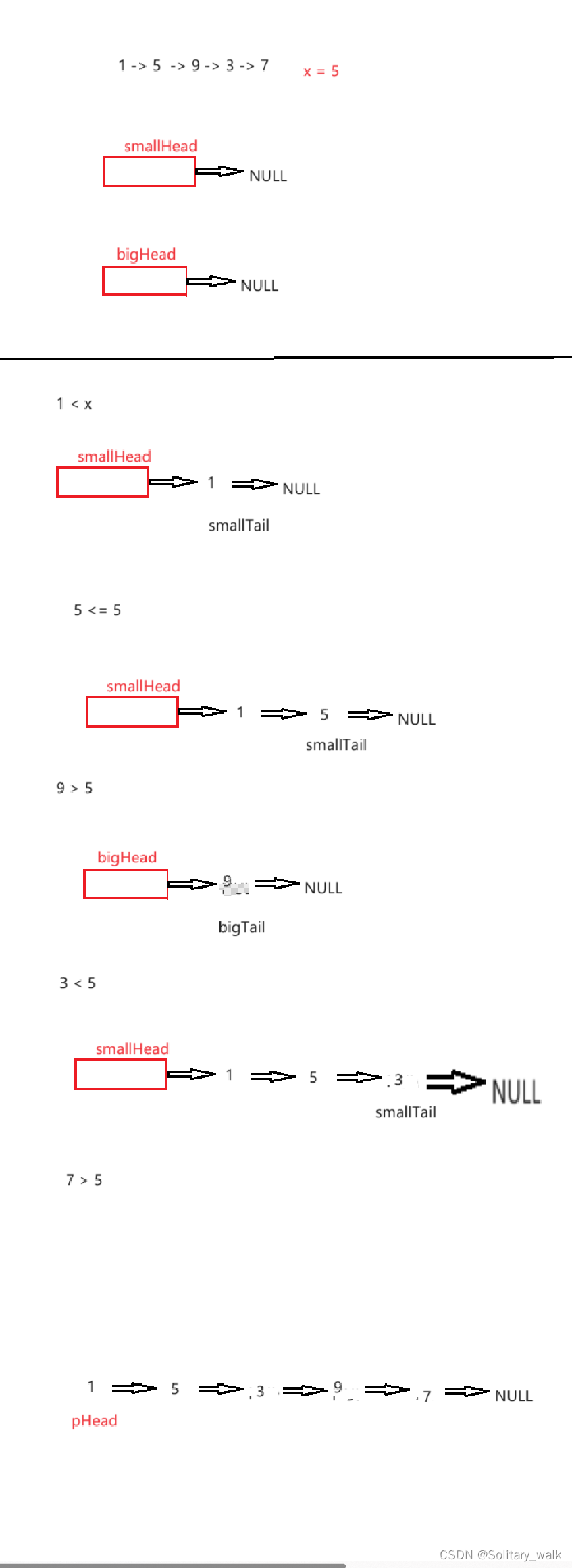
6：链表分割

题目：

 思路分析

首先定义2个哨兵位 ： smallHead (指向小于 x值的对应链表）  bigHead(指向大于 x值的对应链表) 避免了空指针的问题

同时方便我们尾插进来找尾结点 定义2个尾指针 smallTail   bigTail

小于 x 进行尾插在 smallTail 

大于 x进行尾插在bigTail

最后把 2个链表进行连接

 草图见下

OJ代码

class Partition {
public:
ListNode* partition(struct ListNode* pHead, int x)
{
    // write code here
    /*
    思路：这两个链表一定要带哨兵位
    小于 x 的尾插到 一个链表
    大于等于 X 的尾插到另一个链表上
    对尾插的节点进行连接
     */
    struct ListNode* smallHead = nullptr, * smallTail = nullptr, * bigHead = nullptr, * bigTail = nullptr;//定义2个哨兵位
    struct ListNode* cur = pHead;
    smallHead = (struct ListNode*)malloc(sizeof(struct ListNode));
    bigHead = (struct ListNode*)malloc(sizeof(struct ListNode));
    smallHead->next = nullptr;
    smallHead->val = -1;
    bigHead->val = -1;
    bigHead->next = nullptr;
    while (cur)
    {
        if (cur->val next;
                smallTail->next = nullptr;
                smallHead->next = smallTail;
            }
            else
            {
                smallTail->next = cur;
                cur = cur->next;
                smallTail = smallTail->next;
                smallTail->next = nullptr;
                // cur = cur->next;
            }
        }
        else
        {
            if (bigTail == nullptr)
            {
                bigTail = cur;
                cur = cur->next; NULL;
                bigHead->next = bigTail;
            }
            else
            {
                bigTail->next = cur;
                cur = cur->next;
                bigTail = bigTail->next;
                bigTail->next = nullptr;
            }
        }
    }
    //小的链表尾连接到大的链表的头
    if (smallTail)
    {
        smallTail->next = bigHead->next;
        pHead = smallHead->next;
    }
    else
    {
        pHead = bigHead->next;//smallTail可能为空
    }
    //把2个哨兵位释放
    free(smallHead);
    free(bigHead);
    return pHead;
}
};

7：链表的回文结构

题目：

思路分析：

大方向： 中间节点 + 链表逆置

1：先找到链表的中间节点 

注意：链表有偶数个节点返回第二个节点

1-> 2-> 2-> 1  对应的中间节点：就是倒数倒数第二个节点

1-> 2-> 3        对应中间节点：就是第二个节点

对于这个代码逻辑的分析，就借助题目3实现即可

链表逆置代码逻辑的分析见题目2

说实话，有的时候 "CV" 大法对于我们程序员来说还是挺香滴

有时候在修修改改，就OK

OJ代码：

class PalindromeList {
public:
struct ListNode* middleNode(struct ListNode* head) //返回链表中间节点
{
    if(head == nullptr)
    return nullptr;
    struct ListNode* fast = head,*slow = head;
    while(fast && fast->next)//逻辑必须是且的关系
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}
struct ListNode* reverseList(struct ListNode* head) //链表逆置
{
struct ListNode*  newhead = nullptr,*cur = head;
if(head == nullptr)
return nullptr;
while(cur)
{
    struct ListNode * Next = cur->next;//保留cur的下一个节点，避免找不到
    cur->next = newhead;
    newhead = cur;//新的头结点
     cur = Next;
}
return newhead;
}
    bool chkPalindrome(ListNode* head) {
        // write code here
        // 找到中间节点（偶数个节点：返回第二个）；从中间节点开始进行逆置；以此判断val
       struct ListNode * mid =  middleNode( head);
       struct ListNode * re_mid = reverseList(head);
       while(head)
       {
        if(head->val != re_mid->val)
        {
            return false;
        }
        else {
        head = head->next;
        re_mid =  re_mid->next;
        }
       }
       return true;
    }
};

8：相交链表

 题目：

对于这个OJ题，可能大部分老铁是这样想的：

对这2个链表的每个节点依次进行比较，看链表A 中的 a1是否与链表B中的某个节点相等。搞个循环就拿下了，不知道你是否思考过时间复杂度 ：这个时间复杂度对应的级别O(N^2），在OJ上是跑不过去的

 思路分析：

若是2个链表的尾结点相同，岂不是就相交了

1：注意这里不能比较 节点的val是否相同（此时尾结点的val一样，但是不相交）

2：借用快慢指针的思想：定义fast (指向较长的一个链表)slow(指向链表较短的一个)

3：先让fast走绝对值步 abs(lA-lB)  :注意abs（）是一个库函数

4：在让 fast  和 slow 各自走一步进行判断是否  fast == slow

5：注意一些细节处理：2个链表只有一个节点；当2个链表的长度差很大（换言之就是：slow很快就来到尾结点）

6：找链表尾结点 是 tail ->next == NULL(而不是 tail == NULL)

7:判断链表哪一个长，可以定义一个 longListNode, shortListNode，指针含义顾名思义，这样就避免了每次进循环后的重复判断

 草图见下：

 OJ代码：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    /*
    快慢指针（拉开距离）：fast（指向较长的链表）slow（指向较短链表）一起走，每次走一步，第一次 fast == slow,就是所求节点
    fast先走 差距步  abs(lA-lB)
    问题不知道那个链表是最长的，定义指针 shortList,longList
    */
    struct ListNode * tailA = headA,*tailB = headB;
   
    int lA = 0,lB = 0;
    while( tailA->next)
    {
        lA++;//注意lA最终比原链表长度少1，但并不影响 abs(lA-lB)
        tailA = tailA->next;
    }
    while(tailB->next)
    {
        lB++;
        tailB = tailB->next;
    }
    int gap = abs(lA-lB);
    if(tailB == tailA)  //相交
    {
        struct ListNode* longList= headA,*shortList = headB;//假设链表A较长
        if(lA >= lB)
        {
        longList = headA;
        shortList = headB;
        }
        else
        {
        longList = headB;
        shortList = headA;
        }
        struct ListNode*fast = longList,*slow = shortList;
        while(gap--)
        {
            fast = fast->next;
        }
        //都只有一个节点，下面循环进不去
        if(fast == slow)
        return fast;
        while(fast && fast->next)
        {
            fast = fast->next;
            if(slow != NULL)  //可能slow先来到尾结点
            slow = slow->next;
            if(fast == slow)
            return fast;
        
        }
    }
    return NULL;//不相交
}

9： 环形链表

题目：

注意此时我们找尾结点是不能解决问题的

对于这种循环链表最大的问题就是不能进行遍历，因为我们永远走不出这个圈（一直死循环） 

 思路分析：

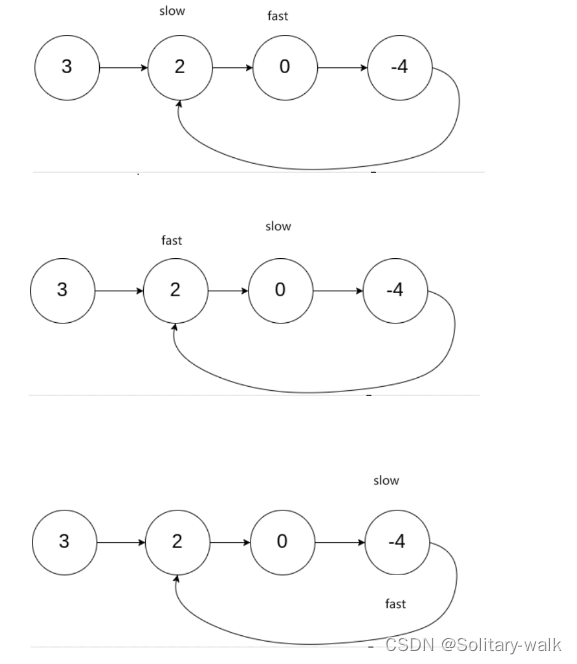
方法：快慢指针

1：fast 和 slow 起始位置都指向头结点

2：fast 每次走 2步  fast = fast ->next ->next ;

     slow 每次走一步 slow = slow ->next ;

3: 当这2个指针相遇即代表此链表成环   即： fast == slow  ；

草图分析：

 比如说：屏幕前的老铁，这正好就是面试题之一，面试官就问原理是啥，

fast 和 slow 一定会相遇吗（fast 走2步，slow 走1步）

fast 走3 \4 \5……又可不可以呢？？？

 相信有不少铁子也会有疑问，为什么呀，原理是啥？？？

证明：

fast 每次走2步， slow 每次走一步，并且这2个指针同时从头结点开始走，那么注定fast指针先进入环，slow 指针后进入环

假设fast 指针追 slow 指针，假设fast 与slow 之间距离为 X 。在速度上 fast 是slow 是2倍，并且 2个指针又是同时从统一起始点出发的，所以当slow 第一次进入环后但没有走完第一圈，fast 肯定会追上 slow

OJ代码：

bool hasCycle(struct ListNode *head)
 {
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        return true;
    }
    return false;
}

10：环形链表 II

 题目：

对于这个变形题，咱先说思路，一会在进行证明 

思路分析：

方法：一个指针从头结点开始走，一个指针从相遇的节点开始走，当再次相遇即为环的入口节点（即为所求）

 1：快慢指针的思想：当 fast 和 slow 第一次相遇的时候 定义为 meet

2：有一个指针从头结点开始走，一个指针从meet 这个节点开始走，当这2个指针再次相遇即为链表成环的第一个节点

再则里，俺就偷个懒，就不画草图喽

OJ代码： 

struct ListNode *detectCycle(struct ListNode *head) 
{
    /*
    1:判断是否有环：快慢指针
    2：求入环的起始节点->假设相遇的节点是meet，让一个节点从meet开始走，一个从头结点开始走，再次相遇即为所求
    */
    struct ListNode * fast = head,*slow =  head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if( slow == fast)//相遇
        {
            struct ListNode * meet = slow;
            while(meet != head)
            {
                meet = meet->next;
                head = head->next;
            }
                return meet;
            
        }
    }
    return NULL;//没有环
}

 想必有不少老铁会问，原理是啥，能对这个结论进行证明吗？

没问题，接下来3,2,1，上证明

证明：

11：随机链表的复制

题目：

分析： 

当我们看到这个链表的时候，无非就是多了一个 random 指针相较于 单链表而言

我相信有不少老铁是这样思考的：

当节点的random 指针指向非空的时候：第二个节点 直接让 random 指向 节点val 为 7的节点即可

我在这里想说是不行滴当链表LI有2个为7的节点呢，你知道先连哪一个吗？

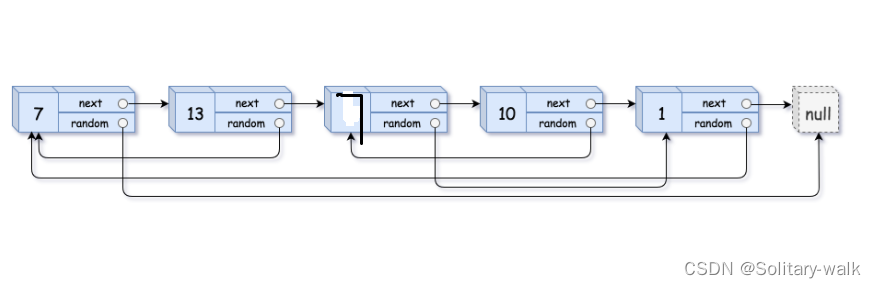
 有那些铁子说：不如记录一下当前 random 指针指向第几个节点

这样也不是不可以的，但是效率肯定是不太好的 O(N^2)

 我这里有个最优解（仅限于使用C语言）仔细看哟，不要分心，一不小心就出差错了

额外说一下：此时对应时间复杂度的级别是 O（N）

思路分析：

首先：对原来链表进行拷贝，让原节点与拷贝节点建立联系：拷贝的节点尾插到对应节点的后面

其次：控制拷贝节点的random   注意这是解这题的核心

     当random 不为空：  copy -> random = cur ->random->next ;

     当random 为空：copy ->random = NULL ;

最后：让拷贝链表与原链表分开，同时恢复原来链表

定义 3个指针：

copyHead （拷贝链表新的头结点）  copyTail（拷贝链表的尾结点）    curNext

1）把拷贝节点拿下来尾插

对拷贝节点第一次尾插

            copyHead = copyTail = cur -> next ;

            curNext = cur->next->next;

            cur->next = curNext;//恢复原来链表

            cur = curNext;

            copyTail ->next = NULL;

之后对拷贝节点尾插逻辑：

            copyTail->next =cur->next;

            curNext = cur->next->next;

            cur ->next = curNext;//恢复原来链表

            cur = curNext;//迭代

            copyTail = copyTail->next;//尾结点及时更新

            copyTail ->next = NULL;//尾结点及时置空

2）原链表的恢复：让cur -> next = curNext ;

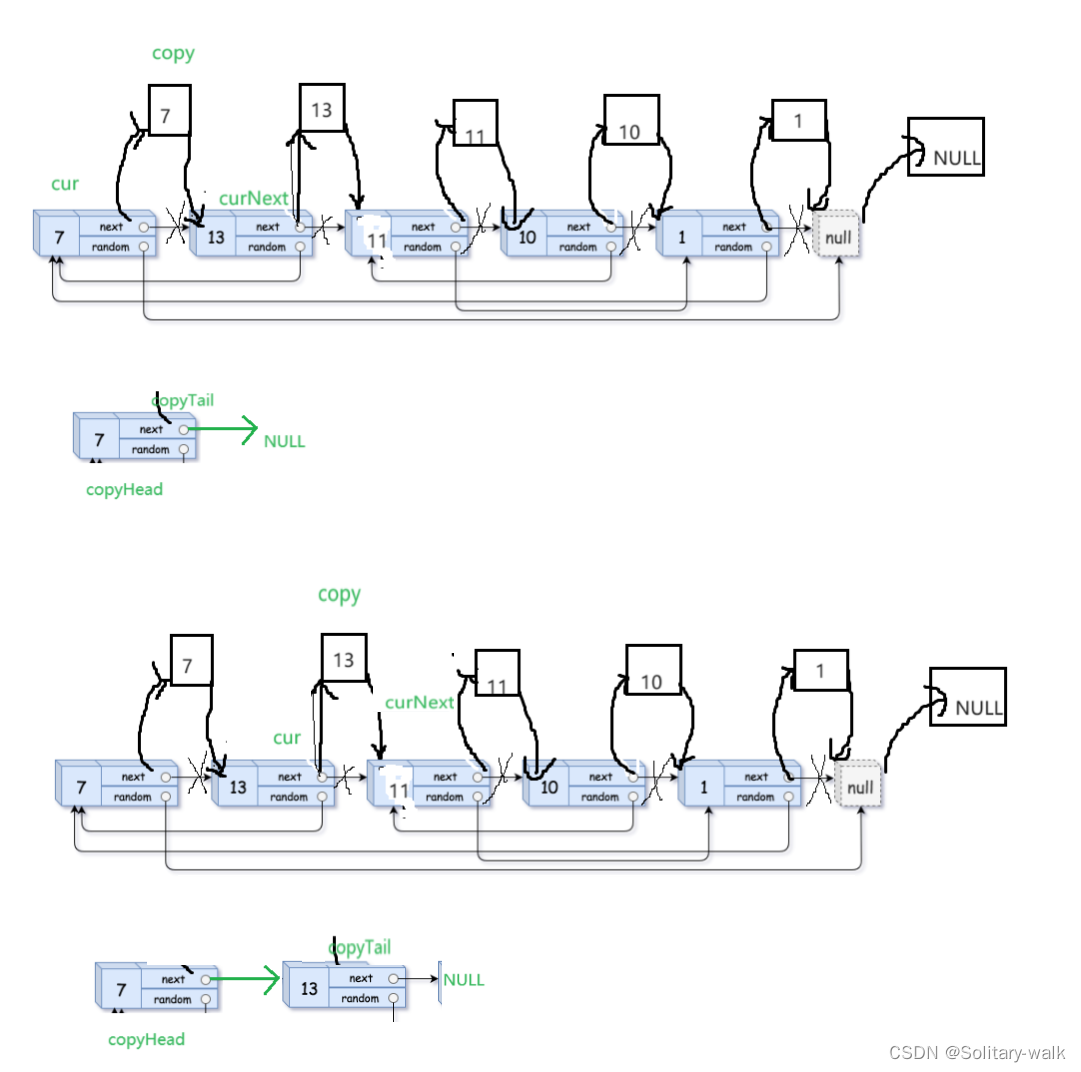
 OJ代码：

struct Node* copyRandomList(struct Node* head)
 {
     /*
     1:拷贝节点到原来节点的后面：是源节点与拷贝节点建立联系（实际上：没有任何关系：malloc）
     2：控制拷贝节点的random
     3：让拷贝节点与源节点断开 && 恢复原来链表
     */
	struct Node* cur = head,*copy = NULL;
    while(cur) //1
    {
        copy = (struct Node*)malloc(sizeof(struct Node));
        if(copy == NULL)
        return NULL;
        //开辟成功，赋值
        copy->val = cur->val;
        copy->next = cur->next;
        struct Node* curNext = cur->next;
        //插入到当前节点后面
        cur->next = copy;
        copy->next = curNext;
        cur = curNext;//迭代
    }
    cur = head;//cur重新赋值
    // copy = cur->next;
    while(cur)//2
    {
         copy = cur->next;//拷贝节点永远在cur 的后面
        if(cur->random == NULL)
        {
             copy->random = NULL;
        }
        else
        {
        copy->random = cur->random->next;
        }
        cur = copy->next;//迭代
    }
    cur = head;//cur重新赋值
    struct Node* copyHead = NULL,*copyTail = NULL,*curNext = NULL;
    while(cur)//3:把拷贝节点取下来尾插
    {
        if(copyTail ==NULL)
        {
            copyHead = copyTail = cur->next;
            curNext = cur->next->next;
            cur->next = curNext;//恢复原来链表
            cur = curNext;
            copyTail ->next = NULL;
        }
        else
        {
            copyTail->next =cur->next;
            curNext = cur->next->next;
            cur ->next = curNext;//恢复原来链表
            cur = curNext;//迭代
            copyTail = copyTail->next;//尾结点及时更新
            copyTail ->next = NULL;//尾结点及时置空
        }
    }
    return copyHead;
}

总结： 

对于我这种小白来讲，做链表方面的OJ题，结合画图来说确实是省了不少事情，相比较自己 盲想省去了不少麻烦，在之后就是自己还是要多多练习，注意指针走向，边界的判断

结语：

对于链表这块，需要咱们多多实践，这样才能知不足，而奋进。对于这个快慢指针的应用我们方向是很灵活的，有时候看似题目很难（比如求环形链表入口的第一个节点），采用快慢指针代码量瞬间就变得很精简。其次就是我们在敲代码的时候要注意“数码结合”，画图真的帮我们省了不少问题，ok，话不多说，咱走起，你是懂滴，铁子！