算法沉淀——BFS 解决 FloodFill 算法（leetcode真题剖析）

算法沉淀——BFS 解决 FloodFill 算法

• 01.图像渲染
• 02.岛屿数量
• 03.岛屿的最大面积
• 04.被围绕的区域

  BFS（广度优先搜索）解决 Flood Fill 算法的基本思想是通过从起始点开始，逐层向外扩展，访问所有与起始点相连且具有相同特性（颜色等）的区域。在 Flood Fill 中，通常是通过修改图像的像素颜色。

  下面是 BFS 解决 Flood Fill 算法的步骤：

  1. 初始化： 将起始点的颜色修改为新的颜色，将起始点加入队列。
  2. BFS 遍历： 使用队列进行 BFS 遍历。每次从队列中取出一个位置，检查其相邻的位置是否符合条件（与起始点颜色相同），如果符合，则修改颜色并将其加入队列。这样，不断扩展遍历。
  3. 遍历直到完成： 重复上述步骤，直到队列为空，即没有可继续扩展的位置为止。此时，所有与起始点相连的区域都被成功修改。

  在 Flood Fill 中，BFS 保证了相邻区域的逐层遍历，确保了所有相连的、颜色相同的区域都被填充为新的颜色。

  01.图像渲染

  题目链接：https://leetcode.cn/problems/flood-fill/

  有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。

  你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。

  为了完成 上色工作 ，从初始像素开始，记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为 newColor 。

  最后返回 经过上色渲染后的图像 。

  示例 1:

  

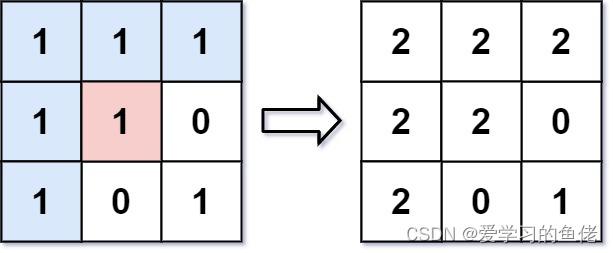
  输入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2
  输出: [[2,2,2],[2,2,0],[2,0,1]]
  解析: 在图像的正中间，(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。
  注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。
  

  示例 2:

  输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
  输出: [[2,2,2],[2,2,2]]
  

  思路

  这个题我们可以使用最朴素的bfs遍历来解决。

  代码

  class Solution {
      const int dx[4] = {0, 0, 1, -1};  // 表示上、下、左、右四个方向的相对坐标变化
      const int dy[4] = {-1, 1, 0, 0};
  public:
      vector floodFill(vector& image, int sr, int sc, int color) {
          int prev = image[sr][sc];  // 记录起始位置的颜色
          if (prev == color) return image;  // 如果新旧颜色相同，不需要进行填充
          int m = image.size(), n = image[0].size();
          queue q;
          q.push({sr, sc});
          while (!q.empty()) {
              auto [a, b] = q.front();
              q.pop();
              image[a][b] = color;  // 修改当前位置的颜色
              for (int i = 0; i = 0 && x = 0 && y  
  初始化： 记录起始位置的颜色 prev，如果起始颜色和目标颜色相同，直接返回原图。
  BFS 遍历： 使用队列 q 进行 BFS 遍历。从起始位置开始，逐层遍历相邻位置，将颜色修改为目标颜色。
  遍历直到完成： 重复上述步骤，直到队列为空，即没有可继续扩展的位置为止。此时，所有与起始点相连的区域都被成功修改为新的颜色。
  02.岛屿数量
   
  题目链接：https://leetcode.cn/problems/number-of-islands/
   
  给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。
   
  岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
   
  此外，你可以假设该网格的四条边均被水包围。
   
  示例 1：
   
  输入：grid = [
    ["1","1","1","1","0"],
    ["1","1","0","1","0"],
    ["1","1","0","0","0"],
    ["0","0","0","0","0"]
  ]
  输出：1
   
  示例 2：
   
  输入：grid = [
    ["1","1","0","0","0"],
    ["1","1","0","0","0"],
    ["0","0","1","0","0"],
    ["0","0","0","1","1"]
  ]
  输出：3
   
  提示：
   
  

  • m == grid.length
  • n == grid[i].length
  • 1 const int dx[4] = {0, 0, 1, -1}; // 表示上、下、左、右四个方向的相对坐标变化 const int dy[4] = {1, -1, 0, 0}; int m, n; // m表示行数，n表示列数 queue q.push({i, j}); // 将起点入队 grid[i][j] = '0'; // 标记已经遍历过的位置 while (!q.empty()) { auto [a, b] = q.front(); q.pop(); for (int k = 0; k
    1. 初始化： 定义了方向数组 dx 和 dy，表示上、下、左、右四个方向的相对坐标变化。初始化队列 q，用于BFS遍历。
    2. BFS遍历： 对于每个未被访问的岛屿起点，调用 bfs 函数进行BFS遍历。在BFS过程中，将属于同一岛屿的位置标记为已访问。
    3. 遍历整个网格： 使用两层循环遍历整个网格，如果发现未访问过的岛屿起点，就调用 bfs 函数进行遍历，并增加岛屿数量计数。
    4. 返回结果： 最终返回岛屿的数量。

    03.岛屿的最大面积

    给你一个大小为 m x n 的二进制矩阵 grid 。

    岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

    岛屿的面积是岛上值为 1 的单元格的数目。

    计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

    示例 1：

    

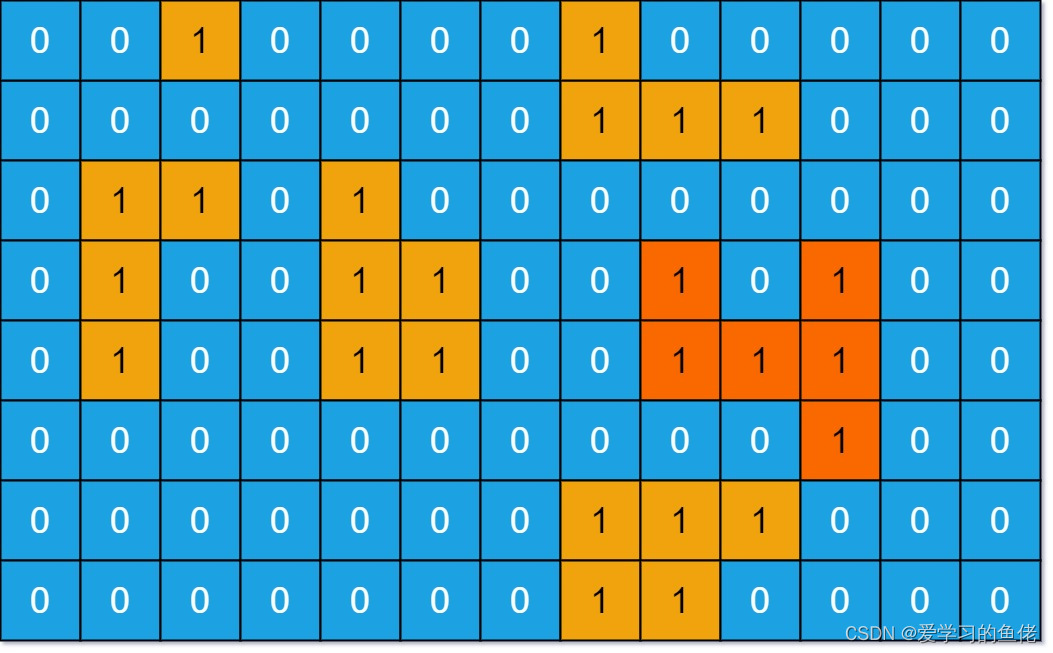
    输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
    输出：6
    解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
    

    示例 2：

    输入：grid = [[0,0,0,0,0,0,0,0]]
    输出：0 
    

    提示：

    • m == grid.length
    • n == grid[i].length
    • 1 const int dx[4] = {0, 0, 1, -1}; // 上、下、右、左四个方向的相对坐标变化 const int dy[4] = {-1, 1, 0, 0}; queue int count = 1; // 记录岛屿的大小 q.push({i, j}); // 将起点入队 grid[i][j] = 0; // 标记已经遍历过的位置 while (!q.empty()) { auto [a, b] = q.front(); q.pop(); for (int k = 0; k
      1. 初始化： 定义了方向数组 dx 和 dy，表示上、下、左、右四个方向的相对坐标变化。初始化队列 q，用于BFS遍历。
      2. BFS遍历： 对于每个未被访问的岛屿起点，调用 bfs 函数进行BFS遍历。在BFS过程中，将属于同一岛屿的位置标记为已访问，并统计岛屿的大小。
      3. 遍历整个网格： 使用两层循环遍历整个网格，如果发现未访问过的岛屿起点，就调用 bfs 函数进行遍历，并计算并更新最大岛屿面积。
      4. 返回结果： 最终返回最大岛屿面积。

      04.被围绕的区域

      题目链接：https://leetcode.cn/problems/surrounded-regions/

      给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

      示例 1：

      

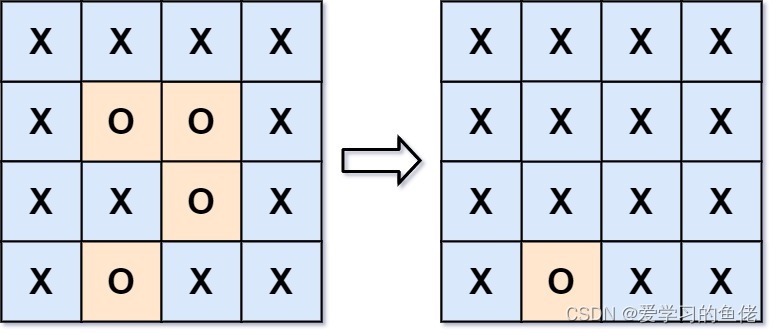
      输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
      输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
      解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。
      

      示例 2：

      输入：board = [["X"]]
      输出：[["X"]]
      

      提示：

      • m == board.length
      • n == board[i].length
      • 1 const int dx[4] = {0, 0, 1, -1}; // 上、下、右、左四个方向的相对坐标变化 const int dy[4] = {-1, 1, 0, 0}; int m, n; // m 表示行数，n 表示列数 queue q.push({i, j}); // 将起点入队 board[i][j] = '#'; // 标记已经遍历过的位置 while (!q.empty()) { auto [a, b] = q.front(); q.pop(); for (int k = 0; k