C#，数值计算，矩阵的行列式（Determinant）、伴随矩阵（Adjoint）与逆矩阵（Inverse）的算法与源代码

本文发布矩阵（Matrix）的一些初级算法。

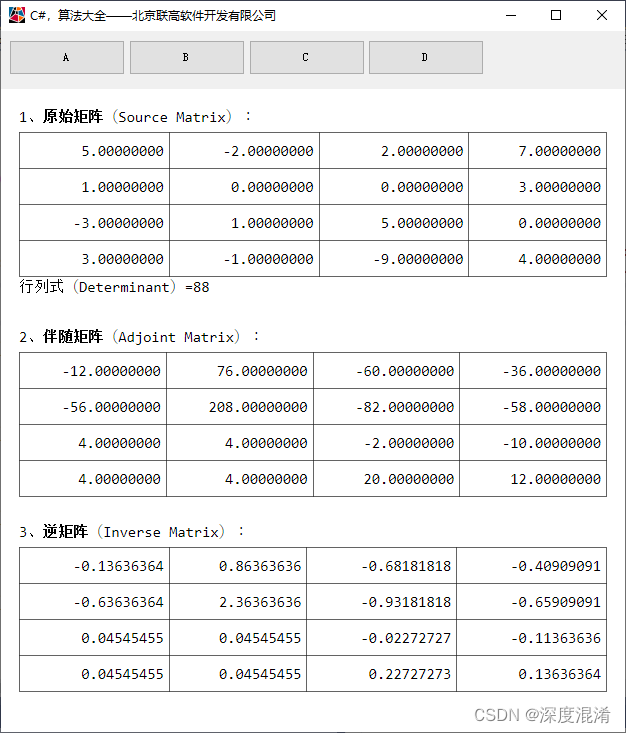
一、矩阵的行列式（Determinant）

矩阵行列式是指矩阵的全部元素构成的行列式，设A=(a)是数域P上的一个n阶矩阵，则所有A=(a)中的元素组成的行列式称为矩阵A的行列式，记为|A|或det(A)。若A，B是数域P上的两个n阶矩阵，k是P中的任一个数，则|AB|=|A||B|，|kA|=kⁿ|A|，|A*|=|A|，其中A*是A的伴随矩阵；若A是可逆矩阵，则|A|=|A|。
 

///
/// 计算 A[p,q] 位于 [,]temp 的块辅因子
///
///
///
///
///
///
private statiC void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n)
{
    int i = 0;
    int j = 0;

    for (int row = 0; row     {
        for (int col = 0; col         {
            if (row != p && col != q)
            {
                temp[i, j++] = matrix[row, col];
                if (j == (n - 1))
                {
                    j = 0;
                    i++;
                }
            }
        }
    }
}

///
/// 求矩阵行列式（递归算法）
///
///
///
///
///
public static double Determinant(int N, double[,] matrix, int n)
{
    if (n == 1)
    {
        return matrix[0, 0];
    }

    double D = 0.0;
    double[,] temp = new double[N, N];
    int sign = 1;
    for (int f = 0; f     {
        BlockCofactor(matrix, ref temp, 0, f, n);
        D += sign * matrix[0, f] * Determinan