力扣编程题算法初阶之双指针算法+代码分析

目录

第一题：复写零

第二题：快乐数：

第三题：盛水最多的容器

第四题：有效三角形的个数

第一题：复写零

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

思路：

上期介绍到双指针，这次来用双指针实际操作。第一种从前往后复写，会导致为复写的数字被覆盖，因此选择从后往前复写，那么先找到复写的最后一个元素，再从后往前复写即可。

步骤

1.初始化指针

2.找复写

3.处理边界问题

4.开始复写

class Solution {
public:
    void duplicateZeros(vector& arr) {
        	int cur = 0, dest = -1, n = arr.size();
while (cur = n - 1)break;
	cur++;
}
//出来的时候cur就是莫位置
//处理边界
if (dest == n)
{
	arr[n - 1] = 0;
	cur--; dest -= 2;
}
//从后往前面复写
while (cur >= 0)
{
	if (arr[cur])//非0
		arr[dest--] = arr[cur--];
	else//为0
	{
		arr[dest--] = 0;
		arr[dest--] = 0;
		cur--;
	}
}
    }
};

第二题：快乐数：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

思路：

这题通过在纸上演算可以发现，给定一个数他按照快乐数的定义，要么演变到1，要么将会重复他在演变过程中的一个数字，具体大家可以在纸上推算一遍

即

： 1.先把n的每一位提出，直到n为0 2.接着只要两个指针不相等就一直重复快乐数定义，直到相等退出循环，判断是否为1

class Solution
{
public:
	int bitSum(int n)
		int sum = 0;
	while (n)
	{
		int t = n % 10;
		sum += t * t;
		n /= 10;
	}
	bool isHappy(int n)
	{
		int slow = n, fast = bitSum(n);
		while (slow != fast)
		{
			slow = bitSum(slow);
			fast = bitSum(bitSum(fast));
		}
		return slow == 1;
	}
};

第三题：盛水最多的容器

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

思路：

第一想法就是暴力枚举

s=h（高）*w（宽度）

即弄两个for循环，依次求出面积，再比较最大值，这样时间复杂度为n的平方会超时，因此

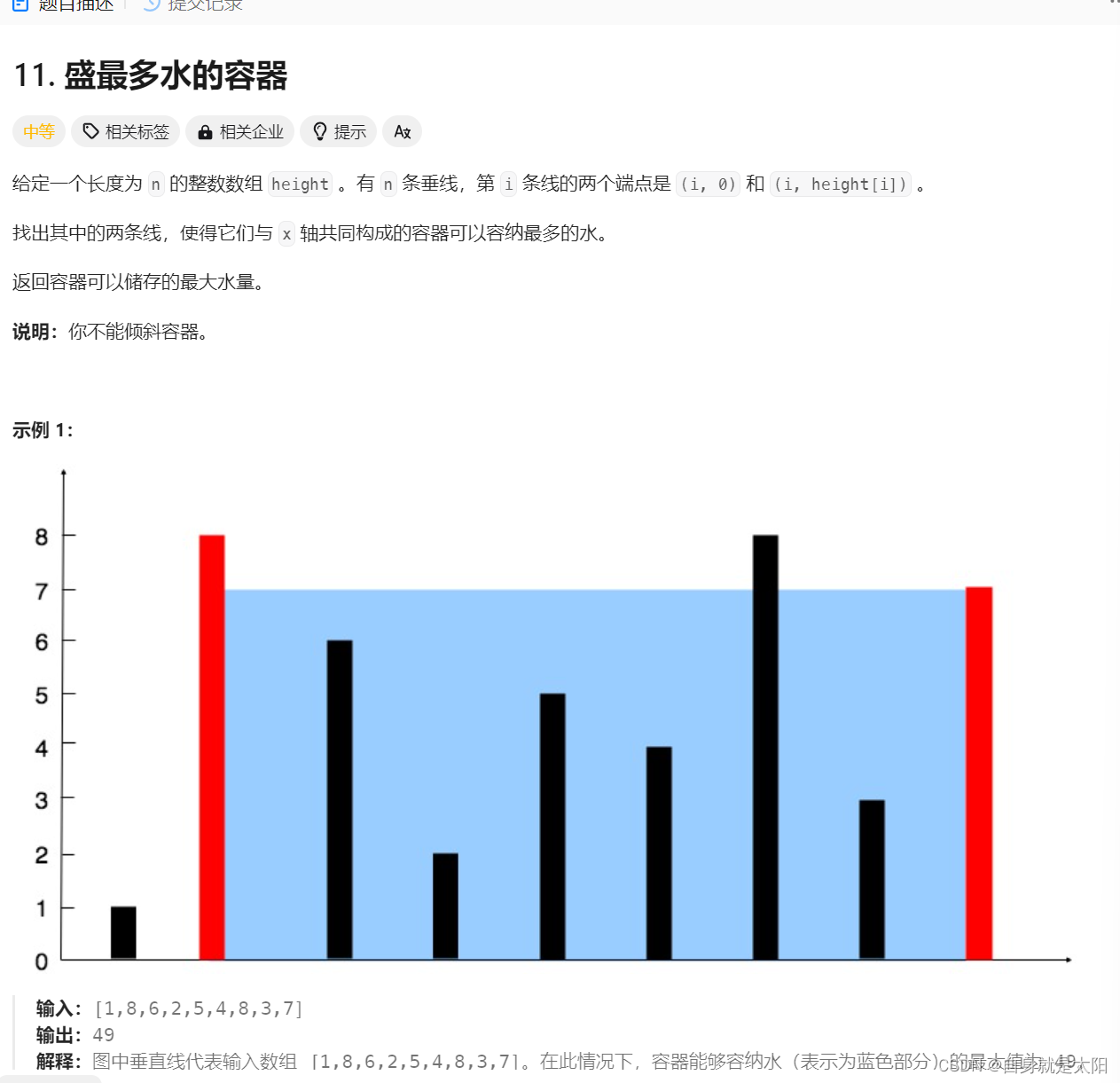
第二种就是双指针，观察发现，面积的高是由左右两边的低边界为准。就以上图为例，高是由右边那条高决定，左边高往右移动由于w一定减小，h要么减小要么不变，那么面积一定减小，所以我们就从两个边界开始来移动，记录每一次的面积，返回最大即可

注意，每次移动的是那个h小的，因为大h移动，s要么减少要么不变，而我们求的是最大的。

第一种：暴力求解

class Solution {
public:
	int maxArea(vector& height) {
		int n = height.size();
		int ret = 0;
		// 两层 for 枚举出所有可能出现的情况
		for (int i = 0; i  
 
第二种：
 
 
对撞指针：
 
 
class Solution
{
public:
	int maxArea(vector& height)
	{
		int left = 0, right = height.size() - 1, ret = 0;
		while (left  
 
第四题：有效三角形的个数
 
 
力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
 
 
思路：
 
 
在判断一个三角形时，如果对于一对升序数组a,b,c
 
 
如果a+b>c那么即可构成三角形，不需要判断三次
 
 
原因，如果上述条件成立那么，b+c>a,a+c>b一定成立，因为c是最大的数
 
 
第一思路就是暴力求解，先把给定数组排序，然后从第一个元素开始遍历，用三个for循环实现，但是时间复杂度较大，运行会超时
 
 
class Solution {
public:
	int triangleNumber(vector& nums) {
		// 1. 排序
		sort(nums.begin(), nums.end());
		int n = nums.size(), ret = 0;
		// 2. 从⼩到⼤枚举所有的三元组
		for (int i = 0; i  nums[k])
						ret++;
				}
			}
		}
		return ret;
	}
};
 
 
应次这里换一种高效方法就是用双指针来实现，因为已经排完升序，依据暴力解法，可以先固定一条最长边，然后找出比这条边小的二元组，让着个二元组的和大于最长边，即可利用对撞指针来实现。
 
 
   最长边枚举i位置，区间[left,right]是i位置左边区间， 
  
 
   如果nums[left]+nums[right]>num[i]，那么就有right-left种，因为是升序 
  
 
   否则，那么就舍弃left当前元素，left++进入下一轮循环 
  
  
  
class Solution
{
public:
	int triangleNumber(vector& nums)
	{
		// 1. 优化
		sort(nums.begin(), nums.end());
		// 2. 利⽤双指针解决问题
		int ret = 0, n = nums.size();
		for (int i = n - 1; i >= 2; i--) // 先固定最⼤的数
		{
			// 利⽤双指针快速统计符合要求的三元组的个数
			int left = 0, right = i - 1;
			while (left  nums[i])
				{
					ret += right - left;
					right--;
				}
				else
				{
					left++;
				}
			}
		}
		return ret;
	}
};