很多朋友都问我学完基础知识以后怎样提高编程水平?当然是刷题啦!很多小伙伴都在纠结从哪里开始,今天给大家推荐一个身边朋友都在使用的刷题网站:点击进入牛客网刷题吧!

今天是 Java + 经典算法 进阶刷题的第四天,结合经典算法学习Java语法!一起升级打怪吧!!
文章目录
- 问题1:判断是不是二叉搜索树
- 问题2:判断是不是完全二叉树
- 问题3:判断是不是平衡二叉树
- 问题4:二叉搜索树的最近公共祖先
- 问题5:序列化二叉树
- 总结(刷题经验分享)

最近一直在练习二叉树的经典题目。为了巩固基础算法能力,同时也为了在面试中可以做到心中有数,我通过做题的方式让自己头脑保持清醒,让自己对基础算法题目时刻保持感觉。
我几乎每天都通过刷题的方式让自己保持清醒,最近也感觉自己算法能力又明显的提升,所以说,这样的方式是可行的!希望我的刷题笔记能够帮助到大家,接下来让我们一起开始算法之旅吧。
问题1:判断是不是二叉搜索树
原题点击:判断是不是二叉搜索树
题目描述:
给定一个二叉树根节点,请你判断这棵树是不是二叉搜索树。
二叉搜索树满足每个节点的左子树上的所有节点均小于当前节点且右子树上的所有节点均大于当前节点。
例:
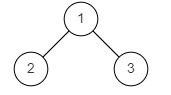
图1
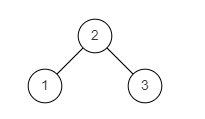
图2
数据范围:
节点数量满足 1 ≤n≤ 10^4
节点上的值满足:
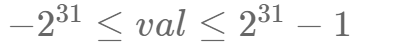
示例1:
输入: {1,2,3}
返回值: false
说明:如题面图1
示例2:
输入: {2,1,3}
返回值: true
说明:如题面图2
题解:
Java代码实现:
import java.util.*; public class Solution { int pre = Integer.MIN_VALUE; //中序遍历 public boolean isValidBST (TreeNode root) { if (root == null) return true; //先进入左子树 if(!isValidBST(root.left)) return false; if(root.val思路: 二叉搜索树的特性就是中序遍历是递增序。既然是判断是否是二叉搜索树,那我们可以使用中序递归遍历。只要之前的节点是二叉树搜索树,那么如果当前的节点小于上一个节点值那么就可以向下判断。
只不过在过程中我们要求反退出。比如一个链表1->2->3->4,只要for循环遍历如果中间有不是递增的直接返回false即可。
if(root.val
问题2:判断是不是完全二叉树
原题点击:判断是不是完全二叉树
题目描述:
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
数据范围: 节点数满足 1≤n≤100
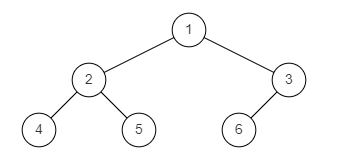
样例图1:
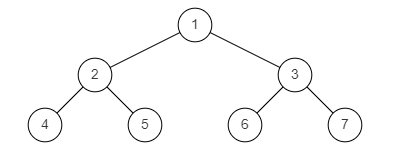
样例图2:
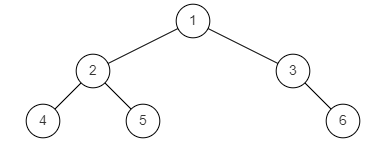
样例图3:
示例1:
输入: {1,2,3,4,5,6}
返回值: true
示例2:
输入: {1,2,3,4,5,6,7}
返回值: true
示例3:
输入: {1,2,3,4,5,#,6}
返回值: false
题解:
Java代码实现:
import java.util.*; public class Solution { public boolean isCompleteTree (TreeNode root) { //空树一定是完全二叉树 if(root == null) return true; //辅助队列 Queue queue = new LinkedList(); queue.offer(root); TreeNode cur; //定义一个首次出现的标记位 boolean notComplete = false; while(!queue.isEmpty()){ cur = queue.poll(); //标记第一次遇到空节点 if(cur == null){ notComplete = true; continue; } //后续访问已经遇到空节点了,说明经过了叶子 if(notComplete) return false; queue.offer(cur.left); queue.offer(cur.right); } return true; } }思路: 对完全二叉树最重要的定义就是叶子节点只能出现在最下层和次下层,所以我们想到可以使用队列辅助进行层次遍历——从上到下遍历所有层,每层从左到右,只有次下层和最下层才有叶子节点,其他层出现叶子节点就意味着不是完全二叉树。
问题3:判断是不是平衡二叉树
原题点击:判断是不是平衡二叉树
题目描述:
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树。
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
样例解释:
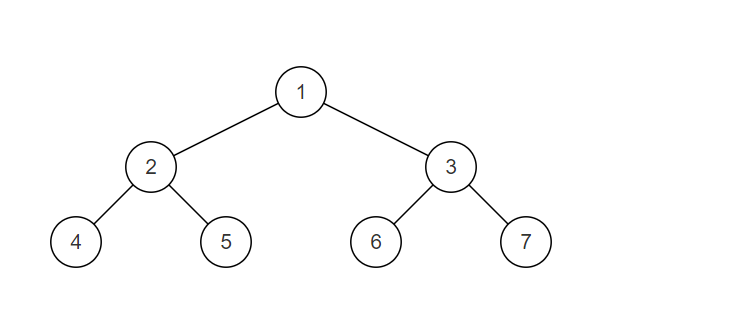
样例二叉树如图,为一颗平衡二叉树
注:我们约定空树是平衡二叉树。
数据范围:n≤100,树上节点的val值满足 0≤n≤1000
要求:空间复杂度O(1),时间复杂度 O(n)
输入描述:
输入一棵二叉树的根节点
返回值描述:
输出一个布尔类型的值
示例1:
输入: {1,2,3,4,5,6,7}
返回值: true
示例2:
输入: {}
返回值: true
题解:
Java代码实现:
public class Solution { //计算该子树深度函数 public int deep(TreeNode root){ //空节点深度为0 if(root == null) return 0; //递归算左右子树的深度 int left = deep(root.left); int right = deep(root.right); //子树最大深度加上自己 return (left > right) ? left + 1 : right + 1; } public boolean IsBalanced_Solution(TreeNode root) { //空树为平衡二叉树 if (root == null) return true; int left = deep(root.left); int right = deep(root.right); //左子树深度减去右子树相差绝对值大于1 if(left - right > 1 || left - right思路: 平衡二叉树任意节点两边的子树深度相差绝对值不会超过1,且每个子树都满足这个条件,那我们可以对每个节点找到两边的深度以后:
int deep(TreeNode root){ if(root == null) return 0; int left = deep(root.left); int right = deep(root.right); //子树最大深度加上自己 return (left > right) ? left + 1 : right + 1; }判断是否两边相差绝对值超过1:
//左子树深度减去右子树相差绝对值大于1 if(left - right > 1 || left - right
然后因为每个子树都满足这个条件,我们还需要遍历二叉树每个节点当成一棵子树进行判断,而对于每个每个节点判断后,其子节点就是子问题,因此可以用递归。
IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
问题4:二叉搜索树的最近公共祖先
原题点击:二叉搜索树的最近公共祖先
题目描述:
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q,最近公共祖先LCA(T,p,q)表示一个节点x,满足x是p和q的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先.
2.二叉搜索树是若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值
3.所有节点的值都是唯一的。
4.p、q 为不同节点且均存在于给定的二叉搜索树中。
数据范围:
3 //求得根节点到目标节点的路径 public ArrayList ArrayList path.add(node.val); //小的在左子树 if(target








