一、时间复杂度(执行的次数)
1.1时间复杂度的概念
1.2时间复杂度的表示方法
1.3算法复杂度的几种情况
1.4简单时间复杂度的计算
例一
例二
例三
1.5复杂时间复杂度的计算
例一:未优化冒泡排序时间复杂度
例二:经过优化的冒泡排序
例三:二分查找的时间复杂度
例四:阶乘递归的时间复杂度
例五:斐波那契递归(二叉树)的时间复杂度
1.6不同时间复杂度效率的比较
编辑
二、空间复杂度(变量的个数)
2.1空间复杂度的概念
2.2常见空间复杂度的计算
对于递归:
前言之空间可以重复利用
例一:冒泡排序的空间复杂度(有坑)
例二:二分法空间复杂度的计算
例三:阶乘递归的空间复杂度
例四:斐波那契递归的空间复杂度(难点)并不是O(2^N)
三、重难点知识回顾与总结
一、时间复杂度(执行的次数)
1.1时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。(这里的函数指的是数学中的函数,而不是我们C语言中的函数)
一个算法执行所耗费的时间,从理论上说是不能算出来的,因为只有当我们把程序放在机器上跑起来,才能知道具体时间。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。
一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
一句话概括:时间复杂度算的是执行次数,而不是具体的时间
但是需要小心误区:并不是有多少个循环次数时间复杂度就是多少,得具体分析算法逻辑
shellsort 用了三个循环 但是它的时间复杂度是O(N^1.3)
1.2时间复杂度的表示方法
我们计算时间复杂度时不是计算算法运行的具体次数,而是用大O的渐进表示法来计算,其具体计算方法如下:
- 用常数1取代运行时间中的所有加法常数。eg:O(100)->O(1)
- 在修改后的运行次数函数中,只保留最高阶项。eg:O(N^2+N)->O(N^2)
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。O(2N^2)->O(N^2)

1.3算法复杂度的几种情况
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
但是需要注意的是:


在实际中一般情况关注的是算法的最坏运行情况
1.4简单时间复杂度的计算
例一
void Func(int N) { int count = 0; for (int k = 0; kO(100)-> O(1)
例二
void Func1(int N) { int count = 0; for (int i = 0; i上面程序具体执行的次数:N * N + 2*N + 10
用大O的渐进表示法得出时间复杂度:O(N^2) (只保留最高阶项)
例三
void Func2(int N) { int count = 0; for (int k = 0; k上面程序具体执行的次数:2*N + 10
用大O的渐进表示法得出时间复杂度:O(N) (如果最高阶项存在且不是1,则去除与这个项目相乘的常数
1.5复杂时间复杂度的计算
例一:未优化冒泡排序时间复杂度
void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { for (size_t i = 1; i a[i]) { Swap(&a[i-1], &a[i]); Exchange = 1; } } } }
分析可知:

所以本质上是一个等差数列
刚开始一共有N个数,所以需要比较N-1次 第二次需要比较 N-2 次
所以(N-1)+(N-2)+(N-3)+...+3+2+1= (N^2-N)/2
用大O的渐进表示法得出时间复杂度:O(N^2)
但是这是未经过优化的冒泡排序,不管原先数组是否有序,都要经过全部遍历
例二:经过优化的冒泡排序
void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i a[i]) { Swap(&a[i-1], &a[i]); exchange = 1; } } if (exchange == 0) { break; } } }多了一个exchange变量,这个变量的好处是:
对于已经有序的数组,不再会进行排序
当exchange为0时,表示在当前一轮的比较中没有发生任何元素交换,这意味着待排序的数组已经是有序的状态。这种情况下,BubbleSort算法可以提前结束,而不必再进行后续的比较操作。
举个具体的例子来说明,对于输入序列 1 2 3 5 4:
- 在第一轮排序中,会先比较1和2,然后比较2和3,接着比较3和5,最后比较5和4,发现5和4的顺序不对,进行交换,exchange被设置为1。
- 在第二轮排序中,会继续比较1和2,2和3,3和4。因为在这一轮中没有发生任何交换,exchange保持为0。
- 根据exchange为0的判断,算法将会提前结束,因为在这一轮中没有发生交换,说明数组已经是有序的(除了最后的4和5位置互换),不需要再进行后续的比较和排序操作。
因此,exchange的作用在于提供了一种优化机制,可以在数组已经有序的情况下提前结束排序过程,减少不必要的比较操作,从而提高算法的效率。
那么当我们的数组有序的时候,也就是最好的情况,我们的复杂度是O(N),遍历一次发现exchange是0,停止循环

但是我们的时间复杂度算的是悲观保守的估计,所以即使优化了,我们的时间复杂度最终的结果还是O(N^2)!
当然这也给我们一个启示,一段代码中并不是只有一个复杂度,不同的情况有不同的复杂度
例三:二分查找的时间复杂度
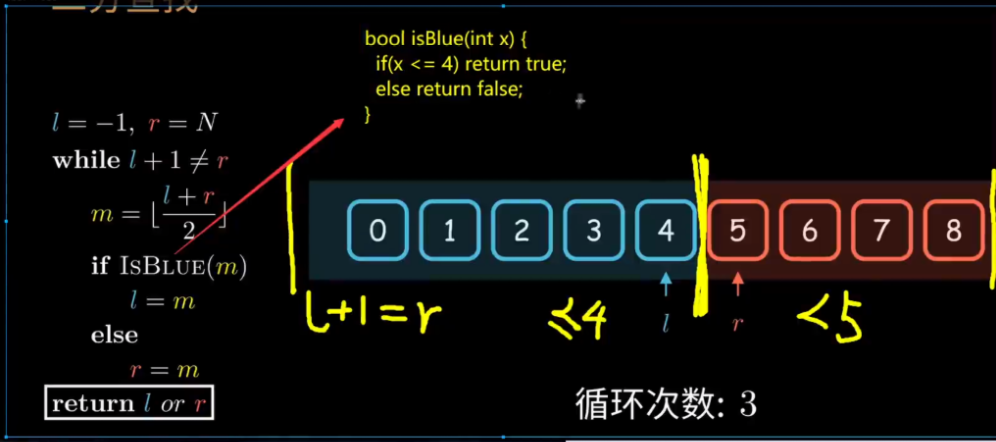
最好的情况:O(1)

最坏的情况:
分析最坏情况:
刚开始在N个数中找,接下来在N/2个数中找,接着在N/4数中找....
没找一次,次数+1,当我们有N个数据的时候,很容易得知我们只需要 Log₂x 就找出是否存在
用大O的渐进表示法得出时间复杂度:O(logN) (一般省略底数)
例四:阶乘递归的时间复杂度
long long Fac(size_t N) { if(0 == N) return 1; return Fac(N-1)*N; }
用大O的渐进表示法得出时间复杂度:O(N)
换句话讲就是:每次调用是O(1),但是调用N次
例五:斐波那契递归(二叉树)的时间复杂度
long long Fibonacci(size_t N) { return N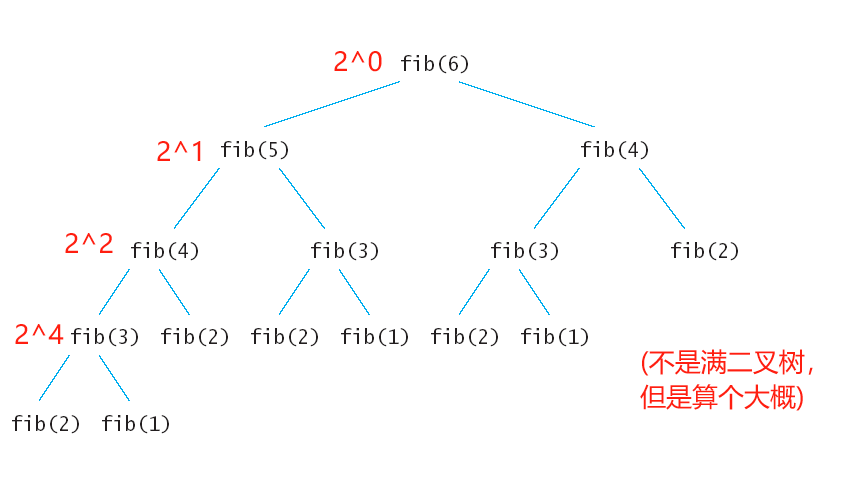
可以推导出最后一层的节点数量应该是2^n-1 (因为第1层是0次方)
那么我们的时间复杂度就转变为:2^0+2^1+...+2^n-1
我们可以用公式:

得知Sn=2^n-1
或者用错位相减法:

小羊表示:错位相减法yyds!!
最终可以得知 用大O的渐进表示法得出时间复杂度为:O(2^N)
说明斐波那契这个函数很挫,复杂度很高
1.6不同时间复杂度效率的比较
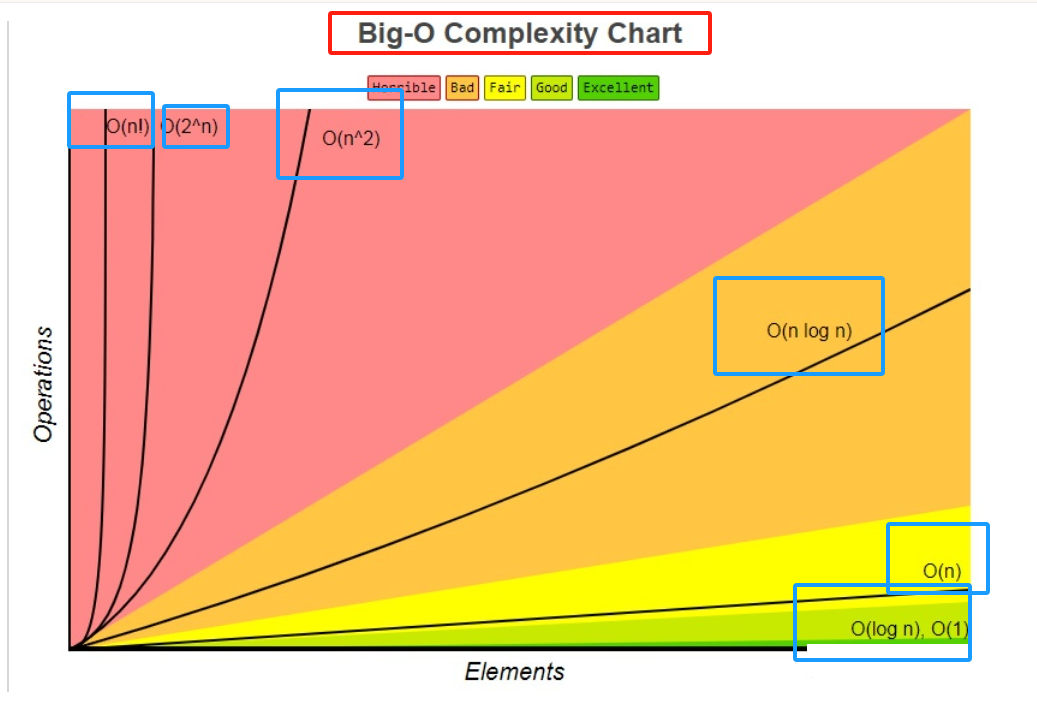
我们可以看到当测试数据很大时 O(logN) 和 O(1) 的效率几乎是一样的,所以二分查找是一种效率很高的算法,但是它也有一个缺陷,那就是它操作的数组元素必须是有序的。
二、空间复杂度(变量的个数)
2.1空间复杂度的概念
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟时间复杂度类似,也使用大O的渐进表示法。
而且我们找的变量,必须是这个程序临时占用的,额外占用的,别人给咱们的不算
谨记:时间是一去不复返的,需要累计;空间是可以重复利用的,不需要累计
2.2常见空间复杂度的计算
对于递归:
每次递归的开辟的大小 * 递归的次数
前言之空间可以重复利用
我们接下来要开始计算空间复杂度了,但是会有很多问题,所以我们先算一个程序
#include using namespace std; void f(int n) { int a=0; int *p=(int*)malloc(4*n); cout 1; if(check(q[mid],x)) { l=mid; } else { r=mid; } } //因为存在找不到的情况 if(q[r]==x)//r就是我们要的那个位置 { return r+1; } else { return -1; } } int main() { cin >> n >> m; for(int i=0;i> a[i]; } while(m--) { int x;//这里原先x写成数组是真没有必要 cin >> x; int res=binary_search(a,n,x); cout









