【数论】莫比乌斯反演巩固1

文章目录

• • • 前言
    • 洛谷P3455
    • 洛谷P1829
    • 洛谷P4449

      前言

      这里需要对莫反有一些基础。

      
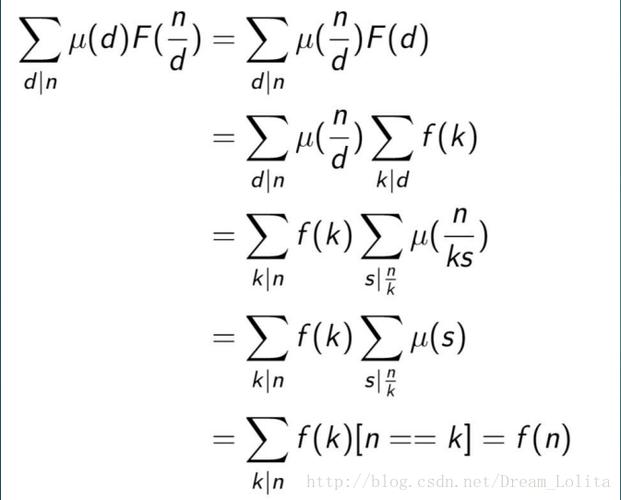      （图片来源网络，侵删）

      不会的可以点这里

      洛谷P3455

      题意：

      
      （图片来源网络，侵删）

      给定 a , b , d a,b,d a,b,d

      求 ∑ x = 1 a ∑ y = 1 b [ gCd ⁡ ( x , y ) = d ] \sum_{x=1}^a\sum_{y=1}^b[\gcd(x,y)=d] ∑x=1a​∑y=1b​[gcd(x,y)=d]

      1 ≤ n ≤ 5 × 1 0 4 1\leq n\leq5\times 10^4 1≤n≤5×104， 1 ≤ d ≤ a , b ≤ 5 × 1 0 4 1 \leq d \leq a,b \leq 5 \times 10^4 1≤d≤a,b≤5×104

      按照套路：

      ∑ x = 1 a ∑ y = 1 b [ gcd ⁡ ( x , y ) = d ] \sum_{x=1}^a\sum_{y=1}^b[\gcd(x,y)=d] ∑x=1a​∑y=1b​[gcd(x,y)=d]

      = ∑ x = 1 a d ∑ y = 1 b d [ gcd ⁡ ( x , y ) = 1 ] =\sum_{x=1}^{\frac{a}{d}}\sum_{y=1}^{\frac{b}{d}}[\gcd(x,y)=1] =∑x=1da​​∑y=1db​​[gcd(x,y)=1]

      = ∑ x = 1 a d ∑ y = 1 b d ∑ k ∣ gcd ⁡ ( x , y ) μ ( k ) =\sum_{x=1}^{\frac{a}{d}}\sum_{y=1}^{\frac{b}{d}}\sum_{k|\gcd(x,y)}\mu(k) =∑x=1da​​∑y=1db​​∑k∣gcd(x,y)​μ(k)

      = ∑ x = 1 a d ∑ y = 1 b d ∑ k = 1 μ ( k ) [ k ∣ gcd ⁡ ( x , y ) ] =\sum_{x=1}^{\frac{a}{d}}\sum_{y=1}^{\frac{b}{d}}\sum_{k=1}\mu(k)[k|\gcd(x,y)] =∑x=1da​​∑y=1db​​∑k=1​μ(k)[k∣gcd(x,y)]

      = ∑ k = 1 min ⁡ ( a d , b d ) μ ( k ) ∑ x = 1 a d ∑ y = 1 b d [ k ∣ gcd ⁡ ( x , y ) ] =\sum_{k=1}^{\min(\frac{a}{d},\frac{b}{d})}\mu(k)\sum_{x=1}^{\frac{a}{d}}\sum_{y=1}^{\frac{b}{d}}[k|\gcd(x,y)] =∑k=1min(da​,db​)​μ(k)∑x=1da​​∑y=1db​​[k∣gcd(x,y)]

      = ∑ k = 1 min ⁡ ( a d , b d ) μ ( k ) ⌊ a d k ⌋ ⌊ b d k ⌋ =\sum_{k=1}^{\min(\frac{a}{d},\frac{b}{d})}\mu(k)\left\lfloor\frac{\frac{a}{d}}{k}\right\rfloor\left\lfloor\frac{\frac{b}{d}}{k}\right\rfloor =∑k=1min(da​,db​)​μ(k)⌊kda​​⌋⌊kdb​​⌋

      数论分块解决即可。

      Code：

      #include
      #define int long long
      #define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
      using NAMEspace std;
      const int N=2e6+1,M=2e6+1;
      int t,n,m,k,ans=0;
      struct fy{
      	int prv[N],cnt,mu[N],sum[N];
      	bool pr[N];
      	void ola(int x){
      		pr[1]=mu[1]=1;
      		for(int i=2;i
      			if(!pr[i])
      				prv[++cnt]=i,mu[i]=-1;
      			for(int j=1;j
      				int u=i*prv[j];
      				pr[u]=1;
      				if(i%prv[j]==0){
      					mu[u]=0;
      					break;
      				}
      				else{
      					mu[u]=-mu[i];
      				}
      			}
      		}
      		for(int i=1;i
      	IOS;
      	A.ola(N-1);
      	cint;
      	while(t--){
      		cinn>;>m>>k;
      		n/=k,m/=k;
      		ans=0;
      		for(int l=1,r;l
      			r=min(n/(n/l),m/(m/l));
      			ans+=(A.sum[r]-A.sum[l-1])*(n/l)*(m/l);
      		}
      		cout
      	int prv[N],cnt,g[N],s[N];
      	bool pr[N];
      	void ola(int x){
      		pr[1]=g[1]=1;
      		for(int i=2;i
      			if(!pr[i])
      				prv[++cnt]=i,g[i]=(1-i+mod)%mod;
      			for(int j=1;j
      				int u=i*prv[j];
      				pr[u]=1;
      				if(i%prv[j]==0){
      					g[u]=g[i];
      					break;
      				}
      				else{
      					g[u]=g[i]*g[prv[j]]%mod;
      				}
      			}
      		}
      	}
      	void getsum(int x){
      		for(int i=1;i
      	IOS;
      	A.ola(N-1);
      	A.getsum(N-1);
      	cinnm;
      	int ans=0;
      	for(int i=1;i
      		ans+=A.s[n/i]*A.s[m/i]%mod*i%mod*A.g[i]%mod;
      		ans%=mod;
      	}
      	cout
      	int prv[N],cnt,g[N],s[N];
      	bool pr[N];
      	void ola(int x){
      		pr[1]=g[1]=1;
      		for(int i=2;i
      			if(!pr[i])
      				prv[++cnt]=i,g[i]=(1-i+mod)%mod;
      			for(int j=1;j
      				int u=i*prv[j];
      				pr[u]=1;
      				if(i%prv[j]==0){
      					g[u]=g[i];
      					break;
      				}
      				else{
      					g[u]=g[i]*g[prv[j]]%mod;
      				}
      			}
      		}
      	}
      	void getsum(int x){
      		for(int i=1;i
      	IOS;
      	A.ola(N-1);
      	A.getsum(N-1);
      	cinnm;
      	int ans=0;
      	for(int l=1,r;l
      		r=min(n/(n/l),m/(m/l));
      		ans+=A.s[n/l]*A.s[m/l]%mod*((A.g[r]-A.g[l-1]+mod)%mod)%mod;
      		ans%=mod;
      	}
      	cout
      	int prv[N],cnt,g[N],s[N];
      	bool pr[N];
      	inline int qmi(int x,int y){
      		int res=1;
      		while(y0){
      			if(y&1)
      				res=res*x%mod;
      			x=x*x%mod,y=1;
      		}
      		return res;
      	}
      	void ola(int x){
      		pr[1]=g[1]=1;
      		for(int i=2;i
      			if(!pr[i])
      				prv[++cnt]=i,g[i]=(qmi(i,k)-1+mod)%mod;
      			for(int j=1;j
      				int u=i*prv[j];
      				pr[u]=1;
      				if(i%prv[j]==0){
      					g[u]=g[i]*qmi(prv[j],k)%mod;
      					break;
      				}
      				else{
      					g[u]=g[i]*g[prv[j]]%mod;
      				}
      			}
      		}
      	}
      	void getsum(int x){
      		for(int i=1;i
      	IOS;
      	cintk;
      	A.ola(N-1);
      	A.getsum(N-1);
      	while(t--){
      		cinnm;
      		int ans=0;
      		for(int l=1,r;l
      			r=min(n/(n/l),m/(m/l));
      			ans+=(n/l)*(m/l)%mod*((A.g[r]-A.g[l-1]+mod)%mod)%mod;
      			ans%=mod;
      		}
      		cout