【计算机视觉】图像分割与特征提取——基于Log、Canny的边缘检测

个人简介： 

> 📦个人主页：赵四司机

> 🏆学习方向：JAVA后端开发 

> ⏰往期文章：SpringBoot项目整合微信支付

> 🔔博主推荐网站：牛客网 刷题|面试|找工作神器

> 📣种一棵树最好的时间是十年前，其次是现在！

> 💖喜欢的话麻烦点点关注喔，你们的支持是我的最大动力。

前言：

实验中要求能够自行评价Log、Canny算子在无噪声条件下和噪声条件下的分割性能。能够掌握分割条件(阈值等)的选择。完成规定图像的处理并要求正确评价处理结果，能够从理论上作出合理的解释。通过实验体会一些主要的分割算子对图像处理的效果，以及各种因素对分割效果的影响。

目录

一：相关概念

1.一阶导数二阶导数在图像边缘中的应用 

2.边缘检测基本步骤

3.好的边缘检测遵循的原则

4.二阶微分（差分）算子

二：拉普拉斯算子

1.等效式

2.拉普拉斯算子

​​​​3.拉普拉斯算子缺点 

三：高斯-拉普拉斯算子（Log）

1.相关概念

2.Log边缘检测

（1）基本特征

（2） 代码实战

（3）结果分析

四：Canny边缘检测

1.相概念

2.检测步骤

3.代码实战

4.结果分析 

五：思考总结

一：相关概念

1.一阶导数二阶导数在图像边缘中的应用 

• 一阶导数可以用于检测图像中的一个点是否是边缘点（判断一个点是否在斜坡上）；
• 二阶导数可以用于判断一个边缘像素是在边缘亮的一边还是暗的一边。 

  2.边缘检测基本步骤

  1. 滤波：边缘检测算法主要是基于图像强度的一阶和二阶导数，但导数的计算对噪声很敏感，因此必须使用滤波器来改善与噪声有关的边缘检测器的性能．需要指出，大多数滤波器在降低噪声的同时也导致了边缘强度的损失，因此，增强边缘和降低噪声之间需要折衷。
  2. 增强：增强边缘的基础是确定图像各点邻域强度的变化值．增强算法可以将邻域（或局部）强度值有显著变化的点突显出来．边缘增强一般是通过计算梯度幅值来完成的。
  3. 检测：在图像中有许多点的梯度幅值比较大，而这些点在特定的应用领域中并不都是边缘，所以应该用某种方法来确定哪些点是边缘点．最简单的边缘检测判据是梯度幅值阈值判据。
  4. 定位：如果某一应用场合要求确定边缘位置，则边缘的位置可在子像素分辨率上来估计，边缘的方位也可以被估计出来 

  3.好的边缘检测遵循的原则

  • 有好的检测率：

    •  最优的检测器应该能检测出所有真实边缘，而忽略噪声和其他瑕疵

  • 有好的局部化效果：

    •  检测到的边缘必须尽可能的靠近真实边缘

    • 对于每个真实边缘点，检测器必须返回一个点

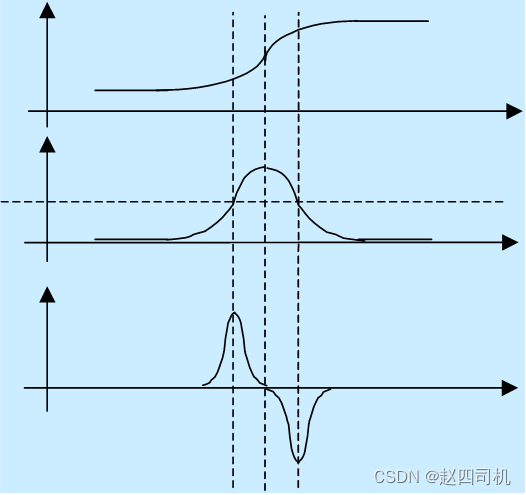
    4.二阶微分（差分）算子

            如果所求的一阶导数高于某一阈值，则确定该点为边缘点，这样做会导致检测的边缘点太多。 一种更好的方法就是求梯度局部最大值对应的点，并认定它们是边缘点，通过去除一阶导数中的非局部最大值，可以检测出更精确的边缘。 一阶导数的局部最大值对应着二阶导数的零交叉点。这样，通过找图像强度的二阶导数的零交叉点就能找到边缘点。

    

    二：拉普拉斯算子

    1.等效式

       

    2.拉普拉斯算子

        

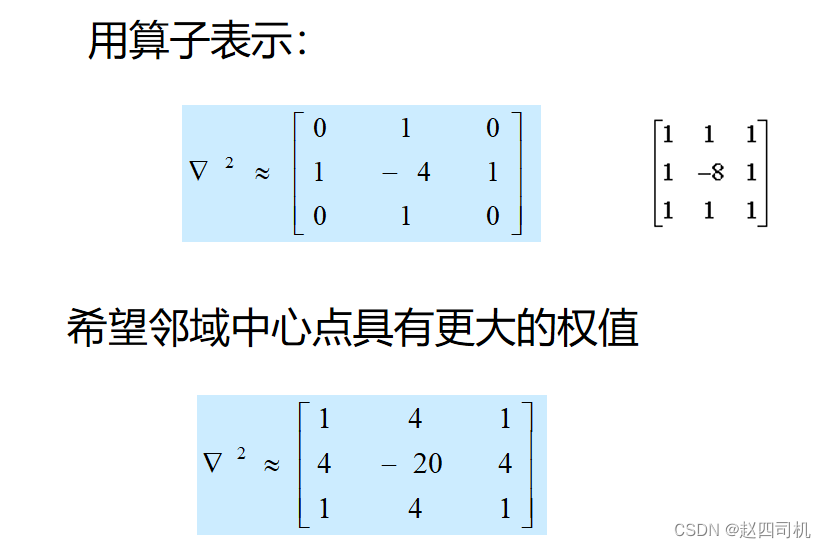
    • 二阶微分关心的是图像灰度的突变而不强调灰度缓慢变化的区域，对边缘的定位能力更强。
    •  Laplace算子是各项同性的，即具有旋转不变性

      ​​​​3.拉普拉斯算子缺点 

      • 拉普拉斯的二阶方向导数算子在机器视觉中并不常用， 因为任何包含有二阶导数的算子比只包含有一阶导数的算子更易受噪声的影响．甚至一阶导数很小的局部峰值也能导致二阶导数过零点．
      • 为了避免噪声的影响，必须采用特别有效的滤波方法．
      • 边缘的方向信息丢失。

        三：高斯-拉普拉斯算子（Log）

        1.相关概念

                Marr和Hildreth将高斯滤波和拉普拉斯边缘检测结合在一起，首先用高斯函数先进行低通滤波，然后利用拉普拉斯算子进行高通滤波并提取零交叉点，形成LoG（Laplacian of Gaussian）算法，也称之为拉普拉斯高斯算法． 

          

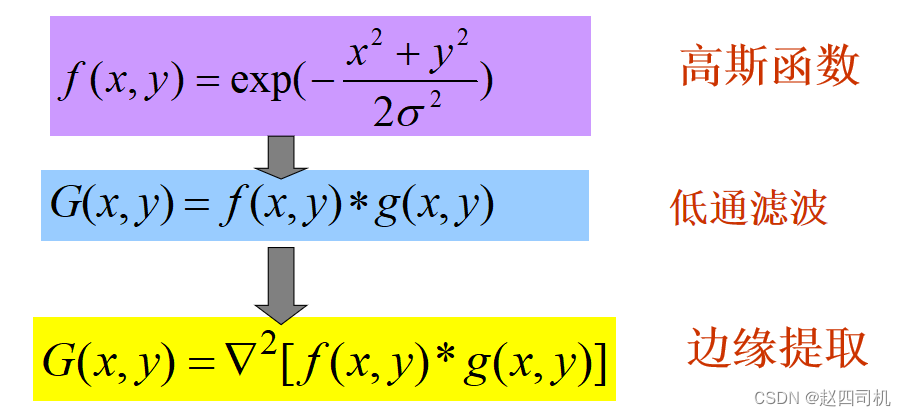
        2.Log边缘检测

        （1）基本特征

        • 平滑滤波器是高斯滤波器．
        • 采用拉普拉斯算子计算二阶导数．
        • 边缘检测判据是二阶导数零交叉点并对应一阶导数的较大峰值．
        • 使用线性内插方法在子像素分辨率水平上估计边缘的位置．  
        • 为什么使用高斯滤波器：
          • 逼近必须能够抑制噪声效应
          • 必须尽量精确地确定边缘的位置  
          • 但平滑去噪和边缘检测是一对矛盾，抑制噪声和边缘精确定位是无法同时得到满足的。应用高斯函数的一阶导数，在二者之间获得最佳的平衡。

          （2） 代码实战

          对图像加入不同噪声之后使用Log算子进行边缘检测：

          I = rgb2gray(imread('image\room.tif'));
          J=imnoise(f,'gaussian',0.1);
          BW1 = edge(I,'log',0.004); % σ=2
          BW2 = edge(J,'log',0.012,2); % σ=2
          figure(1),subplot(121),imshow(J),title('gaussian = 0.1');
          subplot(122),imshow(BW2);title('THRESH = 0.012 σ=2');
          imshow(BW1);title('σ=2')
          BW1 = edge(I,'log',0.004,3); % σ=3
          figure, imshow(BW1);title('σ=3')

            

          图3.4-1 Log算子（Sigma = 2）

            

          图3.4-2 Log算子（Sigma = 3）

            

          图3.4-3 Log算子（加入高斯0噪声，Sigma=2）

            

          图3.4-4 Log算子（加入强度0.1高斯噪声，THRESH=0.01，Sigma=2）

            

          图3.4-5 Log算子（加入强度0.1高斯噪声，THRESH=0.012，Sigma=2）

          （3）结果分析

                  Log算子我采用了matlab自带的函数进行实验，edge(I,'log',THRESH,SIGMA)

          可以看到有两个参数，THRESH表示函数忽略所有强度不大于THRESH值的边缘，SIGMA作为LoG过滤器的标准差。

                  LoG算子将高斯滤波和拉普拉斯边缘检测结合在一起，首先用高斯函数先进行低通滤波，然后利用拉普拉斯算子进行高通滤波并提取零交叉点。可以看到处理结果的图像边缘较平滑（见图3.4-1），是因为LoG算子不能检测边缘方向。而且在加入噪声之后，可以看到LoG算子对噪声十分敏感（见图3.4-3），不断调整参数，最终在参数THRESH=0.012，Sigma=2时得到较好的结果（见图3.4-5），但是还是损失了很多边缘信息。

          四：Canny边缘检测

          1.相概念

                  Canny边缘检测是一种非常流行的边缘检测算法，计算机视觉中用得最广的边缘检测器，是John Canny在1986年提出的(发表在PAMI)。

                  理论模型：加性噪声干扰的阶梯边缘（Step-Edge） Canny展示了高斯函数的一阶导紧密逼近最优化信噪比和局部化的边缘算子 

          2.检测步骤

          步骤1. 图像与高斯平滑滤波器卷积：

          

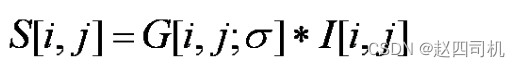
          步2. 使用一阶有限差分计算偏导数阵列P与Q：

          

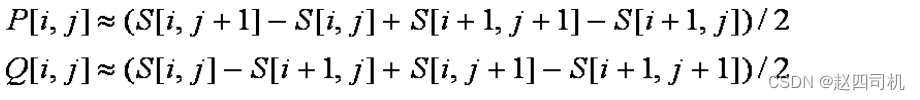
          步骤3.  计算梯度幅值与方向角:

          

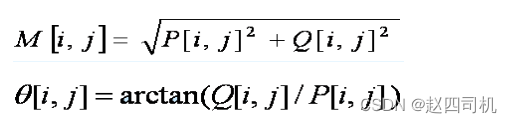
          步骤4. 非极大值抑制（NMS ） ：

              去掉幅值局部变化非极大的点．

              * 将梯度角离散为圆周的四个扇区之一，以便用3×3的窗口作抑制运算

          

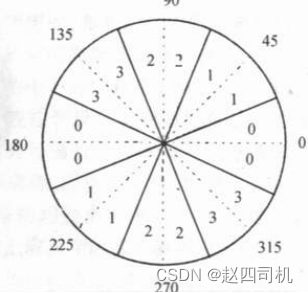
             * 方向角离散化：

              

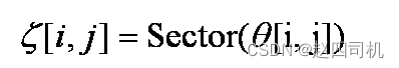
             * 抑制，得到新幅值图：

            

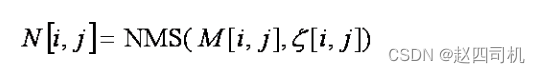
          步骤5. 阈值化

          取高低两个阈值作用于幅值图N[i,j]，得到两个边缘图：高阈值和低阈值边缘图。连接高阈值边缘图，出现断点时，在低阈值边缘图中的8邻点域搜寻边缘点。

          3.代码实战

          % I = rgb2gray(imread('image\room.tif'));
          % J=imnoise(I,'gaussian',0);
          % BW1 = edge(I,'canny',0.1);
          % BW2 = edge(J,'canny',0.175,1.9);
          % figure(2),subplot(121),imshow(J),title('加入gaussian噪声原图');
          % figure(2),subplot(122),imshow(BW2),title('加入gaussian噪声后检测结果');
          % figure(1),subplot(121),imshow(I),title('原图');
          % subplot(122),imshow(BW1);title('自带函数Canny边缘检测');
          % 自编程实现canny算子
          % image = rgb2gray(imread('image\lena.png'));
          % image=imnoise(image,'gaussian',0);
          image = imread('image\figure.png');
          image = rgb2gray(image);
          subplot(221);
          imshow(image);
          title('原始图像');
          image = double(image)/256;
          [m,n] = size(image);
          w = fspecial('gaussian');
          image_1 = imfilter(image,w,'replicate');
          subplot(222);
          imshow(int8(256*image_1));
          title('高斯滤波后的图像');
          % 梯度计算
          op = fspecial('sobel')/4;  % 用Sobel算子来求导数
          x = op';
          y =op;
          bx = imfilter(image_1,x,'replicate');
          by = imfilter(image_1,y,'replicate');
          b_abs = sqrt(bx.*bx+by.*by);        % 求梯度的幅值
          b_angle = angle(by-1i*bx);
          b_ang = b_angle/3.1416*180;         % 求梯度的方向
          % 梯度方向确定
          dir=ones(m,n);
          for r = 1:m
              for c = 1:n
                  if((b_ang(r,c)>=22.5 && b_ang(r,c)=-157.5 && b_ang(r,c)=67.5 && b_ang(r,c)=-112.5 && b_ang(r,c)=112.5 && b_ang(r,c)=-67.5 && b_ang(r,c)