0x0. 前言
这篇论文对应的链接为：https://openreview.net/pdf?id=tuzTN0eIO5 ，最近被ICLR 2024接收，但不少AI Infra的同行已经发现了这个工作的价值，并且已经开源在 https://github.com/sail-sg/zero-bubble-pipeline-parallelism ，在一些AI Infra相关的地方也存在一些讨论和介绍。比如 https://www.zhihu.com/question/637480969/answer/3354692418
所以来解读下这篇论文，此外作者的代码也可以很方便的在Megatron-LM中嵌入，总的来说是一个非常实用的Infra工作。后面论文解读完毕之后也会对ZB-H1代码实现进行解析。
0x1. 番外
这里简单对Megatron-LM提供的Pipline并行调度模式做一个理论讲解，这是读懂这篇文章的基础，由于整体的代码实现还是偏向复杂，所以这里偏向于理论讲解。
Pipline并行两篇比较关键的paper应该是GPipe和PipeDream，后面Meagtron在他们的基础上还做了工程优化比如vpp来减少bubble，我们只需要看懂 https://arxiv.org/pdf/2104.04473.pdf 里面的这两张图就可以了。
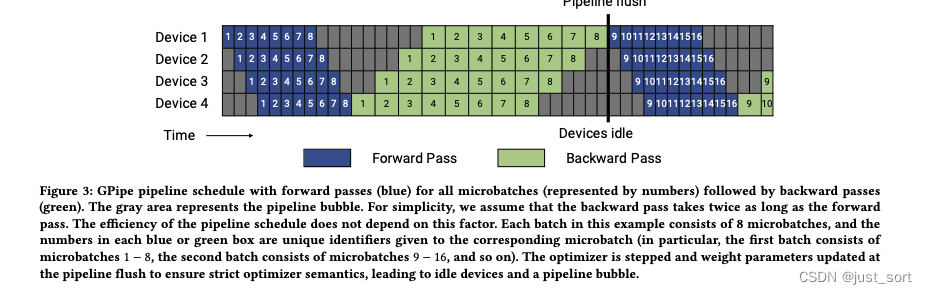
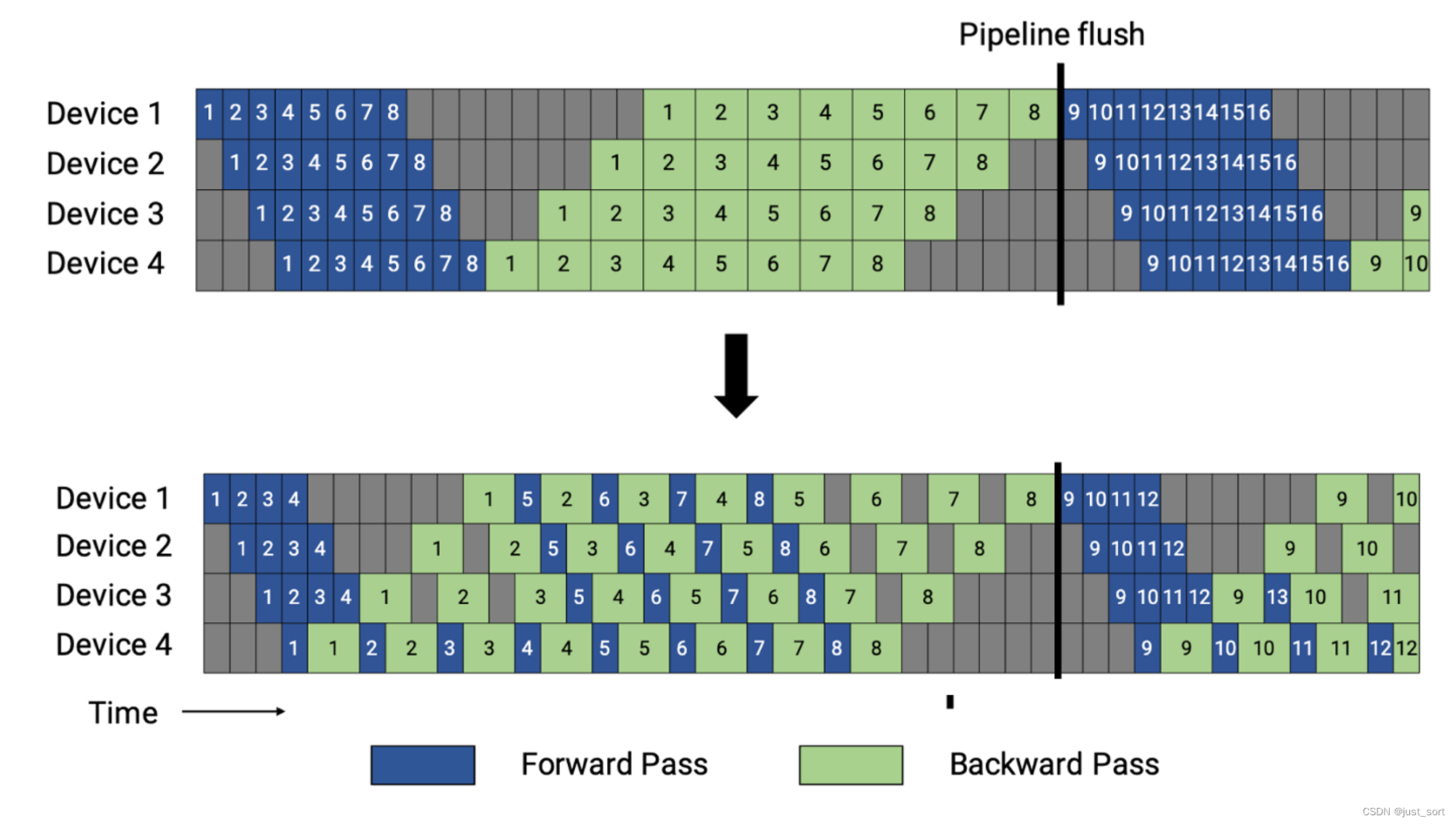
翻译下Figure3的描述：GPipe流水线schedule，所有micro-batch（以数字表示）均为前向传播（蓝色），然后为后向传播（绿色）。灰色区域表示流水线气泡。为简单起见，我们假设前向传播的时间是后向传播的两倍。流水线计划的schedule不取决于此时间因素。本例中的每个batch由8个micro-batch组成，每个蓝色或绿色框中的数字是给相应micro-batch的唯一标识符（比如，第一个batch由1− 8个micro-batch组成，第二个batch由micro-batch 9− 16组成等）。优化器在流水线刷新时进行步进（step）并更新权重参数，以确保严格的优化器语义。
这里说的严格的 Optimizer 语义是指，一个 batch 内的所有 micro-batch 的数据遇到的模型都是同一个版本的模型。为了达到这个效果，Megatron-LM 在一个 batch 的结尾引入了流水线 flush，即做一次跨设备的同步，然后再用 Optimizer 更新参数。
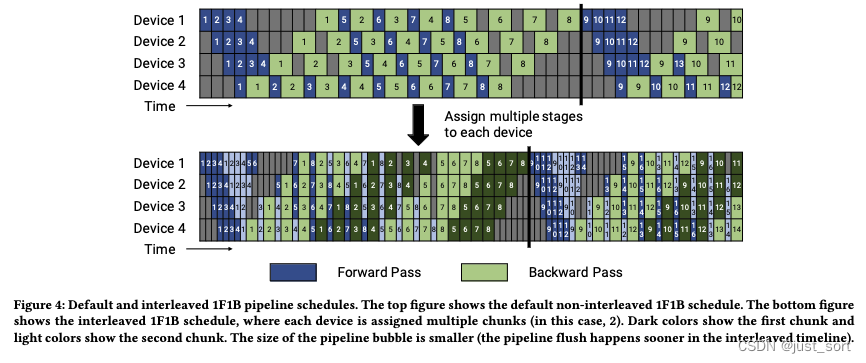翻译下Figure4的描述：默认和交错的1F1B Pipline Schedule。Figure4的上半部分显示了默认的非交错1F1B Schedule。Figure4的下半部分显示了交错的1F1B Schedule，其中每个设备被分配了多个chunks（在这个例子中是2个）。深色显示第一个chunk，浅色显示第二个chunk。Pipline并行的气泡的大小更小（在交错的1F1B Schedule时间线中，pipline flush更早发生）。这里交错的1F1B Schedule就是Meagtron-LM里面的VPP优化。
接着，我们首先来看上面的Figure3，为了看得更清楚把图放大：
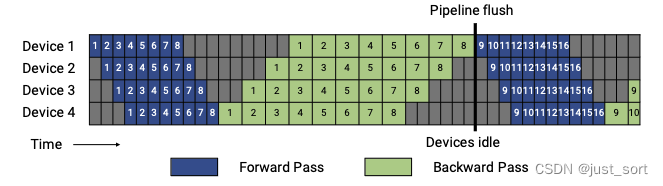
从这里可以看到GPipe的schedule是首先执行一个batch中所有micro-batch的前向传播，然后执行所有micro-batch的反向传播，这里假设micro-batch的大小为m（这里就是8），流水线的深度为d（这里就是4），一个 micro batch 的整个前向、整个后向的执行时间分别为 t f t_{f} tf 和 t b t_{b} tb. 则上图中在前向存在 p − 1 p-1 p−1 个 t f t_{f} tf 的气泡，在后向存在 p − 1 p-1 p−1 个 t b t_{b} tb 的 气泡，所以一个迭代的气泡 t p b t_{pb} tpb:
t p b = ( p − 1 ) ∗ ( t f + t b ) t_{pb}=(p-1)*(t_f+t_b) tpb=(p−1)∗(tf+tb)
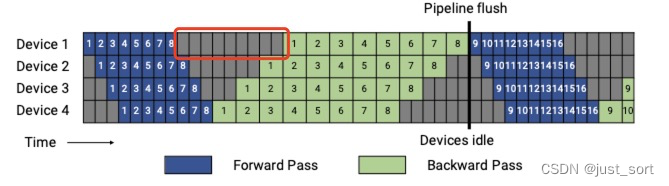
注意，这里的 t f t_f tf和 t b t_b tb的关系是假设 t b t_b tb是 t f t_f tf的两倍，也就是反向的计算时间是前向的两倍，所以 ( p − 1 ) ∗ ( t f + t b ) = 3 × 3 × t f = 9 × t f (p-1)*(t_f+t_b)=3\times 3\times t_f = 9 \times t_f (p−1)∗(tf+tb)=3×3×tf=9×tf，也就是说每个设备上有9个格子的气泡，我们可以数一下，确实如此。例如第一个stage上的红色框部分就是9个气泡。
而一个迭代理想的处理时间，即没有气泡的处理时间 t i d t_{id} tid:
t i d = m ⋅ ( t f + t b ) t_{id} = m\cdot(t_{f}+t_{b}) tid=m⋅(tf+tb)
这样气泡占比 Bubble time fraction:
t p b t i d = ( p − 1 ) m \frac{t_{pb}}{t_{id}} = \frac{(p-1)}{m} tidtpb=m(p−1)
这样为了降低气泡量，就需要 m ≫ p m \gg p m≫p. 但是每个 micro bath 前向的 Activation 都需要暂存直到依赖它的后向计算完成，这样 micro batch 数量过多，会导致显存占用增加过多。后面Pipline-Flush（https://arxiv.org/abs/2006.09503）论文里提供了一种改进策略：1F1B。核心部分就是下图：
解释一下这个图。对于GPipe来说流水线中最长驻留了 m m m 个未完成的 micro batch（上半部分图）. 而 1F1B 则限制其最多驻留流水线深度 p p p 个未完成的 micro batch，如此形成了上图中的下半部分的流水线。这个流水线的特点是一个迭代的时间没有变化，但是 p ≪ m p \ll m p≪m ，所以驻留的未完成的 micro batch极大减少，减少了显存峰值。（重点是减少了显存的峰值，但是气泡还是不变）
由于1F1B没有减少气泡大小，只是降低了显存占用峰值，所以后续Megatron-LM里在1F1B的基础上做了Interleaved 1F1B的优化，减少了流水线气泡，也就是VPP。
VPP的idea是于让 micro batch （micro batch size 更小）更多来减少气泡。方法是让一个 device 虚拟成 v v v 个 device，从计算 1个连续的 layer 段（有 x x x 个 layer）变成计算 v v v 个不连续的 layer 段（每段 layer 数量为 x / v x/v x/v）。比如之前 1F1B 时 device 1 负责 layer 1~4，device 2 负责 5~8，在 Interleaved 1F1B 下 device 1 负责 layer 1~2 和 9~10，device 2 负责 3~4 和 11~12，这样可以让流水线中每个 stage 更小，因而下个 stage 的等待时间更短，气泡更小。需要注意的是， m m m 需要是 p p p 的整数倍。如下图所示：
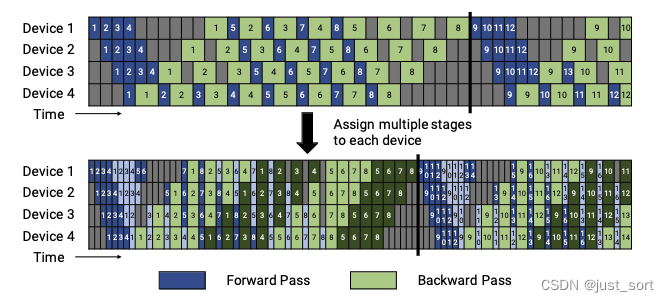
此时完成 v v v 个 layer 段中一个的前向、后向时间分别为 t f / v t_{f}/v tf/v 和 t b / v t_{b}/v tb/v, 流水线的气泡 t p b i n t . t_{pb}^{int.} tpbint.:
t p b i n t . = ( p − 1 ) ⋅ ( t f + t b ) v t_{pb}^{int.}=\frac{(p-1)\cdot(t_f + t_b)}{v} tpbint.=v(p−1)⋅(tf+tb)
然后可以计算出气泡占比：
t p b i n t . t i d = 1 v ⋅ ( p − 1 ) m \frac{t_{pb}^{int.}}{t_{id}} = \frac{1}{v}\cdot\frac{(p-1)}{m} tidtpbint.=v1⋅m(p−1)
可以看到，相比于1FB现在的气泡占比就减少到了 1 / v 1/v 1/v。但是流水线之间的通信量也增加了 v v v 倍。对于一个 pipeline stage，里面包括多个 Transformer layer，一个 microbatch 在流水并行的多个 pipeline stage 间的通信量是 2 b s h 2bsh 2bsh （考虑前向、后向各一次），采用 point-to-point 通信，且和 Transformer layer 数量无关 。所以现在相当于流水线的stage增加了，通信量也会增加。特别是当global的batch越来越大的时候，这个通信开销就会更显著。
所以，VPP似乎也不是一个鱼和熊掌兼得的方案，但我感觉这篇文章要解读的Paper在一定程度上是一个更完美的方案，相信完全有取代vpp的潜力。
这一节只是说Pipline的几个有影响力工作的核心idea，实际上在工程实现还有很多技巧例如通信加速之类的，之后有机会我们再分析。
0x2. 摘要
大概就是说这个paper提出了一个新的流水线调度算法，实现了流水线并行同步训练时的的零气泡。我理解这里的同步训练指的就是1F1B中一个 batch 内的所有 micro-batch 的数据遇到的模型都是同一个版本的模型。然后这个改进基于一个关键的观察就是反向计算可以分成两部分，一部分计算输入的梯度，另一部分计算参数的梯度。此外paper还提到，他们开发了一个算法可以根据特定模型配置和内存限制自动找到最佳调度。另外，为了实现真正的零气泡，作者引入了一种新技术来绕过优化器步骤中的同步。实验评估结果显示，这种调度算法在类似的内存限制下，吞吐量比1F1B调度高出至多15%。当内存限制放宽时，这个数字可以进一步提高到30%。
0x3. 介绍
第，1，2，3段可以不看，就是番外介绍到的知识。从第4段开始看下：
重点就是说目前1F1B仍然存在流水线气泡的问题，然后作者发现过以更细的粒度表示和调度计算图，可以进一步优化Pipline并行中的气泡。
一般神经网络为组织为一些堆叠的层。每一层有前向传播和反向传播。前向传播中，输入 x x x通过 f ( x , W ) f(x, W) f(x,W)映射到输出 y y y。反向传播对于训练至关重要，涉及两个计算： ∇ x f ( x , W ) ⊤ d ℓ d y \nabla_x f(x, W)^\top \frac{d\ell}{dy} ∇xf(x,W)⊤dydℓ 和 ∇ W f ( x , W ) ⊤ d ℓ d y \nabla_W f(x, W)^\top \frac{d\ell}{dy} ∇Wf(x,W)⊤dydℓ ，它们计算相对于输入 x x x和层的参数 W W W的梯度。为方便起见，我们使用单个字母 B B B和 W W W分别表示这两个计算，以及使用 F F F表示前向传播，如Figure1所示。
传统上， B B B和 W W W被分组并作为单一的后向函数提供。这种设计在概念上对用户友好，并且对于数据并行（DP）来说恰好工作良好，因为在第 i i i层的权重梯度的通信可以与第 i − 1 i-1 i−1层的后向计算重叠。然而，在流水线并行（PP）中，这种设计不必要地增加了顺序依赖的计算，即第 i − 1 i-1 i−1层的 B B B依赖于第 i i i层的 W W W，这通常对流水线并行的效率不利。基于分割的 B B B和 W W W，paper提出了新的Pipline调度算法，大大提高了Pipline并行的效率。
paper其它部分的行文方式如下：在第2节中，介绍了基于 F F F、 B B B和 W W W的执行时间相同的理想假设下的手工调度。随后，在第3节中，我们取消了这个假设，并提出了一个在更现实条件下工作的自动调度算法。为了实现零气泡，第4节详细介绍了一种方法，该方法在优化器步骤中绕过了同步的需要，但保留了同步训练语义。通过在不同设置下将paper的方法与基线方法进行实证评估来结束本文。
需要注意，作者的目标不是探索大规模分布式训练的一般混合策略。相反，作者特别致力于提高Pipline并行调度的效率，并通过与基线的比较来证实。作者的方法与数据并行（ D P DP DP）、张量并行（ T P TP TP）和 Z e R O ZeRO ZeRO策略是正交的，它可以作为大规模训练中 P P PP PP部分的并行替代品。
0x4. 手工编排的Pipline Schedule
基于将B和W分开可以减少顺序依赖并因此提高效率的关键观察，我们从常用的1F1B调度开始重新设计Pipline并行。如Figure 2所示，1F1B以一个预热阶段开始。在这个阶段，每个workers（GPU）执行不同数量的前向传播，每个stage通常比它后面的stage多执行一次前向传播。预热阶段之后，每个workers过渡到一个稳定状态，在这个状态中，他们交替执行一次前向传播和一次后向传播，确保在各个阶段之间均匀分配工作负载。在最后阶段，每个worker处理未完成的micro batch的后向传播，完成这个batch。
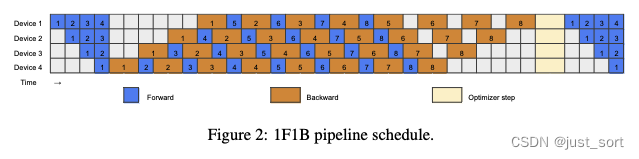
在paper改进的版本中，将反向传播分为B和W两个阶段，仍然必须确保同一个micro batch中的F和B在Pipline stages之间保持顺序依赖。然而，相同阶段的W可以在对应的B之后的任何地方灵活地安排。这允许策略性地放置W来填充Pipline的气泡。 之前也有一些方法改进了1F1B的调度，以不同的方式在气泡大小和显存占用之间进行权衡。在本节中，paper介绍了两个有趣的手工Pipline调度，以展示更细粒度在减少Pipline气泡方面的巨大潜力（见Figure 3）。为了在让初步设计更易懂，我们假设F、B和W的时间成本是相同的，这一假设也被早期的研究（Narayanan et al., 2021; Huang et al., 2019）所共享。然而，在第paper的第3节中，我们重新评估了这一假设，以在现实场景中优化Pipline调度的效率。
0x4.1 内存高效的Schedule
Paper提出的第一个手工调度，名为ZB-H1，确保所有worker的最大峰值内存使用量不超过1F1B的使用量。ZB-H1通常遵循1F1B的调度，但它根据预热micro batch的数量调整W的开始点。这确保所有worker维持相同数量的in-fight micro-batch。因此，如Figure 3（顶部）所示，气泡大小减少到1F1B大小的三分之一。这种减少是因为与1F1B相比，所有worker更早地启动B，并且尾端的气泡被较晚启动的W阶段填补。由于W通常比B使用更少的内存（见下面的Table 1），另外第一个worker有最大的峰值内存使用量，这与1F1B一致。
0x4.2 零气泡Schedule
paper指出当允许比1F1B更大的内存占用，并且有足够数量的micro batch时，可以实现一个零气泡调度，我们将其标记为ZB-H2。如上面Figure 3（底部）所示，我们在预热阶段引入更多的F来填补第一个B之前的气泡。我们还在尾部重新排序W，这将Pipline的布局从梯形变为平行四边形，消除了Pipline中的所有气泡。还要强调的是，在这里，优化器步骤之间的同步被移除了，paper的第4节讨论如何安全地完成这一点。
0x4.3 量化分析
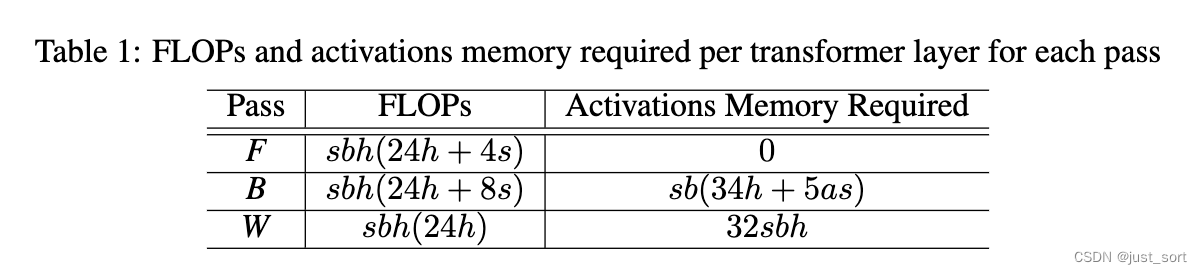
先做了一些约定，使用 p p p来表示流水线stage的数量，用 b b b来表示每个micro batch的大小。对于Tranformer架构，用 a a a表示注意力头的数量，用 s s s表示序列长度，用 h h h表示隐藏维度的大小。使用记号 M B M_B MB/ M W M_W MW来表示存储一个 B B B/ W W W激活所需的内存，以及 T F / T B / T W T_F/T_B/T_W TF/TB/TW来表示一个 F / B / W F/B/W F/B/W的运行时间。为了简单起见，我们仅对Transformer架构进行定量分析，使用类似于GPT-3的经典设置，其中前馈内部的隐藏维度大小为 4 h 4h 4h，每个注意力头的维度大小为 h / a h/a h/a。
正如Narayanan等人（2021年）所述，paper在计算FLOPs时只考虑矩阵乘法操作，因为它们在Transformer层中贡献了大部分的计算。在前向传播中的每一个矩阵乘法操作，对应的反向传播中有两个具有相同FLOPs的矩阵乘法操作（见上面的Figure 1的B和W）。计算Transformer层FLOPs的近似公式在表1中。我们可以看到 T W
这里的意思是如果当前处于BWF的模式或者在rank0或者当前的迭代处于最后一个micro batch，就不分割B和W，这里的BWF模式应该就是表示ZB-H1的1F1B1W稳定状态，这是通过当前micro batch的index和rank的大小关系来判断的，不是很确定这样是不是完全正确，但从ZB-H1的图来看这样判断是没问题的。
比如我们看流水线的第4个stage，只有当micro batch的index为4时才出现了B和W分离调度。WeightGradStore.flush()表示当前stage的每一个micro batch执行完之后我们要把所有的W Cache起来，然后if i >= rank > 0: # delay W by rank这个操作发生在最后一个micro batch，这个时候我们就需要更新W了。这里可能那个有个必须了解Meagtron Pipline并行才可以理解的问题，在上面的图里，这里的最后一个micro batch表示的是8吗？不是，是4，为什么？因为在Megatron-LM的pipline里面分成了warmp和1f1b和cooldow阶段，然后这里的最后一个micro batch指的是在1F1B的最后一个micro batch，而总的micro batch是8，warmup的micro batch是4，那么1F1B阶段的micro batch就是4了。
最后在cooldown阶段，代码的修改是这样：
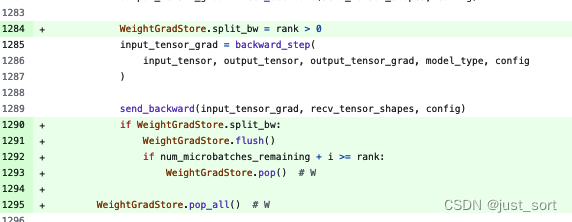
这里的1295行对应的就是下面红色的部分：
而1292行这个判断对应cooldown阶段的1F1B1W。应该对应这部分：
感兴趣的读者可以关注他们的开源仓库：https://github.com/sail-sg/zero-bubble-pipeline-parallelism
0x11. Pipline并行 PlayGround
作者团队提供了一个令人眼前一亮的流水线Schedule PlayGround，访问地址如下：https://huggingface.co/spaces/sail/zero-bubble-pipeline-parallellism
给定流水线并行的一些关键参数之后就可以对流水线Schedule自动作图：
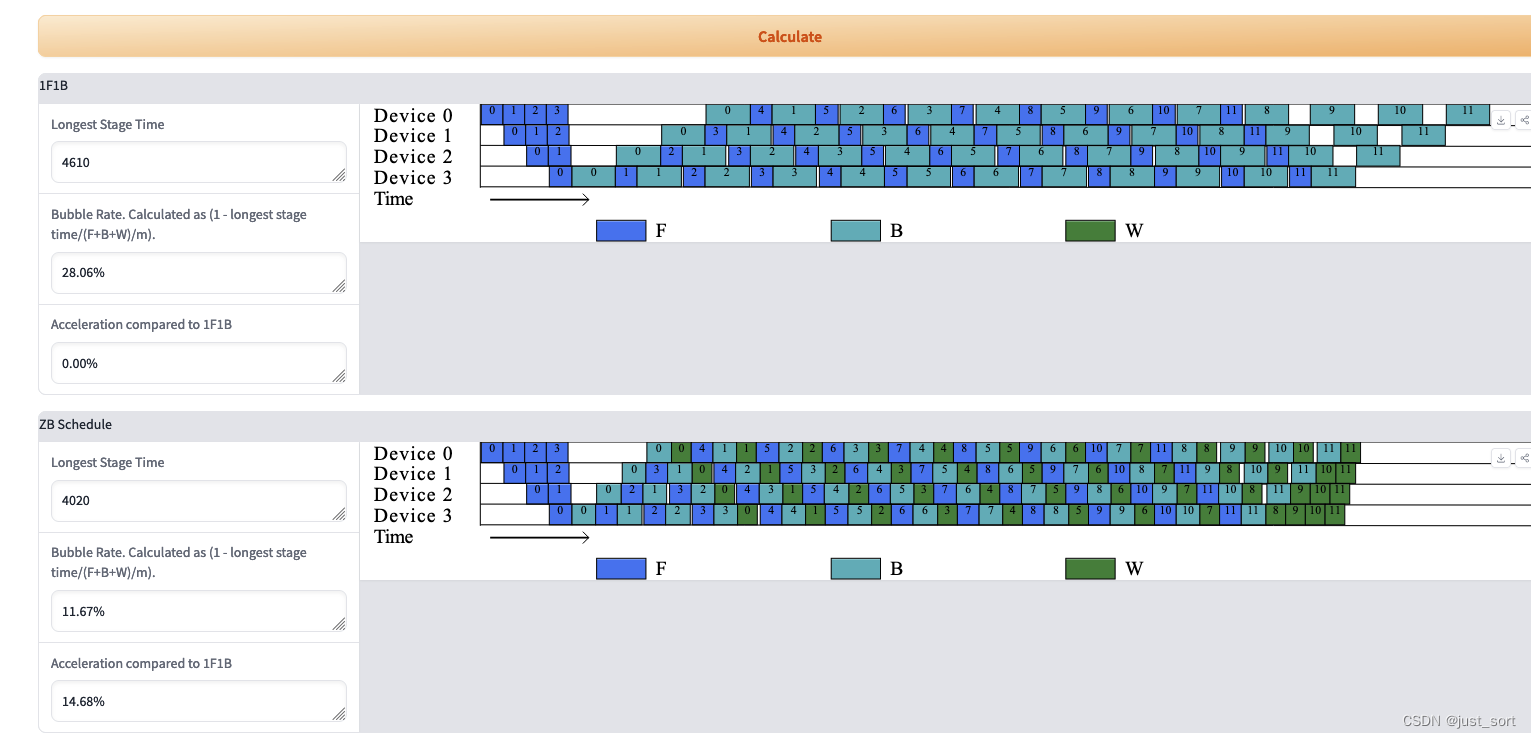
个人感觉paper的学术和工程价值都不错，有完全取代VPP的势头，推荐同行阅读。
0x12. 参考
- https://strint.notion.site/Megatron-LM-86381cfe51184b9c888be10ee82f3812
