人工智能顶会ICLR2023《Is Conditional Generative Modeling all you need for Decision Making?》论文解读

Is Conditional Generative Modeling all you need for Decision Making?

• 1.引言
• • 条件生成建模
  • 传统强化学习面临的挑战
  • 作者的研究动机与创新点
  • 2.重要概念
  • • 强化学习
    • 扩散概率模型
    • 传统的强化学习到生成建模的转变
    • 本文提出方法的总体框架
    • 3.决策扩散的概念和设计
    • • 扩散状态（Diffusing Over States）
      • 逆向动力学（Acting with Inverse-Dynamics）
      • 无分类器指导规划（Planning with Classifier-Free Guidance）
      • 超越回报的条件化（Conditioning Beyond Returns）
      • 训练与实现细节

        1.引言

        条件生成建模

        条件生成建模是一种机器学习技术，用于生成数据样本，这些样本基于给定的条件或上下文。它与传统的生成模型不同，后者生成数据而不依赖于任何条件或输入。条件生成建模常见于深度学习，特别是在生成对抗网络（GANs）和变分自编码器（VAEs）中。这种方法在图像合成、文本生成、语音合成等领域表现出色。它使模型能够在给定特定条件（如标签、描述或其他数据点）的情况下，生成更加精准和特定的输出。

        传统强化学习面临的挑战

        1. 样本效率低：强化学习通常需要大量的数据才能学习有效的策略，这在现实世界应用中是一个重大障碍。
        2. 稀疏奖励问题：在很多情况下，有效的反馈（奖励）很少，使得学习过程变得困难。
        3. 探索与利用的平衡：决定何时探索新策略和何时利用已知策略是强化学习中的关键问题。
        4. 环境模型的复杂性：对于复杂或不确定的环境，建立一个准确的模型非常挑战，这限制了算法的有效性。
        5. 泛化能力：强化学习模型在从训练环境到新环境转移时，泛化能力往往有限。

        作者的研究动机与创新点

        探索条件生成建模在顺序决策制定中的应用，特别是在离线强化学习的环境下。作者认为，通过使用条件生成模型（如扩散模型），可以绕过传统离线强化学习中的复杂动态规划过程，并解决价值函数估计的不稳定性等问题。

        论文的创新点在于提出了一种名为**“决策扩散器”（Decision Diffuser）的框架**，它使用条件扩散模型来进行决策生成。这种方法不仅可以最大化回报，还可以灵活地结合多种约束和技能，以产生新的行为。这种方法在实验中显示出优于传统方法的性能，展示了条件生成模型在决策制定中的潜力。

        

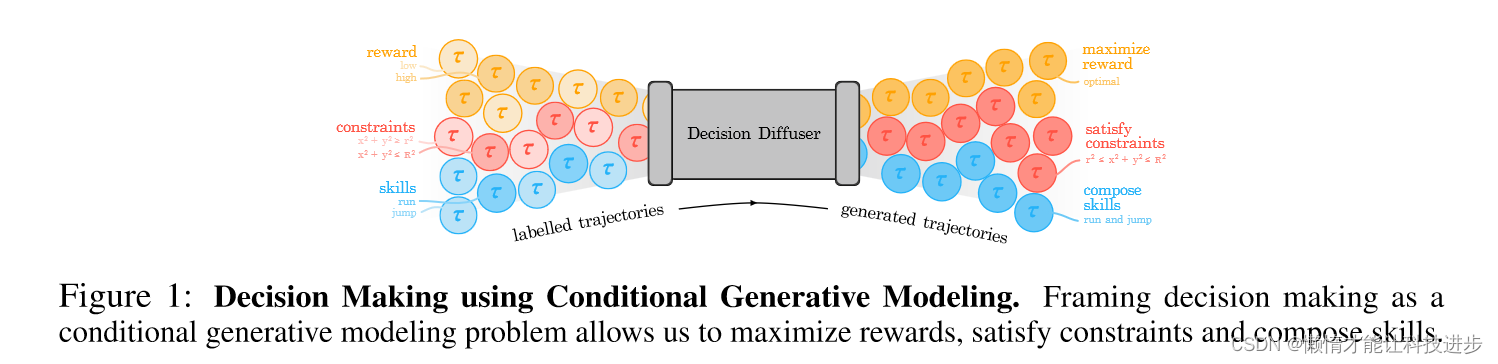
        图中展示了利用条件生成模型进行决策制定的框架。在这个框架中，决策扩散器（Decision Diffuser）作为核心组件，接受不同类型的输入并生成轨迹。具体来说，图中的内容可以解释如下：

        1. 有标签的轨迹（Labelled Trajectories）：

           • 有标签的轨迹是训练数据，包含了不同的条件，如回报（reward）、约束（constraints）和技能（skills）。
           • 这些轨迹按照它们所实现的目标或属性进行了分类。例如，回报可以是低（low）或高（high）；约束可以是数学表达式如 x 2 + y 2 ≤ r 2 x^2 + y^2 \leq r^2 x2+y2≤r2；技能可以是运行（run）或跳跃（jump）。

           • 决策扩散器（Decision Diffuser）：

             • 决策扩散器是一个条件生成模型，它使用有标签的轨迹来学习如何生成满足特定条件的新轨迹。
             • 它可以同时考虑多个条件，如最大化回报，满足特定的约束，以及组合不同的技能。

             • 生成的轨迹（Generated Trajectories）：

               • 生成的轨迹是模型输出的结果，它们应该反映输入条件的组合。
               • 这些轨迹旨在实现特定的目标，如最大化回报（maximize reward）、满足特定的约束（satisfy constraints），以及组合技能（compose skills）。

        总体来说，这幅图表展示了如何将决策制定问题框架化为一个条件生成建模问题，通过这种方式可以最大化回报，满足约束，并组合不同的技能。这种方法允许使用机器学习的方法来自动化和优化复杂决策过程。

        2.重要概念

        强化学习

        是一种机器学习方法，它使智能体能够在环境中做出决策以最大化累积奖励。它包括以下关键概念：

        1. 智能体（Agent）：进行决策的实体。
        2. 环境（Environment）：智能体交互的系统。
        3. 状态（State）：环境的当前情况。
        4. 行为（Action）：智能体可以执行的操作。
        5. 奖励（Reward）：智能体行为的即时反馈。
        6. 策略（Policy）：智能体选择行为的规则。

        智能体通过探索环境并学习从状态到行为的最佳映射来优化其策略，从而在长期内最大化累积奖励。强化学习在游戏、机器人导航、资源管理等领域有广泛应用。

        扩散概率模型

        扩散概率模型是一种用于生成数据的机器学习模型，它模拟了一种从无序状态（如高斯噪声）逐步生成有序数据（如图像或文本）的过程。这个过程类似于物理中的扩散过程，从而得名。扩散模型通过逐步减少噪声并逐步引入数据特征的方式工作，最终生成高质量的数据样本。这种方法已经被证明在生成高复杂度和高质量的数据方面非常有效，例如在图像和音频合成中。

        扩散概率模型中的关键公式包括：

        1. 噪声添加公式：它描述了如何逐步将噪声添加到数据中。这通常是通过线性插值的形式实现的，如 x t = α t x t − 1 + 1 − α t ϵ x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon xt​=αt​ ​xt−1​+1−αt​ ​ϵ，其中 ϵ \epsilon ϵ是高斯噪声， α t \alpha_t αt​是时间步t的噪声比例。

        2. 逆过程公式：在逆过程中，模型试图预测并去除噪声。这个过程的一个关键部分是估算给定噪声数据下的原始数据分布，通常表示为 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p(xt−1​∣xt​)。

        这些公式是建立扩散模型的基础，涉及概率论和统计学的概念，特别是在处理高斯分布时。模型的训练和优化通常依赖于这些数学表达式。

        传统的强化学习到生成建模的转变

        体现在几个关键方面：

        1. 目标变化：在传统RL中，目标是学习一个策略或价值函数来指导行为。而在生成建模中，目标是直接从环境数据中学习决策的概率分布。
        2. 数据处理：生成建模强调从大量数据中学习模式，而不是专注于单个状态或行动的最优选择。
        3. 泛化能力：生成模型通常能更好地泛化到新的、未见过的环境状态，这在传统RL中是个挑战。
        4. 复杂环境处理：生成模型能更有效地处理高维度和复杂的环境，这在传统方法中往往更为困难。

        本文提出方法的总体框架

        

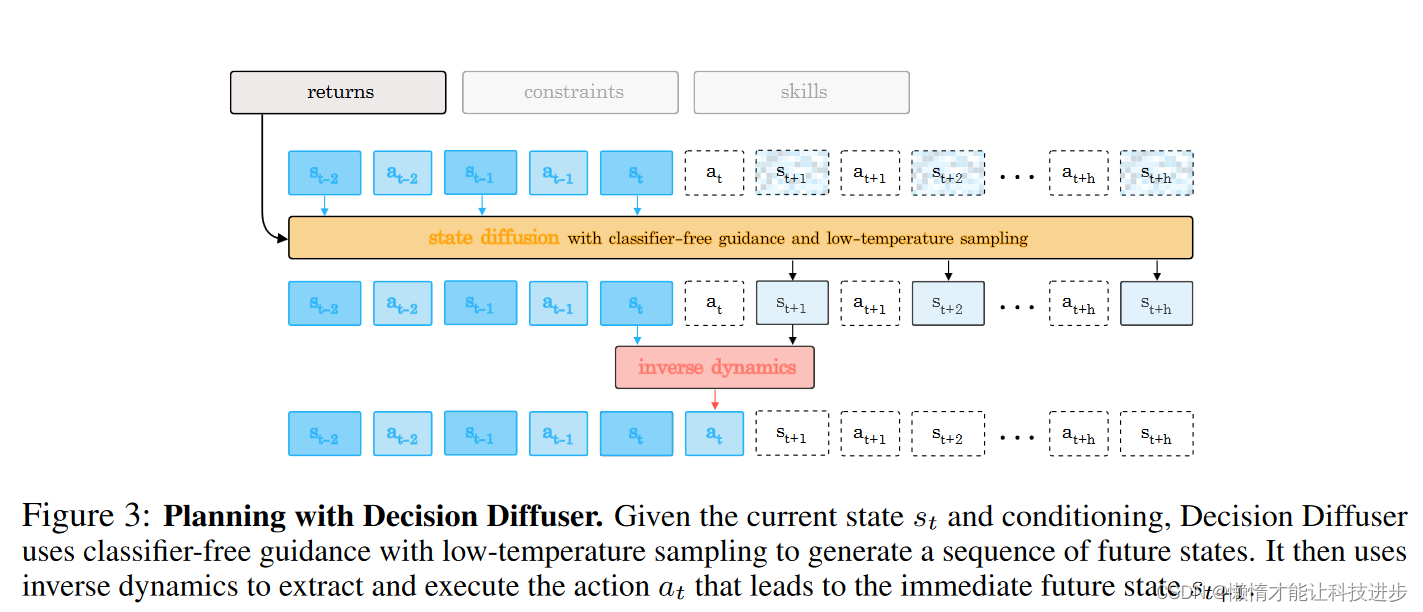
        图中描绘了使用决策扩散器（Decision Diffuser）进行规划的过程。以下是该过程的详细解释：

        1. 输入条件：图中最上方的框表示输入条件，包括回报（returns）、约束（constraints）和技能（skills），这些条件用于指导决策扩散器生成特定特性的未来状态序列。

        2. 状态扩散（State Diffusion）：黄色框代表状态扩散过程，它使用无分类器指导（classifier-free guidance）和低温度采样（low-temperature sampling）来生成一系列未来的状态。无分类器指导是一种避免使用显式分类器的生成方法，而低温度采样则使得生成的状态更加集中于高概率区域，从而提高生成质量。

        3. 逆向动力学（Inverse Dynamics）：红色框代表逆向动力学模型，它用于从状态序列中提取和执行动作。具体来说，它根据当前状态 s t s_t st​和下一个状态 s t + 1 s_{t+1} st+1​来确定应该执行的动作 a t a_t at​。

        4. 状态和动作序列：蓝色框表示已知的状态和动作序列。每个状态 s s s都对应一个动作 a a a，并且状态之间通过动作相互连接。决策扩散器计划的目标是产生一个未来的状态序列，从 s t s_t st​ 到 s t + h s_{t+h} st+h​，其中 h h h 是规划的时间范围。

        5. 生成的动作和状态：图中的箭头表示从当前状态 s t s_t st​ 通过状态扩散和逆向动力学生成的动作 a t a_t at​和未来的状态 s t + 1 s_{t+1} st+1​。这个过程可以一直继续，直到达到规划的时间范围终点。

        总体而言，这幅图展示了如何结合状态扩散和逆向动力学来进行决策规划，它体现了决策扩散器在给定当前状态和条件下，如何生成一系列可能的未来状态，并确定通往这些状态的动作序列。

        3.决策扩散的概念和设计

        决策扩散的概念和设计基于条件生成建模，旨在解决顺序决策制定问题。这种方法的核心在于，它不通过传统的强化学习（RL）视角来看待决策制定，而是通过条件生成模型的视角来处理。这种转变使得研究者可以避免依赖于时间差分（TD）学习和避免分布偏移的风险。

        具体来说，决策扩散器（Decision Diffuser）采用了一种称为返回条件扩散模型的策略。通过这种方法，可以绕过动态规划的需要，从而消除传统离线RL带来的许多复杂性。决策扩散器在训练过程中可以考虑单个约束或技能，从而在测试时产生满足多个约束或展示技能组合的行为。这些结果表明，条件生成建模是决策制定的一个强大工具。

        决策扩散器的目标是估计条件数据分布 p θ p_\theta pθ​，以便稍后从关于轨迹 τ \tau τ信息 y ( τ ) y(\tau) y(τ) 中生成轨迹的一部分 x 0 ( τ ) x_0(\tau) x0​(τ)。这里的 y y y可以包括轨迹下的回报、轨迹满足的约束或轨迹展示的技能。生成模型按照条件扩散过程构建，其中 q q q表示前向添加噪声过程，而 p θ p_\theta pθ​则是反向去噪过程

        总体而言，决策扩散器提供了一种新的角度和方法来处理顺序决策制定问题，特别是在复杂和约束丰富的环境中。

        

        图中描述了一个2D机器人导航环境的例子，并展示了如何使用条件生成模型生成满足特定约束的轨迹。具体内容如下：

        1. 环境（Environment）：

           • 左侧第一个图显示了一个二维的机器人导航环境，其中有一个起始点（标记为黑色点），机器人需要在环境中移动。

           • 训练数据集（Training Dataset）：

             • 第二和第三个图展示了从环境中衍生出的轨迹数据集，这些轨迹满足特定的数学约束。红色点表示在较小圆内的轨迹终点（满足 x 2 + y 2 ≤ r 2 x^2 + y^2 \leq r^2 x2+y2≤r2），黄色点表示在较大圆内的轨迹终点（满足 x 2 + y 2 ≤ R 2 x^2 + y^2 \leq R^2 x2+y2≤R2），这些圆圈代表不同的约束条件。

             • 轨迹生成（Generation）：

               • 右侧第四个图展示了使用条件生成模型生成的轨迹。蓝色点表示模型生成的轨迹，这些轨迹满足组合约束（即最终位置位于两个同心圆之间，满足 r 2 ≤ x 2 + y 2 ≤ R 2 r^2 \leq x^2 + y^2 \leq R^2 r2≤x2+y2≤R2）。

        这幅图表说明了条件生成模型如何能够学习并理解复杂约束的概念，并在新轨迹的生成中应用这些约束，从而展示了这种模型在执行特定任务时的灵活性和能力。

        扩散状态（Diffusing Over States）

        1. 过程概述：与图像处理中的扩散过程类似，该过程被应用于状态和行动的建模。然而，在强化学习环境中，直接对行动使用扩散过程存在实际问题。

        2. 状态与行动的差异：在强化学习中，状态通常是连续的，而行动更为多样化，往往是离散的。此外，行动序列（例如联合扭矩）往往具有较高的频率和较低的平滑度，这使得它们更难以预测和建模。

        3. 选择只对状态进行扩散：鉴于这些实际问题，决策扩散器选择仅对状态进行扩散，而不涉及行动。状态的扩散过程表示为 x k ( τ ) = ( s t , s t + 1 , . . . , s t + H − 1 ) k x_k(\tau) = (s_t, s_{t+1}, ..., s_{t+H-1})_k xk​(τ)=(st​,st+1​,...,st+H−1​)k​，其中 τ \tau τ表示轨迹， s t s_t st​表示在时间步 t t t的状态， H H H是轨迹的长度， k k k表示扩散过程中的时间步。

        通过这种方法，决策扩散器可以有效地处理状态空间的复杂性，并避免直接处理行动的困难。这种仅对状态进行扩散的方法，使得模型能够更加有效地生成和预测未来的状态序列。

        ![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/7478891a437f458f8e3be6ccf855697b.png

        逆向动力学（Acting with Inverse-Dynamics）

        逆向动力学（Acting with Inverse-Dynamics）是指根据两个连续状态推断出导致这种状态变化的行动的过程。在决策扩散器（Decision Diffuser）中，这是一个关键步骤，用于从状态序列中定义和执行控制器（controller）所需的行动。

        在具体实现上，给定连续的两个状态 s t s_t st​ 和 s t + 1 s_{t+1} st+1​，逆向动力学模型 f ϕ f_\phi fϕ​能够估算出导致从 s t s_t st​到 s t + 1 s_{t+1} st+1​状态转变的行动 a t a_t at​。这可以用公式 a t : = f ϕ ( s t , s t + 1 ) a_t := f_\phi(s_t, s_{t+1}) at​:=fϕ​(st​,st+1​)表示。

        逆向动力学模型是一种基于学习的方法，它试图从结果（即状态变化）反推原因（即行动）。这与传统的动力学模型不同，后者通常从给定的行动预测结果状态。在机器学习和强化学习中，逆向动力学模型通常通过监督学习训练，其中训练数据包括状态对和相应的行动。

        例如，在机器人控制的应用中，如果已知机器人从位置A移动到位置B，逆向动力学模型可以被用来推断出使机器人从A移动到B的具体行动，如转动的角度、速度等。这种方法使得可以从状态变化中直接提取行动信息，对于那些直接的行动数据不易获取或模拟的场景尤为有用。

        逆向动力学模型通常是一个神经网络。在强化学习和机器学习的应用中，这种模型通过学习从结果状态反推行动的关系，从而能够从观察到的状态变化中推断出导致这种变化的行动。神经网络的强大学习能力使其非常适合处理这类复杂的模式识别和推断任务。

        在实际应用中，这种神经网络模型会被训练，使其能够接受连续的状态对（如 s t s_t st​ 和 s t + 1 s_{t+1} st+1​)作为输入，并输出导致状态从 s t s_t st​转变到 s t + 1 s_{t+1} st+1​的行动 a t a_t at​。训练数据通常由真实的状态转换和相应的行动组成，使得网络能够通过监督学习方法学习这种映射关系。

        无分类器指导规划（Planning with Classifier-Free Guidance）

        无分类器指导规划（Planning with Classifier-Free Guidance）是一种用于规划和生成轨迹的方法，它避免了使用传统的分类器或动态规划过程。在决策扩散器中，这种方法被用于条件扩散模型，用于生成更高质量的轨迹。

        无分类器指导规划的工作方式如下：

        1. 条件化扩散过程：首先，扩散模型需要在特定特征 y ( τ ) y(\tau) y(τ)上进行条件化。这些特征可以是轨迹下的回报、满足特定约束的状态序列等。

        2. 避免动态规划：传统上，可以通过训练一个分类器 p ϕ ( y ( τ ) ∣ x k ( τ ) ) p_\phi(y(\tau)|x_k(\tau)) pϕ​(y(τ)∣xk​(τ))来从带噪声的轨迹 x k ( τ ) x_k(\tau) xk​(τ)中预测 y ( τ ) y(\tau) y(τ)。但这通常涉及估算 Q-函数，需要复杂的动态规划过程。

        3. 使用无分类器指导：为了避免这种复杂性，决策扩散器采用了无分类器指导，结合低温度采样。这允许从数据集中提取高概率轨迹，而不需要依赖于复杂的分类器或动态规划。

        举例说明：假设有一个机器人导航任务，目标是生成一条从起点到终点的最优轨迹。在无分类器指导规划中，扩散模型会被条件化，以优先生成那些高回报的轨迹。通过低温度采样，模型能够更集中地探索那些高质量、高可能性的轨迹，而无需通过复杂的分类器或Q-值估算来明确指导这一过程。这使得模型能够高效地生成满足特定目标或约束的轨迹，同时避免了传统方法中常见的计算复杂性。

        无分类器指导（Classifier-Free Guidance）是一种在条件生成模型中使用的技术，尤其是在条件生成扩散模型中。它允许模型在不使用明确的分类器模型来指导生成过程的情况下，生成满足特定条件的样本。这种方法特别适用于那些条件是难以分类的或是分类器可能会引入偏差的情况。

        在规划中，无分类器指导通常涉及以下步骤：

        1. 训练：训练一个条件生成模型，该模型能够生成在给定条件下的样本，如轨迹的某个特定特性（例如，高回报或满足某些约束的轨迹）。

        2. 权重调整：在生成过程中，对条件的影响进行权重调整。具体地说，模型会生成两组预测：一组在无条件下生成的，另一组在特定条件下生成的。

        3. 合成输出：最终的输出是两组预测的组合，通常是加权差，其中权重参数用于控制条件的影响强度。

        4. 提高样本质量：通过调整权重参数（通常在实验中确定），可以促使模型更倾向于生成具有高概率的（即更可能在数据集中出现的）样本。

        5. 避免复杂的分类器训练：这种方法避免了直接训练一个复杂的分类器来识别轨迹的特性，降低了模型复杂性和训练成本。

        举例来说，在规划一条路径时，无分类器指导可以帮助生成模型更有可能生成通往目的地而不违反交通规则的轨迹。这通过调整模型的权重参数来增加那些在训练数据中标记为合规且高效的轨迹的生成概率来实现。这样，即使在模型从未显式学习过特定分类任务的情况下，也能够生成高质量的规划结果。

        超越回报的条件化（Conditioning Beyond Returns）

        “超越回报的条件化（Conditioning Beyond Returns）”是一种在条件生成模型中使用的技术，用于生成不仅仅是最大化回报，还可以满足特定条件或展示特定行为的状态序列。它使得生成模型能够在考虑更多轨迹特性的同时进行规划，这些特性可以是满足某些约束或展现某些预定行为。

        具体的工作流程如下：

        1. 最大化回报：为了生成最大化回报的轨迹，模型会被条件化以考虑轨迹的回报 R ( τ ) R(\tau) R(τ)，并将回报归一化到 [0, 1] 区间。条件化噪声模型可以表示为 ϵ θ ( x k ( τ ) , R ( τ ) , k ) \epsilon_\theta(x_k(\tau), R(\tau), k) ϵθ​(xk​(τ),R(τ),k)，其中高回报轨迹的条件化可以认为是在 R ( τ ) = 1 R(\tau) = 1 R(τ)=1条件下。

        2. 满足约束：轨迹还可以满足多种约束，每种约束由集合 C i C_i Ci​表示，比如达到特定目标、按特定顺序访问状态，或避免状态空间的特定部分。为了生成满足给定约束 C i C_i Ci​的轨迹，模型同样会被条件化，使用一种独热编码来表示约束 ϵ θ ( x k ( τ ) , 1 ( τ ∈ C i ) , k ) \epsilon_\theta(x_k(\tau), 1(\tau \in C_i), k) ϵθ​(xk​(τ),1(τ∈Ci​),k)。

        3. 训练与推理：在训练阶段，模型使用包含单一约束的轨迹的离线数据集进行训练。在推理（或生成）阶段，模型可以被用来生成同时满足多个约束的轨迹。

        通过这种方式，“超越回报的条件化”使得扩散模型能够在生成过程中考虑更复杂的目标和约束，而不只是简单地最大化回报，从而在各种规划任务中提供更灵活和实用的解决方案。

        训练与实现细节

        决策扩散器（Decision Diffuser）的训练过程是以监督方式进行的。下面是其详细的训练过程和损失函数，以及实现细节：

        1. 训练数据集：给定一个包含轨迹的数据集 D D D，每条轨迹都标记了它实现的回报、它满足的约束或它展示的技能。

        2. 损失函数：训练反向扩散过程 p θ p_\theta pθ​（通过噪声模型 ϵ θ \epsilon_\theta ϵθ​ 参数化）和逆向动力学模型 f ϕ f_\phi fϕ​使用的损失函数 L ( θ , ϕ ) L(\theta, \phi) L(θ,ϕ) 定义为：

           L ( θ , ϕ ) : = E τ ∈ D , β ∼ Bern ( p ) [ ∣ ∣ ϵ − ϵ θ ( x k ( τ ) , ( 1 − β ) y ( τ ) + β ∅ , k ) ∣ ∣ 2 ] + E ( s , a , s ′ ) ∈ D [ ∣ ∣ a − f ϕ ( s , s ′ ) ∣ ∣ 2 ] L(\theta, \phi) := \mathbb{E}_{\tau \in D, \beta \sim \text{Bern}(p)} \left[ ||\epsilon - \epsilon_\theta(x_k(\tau), (1-\beta)y(\tau)+\beta\emptyset, k)||^2 \right] + \mathbb{E}_{(s,a,s') \in D} \left[ ||a - f_\phi(s, s')||^2 \right] L(θ,ϕ):=Eτ∈D,β∼Bern(p)​[∣∣ϵ−ϵθ​(xk​(τ),(1−β)y(τ)+β∅,k)∣∣2]+E(s,a,s′)∈D​[∣∣a−fϕ​(s,s′)∣∣2]

           这个损失函数有两部分组成：

           • 第一项是噪声预测的均方误差，它度量了模型预测的噪声 ϵ ^ θ \hat{\epsilon}_\theta ϵ^θ​与实际噪声 ϵ \epsilon ϵ 之间的差异。
           • 第二项是逆向动力学预测的均方误差，它度量了模型预测的行动 f ϕ ( s , s ′ ) f_\phi(s, s') fϕ​(s,s′) 与实际行动 a a a之间的差异。

           • 训练过程：

             • 对于每个轨迹 τ \tau τ，首先从正态分布中采样噪声 ϵ ∼ N ( 0 , I ) \epsilon \sim N(0, I) ϵ∼N(0,I)和时间步 k ∼ U { 1 , … , K } k \sim U\{1, \ldots, K\} k∼U{1,…,K}。
             • 然后构造带噪声的状态数组 x k ( τ ) x_k(\tau) xk​(τ)并预测噪声为 ϵ ^ θ : = ϵ θ ( x k ( τ ) , y ( τ ) , k ) \hat{\epsilon}_\theta := \epsilon_\theta(x_k(\tau), y(\tau), k) ϵ^θ​:=ϵθ​(xk​(τ),y(τ),k)。
             • 以概率 p p p忽略条件信息 y ( τ ) y(\tau) y(τ)，并且逆向动力学是用单个转换而不是轨迹进行训练的。

             • 模型架构：

               • e p s i l o n θ epsilon_\theta epsilonθ​通过时序U-Net架构参数化，这是一个包含重复的卷积残差块的神经网络。
               • 该架构将状态序列 x k ( τ ) x_k(\tau) xk​(τ)视为图像，其中高度代表单个状态的维度，宽度表示轨迹的长度。
               • 条件信息 y ( τ ) y(\tau) y(τ)编码为标量或独热向量，并投影到潜在变量 z z z中。

        这个训练过程和损失函数的设计旨在使决策扩散器能够学习如何根据过去的状态和当前的条件信息生成未来的状态序列，并通过逆向动力学模型预测导致状态转变的行动。这样的设计允许模型在各种条件下进行有效的规划和决策制定。

        低温度采样（Low-temperature Sampling）

        低温度采样（Low-temperature Sampling）是一种在生成模型中使用的技术，特别是在条件生成模型如扩散模型中。在这个上下文中，"温度"是一个控制随机性程度的超参数。在标准的采样过程中，生成的样本通常是从模型的输出分布中直接采样得到的。如果这个分布是高斯分布，那么它的形式是 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2)，其中 μ \mu μ是均值， σ 2 \sigma^2 σ2是方差（或温度）。

        在低温度采样中，温度参数被设定得比标准采样低，这通常通过减小方差来实现。这样做的效果是让模型生成的样本更接近于分布的均值，减少了采样过程中的随机性，从而产生更加确定性和高质量的输出。

        在扩散模型中，低温度采样可能会被用来控制生成过程中的噪声水平，使得生成的样本更加准确地反映训练数据的特性，特别是在生成尖锐的、详细的或结构化的输出时特别有用。这可以在图像生成中生成更清晰的图像，在文本生成中生成更连贯的文本，在音频生成中产生更清晰的音频样本等等。