文章目录
- 一、概要
- 二、概念
- 三、实验
- 四、代码
- 五、结果与总结
一、概要
介绍交叉熵损失函数(对数似然损失函数)的概念,并用酒驾数据集训练对率回归模型,并用召回率、精度、F1值等指标评估其分类性能。
二、概念
在二分类问题中,使用交叉熵损失函数训练对率回归模型时,损失函数可以表示为:
对于一个给定的样本x和其对应的标签 y(y取值为 0 或 1),模型输出的是一个介于 0 到 1 之间的预测概率 p,即 p = P(Y=1 | x; θ),其中θ表示模型参数。
交叉熵损失函数(也称为对数似然损失函数)的数学表达式如下:
L(y,p)=−[y⋅log(p)+(1−y)⋅log(1−p)]
解释:
- 当实际标签 (y = 1) 时,模型希望 (p) 接近 1,因此损失函数会尽量减小−log(p);
- 当实际标签 (y = 0) 时,模型希望 (p) 接近 0,因此损失函数会尽量减小 −log(1 - p)。
在整个训练集中,总的交叉熵损失函数是各个样本损失之和除以样本数量:

其中,(N) 是训练集中的样本数量, 是第 (i) 个样本的真实标签,(p_i) 是模型对第 (i) 个样本预测为正类的概率。
三、实验
现在我们有一个酒驾数据集,其中包含了驾驶员的相关特征(如年龄、饮酒量、驾驶时间等)和是否酒驾的结果标签。我们可以利用交叉熵损失函数训练一个对率回归模型(Logistic Regression)来预测驾驶员是否存在酒驾行为。
训练完成后,我们会用测试集评估模型的分类性能,常用的评估指标包括:
1、召回率(Recall):也称为灵敏度(Sensitivity),表示模型识别出的正例占所有实际正例的比例。

其中,TP(True Positive)为真阳性,FN(False Negative)为假阴性。
2、精度(Precision):表示模型识别出的正例中有多少确实是正例的比例。

其中,FP(False Positive)为假阳性。
3、F1值(F1 Score):是召回率和精度的调和平均数,综合反映了这两方面的性能。

通过计算以上指标,我们可以全面评价对率回归模型在酒驾识别任务上的性能好坏。通常情况下,针对此类问题,模型的性能评估还需要结合实际应用场景和业务需求,例如在涉及公共安全的应用场景下,可能更注重高召回率以减少漏报的情况。
四、代码
数据集已上传啦
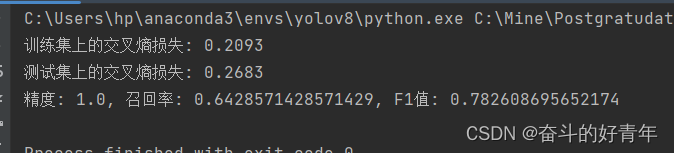
import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.metrics import precision_score, recall_score, f1_score, log_loss # 加载数据 df = pd.read_csv('alcohol_dataset.csv') # 选择特征和标签 X = df[['ALCOHOL', 'TEMP_AMB', 'TEMP_FAC_MAX', 'TEMP_FAC_MIN', 'EYES']].values y = df['LABEL'].astype(int).values # 划分训练集和测试集250个数据集, X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=134, random_state=42) # 特征缩放 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) class LogisticRegression: def __init__(self, learning_rate=0.01, n_iterations=1000): self.learning_rate = learning_rate self.n_iterations = n_iterations self.weights = np.random.randn(X_train_scaled.shape[1] + 1) # 包括偏置项 def add_intercept(self, X): return np.hstack([np.ones((X.shape[0], 1)), X]) def sigmoid(self, z): return 1 / (1 + np.exp(-z)) def predict_proba(self, X): X_with_bias = self.add_intercept(X) z = np.dot(X_with_bias, self.weights) return self.sigmoid(z) def predict(self, X, threshold=0.5): probas = self.predict_proba(X) return (probas >= threshold).astype(int) def fit(self, X, y): X_with_bias = self.add_intercept(X) for _ in range(self.n_iterations): z = np.dot(X_with_bias, self.weights) predictions = self.sigmoid(z) # 计算交叉熵损失 loss = -np.mean(y * np.log(predictions) + (1 - y) * np.log(1 - predictions)) # 计算梯度 gradient = np.dot(X_with_bias.T, (predictions - y)) / y.size # 更新权重 self.weights -= self.learning_rate * gradient return loss # 训练模型 model = LogisticRegression(learning_rate=0.01, n_iterations=1000) train_loss = model.fit(X_train_scaled, y_train) # 预测和评估 y_pred = model.predict(X_test_scaled) precision = precision_score(y_test, y_pred) recall = recall_score(y_test, y_pred) f1 = f1_score(y_test, y_pred) test_loss = log_loss(y_test, model.predict_proba(X_test_scaled)) print(f'训练集上的交叉熵损失: {train_loss:.4f}') print(f'测试集上的交叉熵损失: {test_loss:.4f}') print(f'精度: {precision}, 召回率: {recall}, F1值: {f1}')五、结果与总结