回顧
作爲這個系列文章的最後一篇，咱們先回顧一下建立神經網絡的整體步驟，以實現對機器學習神經網絡的整體認知：
在人工智能領域中，機器學習神經網絡的數據訓練部分是指通過将大量的輸入數據輸入到神經網絡中，利用反向傳播算法來調整網絡中的參數，從而使得網絡能夠學習到輸入數據的特征和模式。
數據訓練部分通常包括以下幾個步驟：
-
數據準備：首先要準備大量的标注數據，這些數據有已知的輸入和輸出值。輸入數據通常是一組向量或矩陣的形式，輸出數據可以是分類标簽、連續值等。同時，還需要将數據集劃分爲訓練集、驗證集和測試集。
-
初始化參數：神經網絡中的參數（權重和偏置）需要進行初始化，可以使用随機數或者其他方法。
-
前向傳播：将輸入數據通過網絡的每一層傳遞，并計算輸出。每一層的輸出都是下一層的輸入，直到到達輸出層。
-
計算損失：将網絡的輸出與真實值進行比較，通過某種損失函數來計算網絡輸出與真實值之間的差異。
-
反向傳播：根據損失函數的計算結果，通過鏈式法則計算每個參數對損失函數的梯度。
-
參數更新：根據計算得到的梯度，使用優化算法（如随機梯度下降）來更新網絡中的參數，目的是使損失函數逐漸減小。
-
重複叠代：以上步驟是一個叠代過程，通過多次叠代來逐步優化網絡的參數，使得網絡能夠更好地拟合輸入數據。
-
模型評估：使用驗證集來評估訓練後的模型的性能，可以計算準确率、精确率、召回率等指标。
-
測試模型：最後使用獨立的測試集來評估模型的泛化能力，即模型對未見過的數據的預測能力。
數據訓練部分的目的是通過大量的數據和反向傳播算法來調整網絡參數，使得網絡能夠學習到輸入數據的特征和模式，從而實現對未知數據的準确預測或分類。
第一次看到這個系列的小夥伴，可以看一下我這個系列的前面幾篇文章：
政安晨：【完全零基礎】認知人工智能（一）【超級簡單】的【機器學習神經網絡】 —— 預測機
https://blog.csdn.net/snowdenkeke/article/details/136139504政安晨：【完全零基礎】認知人工智能（二）【超級簡單】的【機器學習神經網絡】—— 底層算法https://blog.csdn.net/snowdenkeke/article/details/136141888政安晨：【完全零基礎】認知人工智能（三）【超級簡單】的【機器學習神經網絡】—— 三層神經網絡示例https://blog.csdn.net/snowdenkeke/article/details/136151970政安晨：【完全零基礎】認知人工智能（四）【超級簡單】的【機器學習神經網絡】—— 權重矩陣https://blog.csdn.net/snowdenkeke/article/details/136160424
誤差
神經網絡的輸出是一個極其複雜困難的函數，這個函數具有許多參數影響到其輸出的鏈接權重。
我們可以使用梯度下降法，計算出正确的權重嗎？
隻要我們選擇了合适的誤差函數，這是完全可以的。神經網絡本身的輸出函數不是一個誤差函數。但我們知道，由于誤差是目标訓練值與實際輸出值之間的差值，因此我們可以很容易地把輸出函數變成誤差函數。
咱們再仔細觀察一下如下表格（這是3個輸出節點的目标值和實際值以及誤差函數的候選項）：
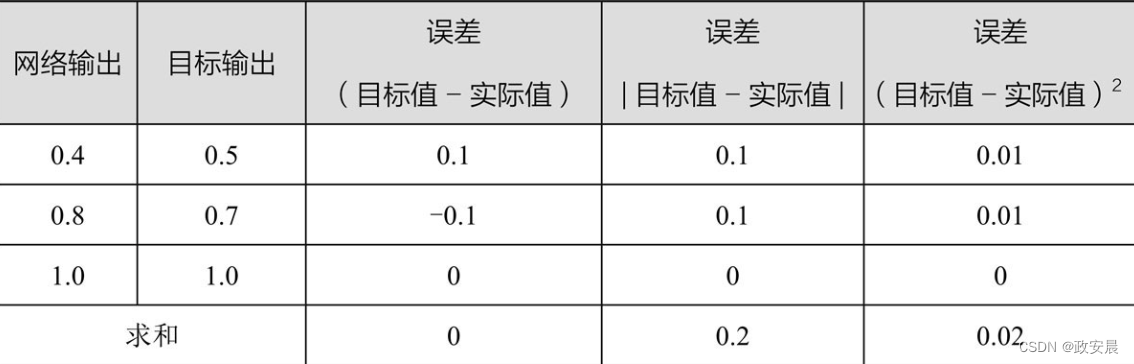
誤差函數的第一個候選項是（目标值-實際值），非常簡單。這似乎足夠合理了，對吧？
如果你觀察對所有節點的誤差之和，以判斷此時網絡是否得到了很好的訓練，你會看到總和爲0！
這是如何發生的呢？
A -
很顯然，由于前兩個節點的輸出值與目标值不同，這個網絡沒有得到很好的訓練。但是，由于正負誤差相互抵消，我們得到誤差總和爲0。總和爲零意味着沒有誤差。然而即使正負誤差沒有完全互相抵消，這也很明顯不符合實際情況，由此你也可以明白這不是一個很好的測量方法。
B -
爲了糾正這一點，我們采用差的絕對值，即将其寫成|目标值-實際值|，這意味着我們可以無視符号。由于誤差不能互相抵消，這可能行得通。由于斜率在最小值附近不是連續的，這使得梯度下降方法無法很好地發揮作用，由于這個誤差函數，我們會在V形山谷附近來回跳動，因此這個誤差函數沒有得到廣泛應用。在這種情況下，即使接近了最小值，斜率也不會變得更小，因此我們的步長也不會變得更小，這意味着我們有超調的風險。
C -
第三種選擇是差的平方，即（目标值-實際值）2。我們更喜歡使用第三種誤差函數，而不喜歡使用第二種誤差函數，原因有以下幾點：
· 使用誤差的平方，我們可以很容易使用代數計算出梯度下降的斜率。
· 誤差函數平滑連續，這使得梯度下降法很好地發揮作用—沒有間斷，也沒有突然的跳躍。
· 越接近最小值，梯度越小，這意味着，如果我們使用這個函數調節步長，超調的風險就會變得較小。
是否有第四個選項呢？
有，你可以構造各種各樣的複雜有趣的代價函數。一些函數可能完全行不通，一些函數可能對特定類型的問題起作用，一些能夠發揮作用的函數，可能由于額外的複雜度而有點不值得。
要使用梯度下降的方法，現在我們需要計算出誤差函數相對于權重的斜率。
這需要微積分的知識，微積分使用精确的數學方式，計算出當一些變量改變時，其他應變量如何改變。例如，當在彈簧上施加一個伸展力時，彈簧的長度如何變化。
此處，我們感興趣的是，誤差函數是如何依賴于神經網絡中的鏈接權重的。詢問這個問題的另一種方式是—“誤差對鏈接權重的改變有多敏感？”
咱們看下圖：
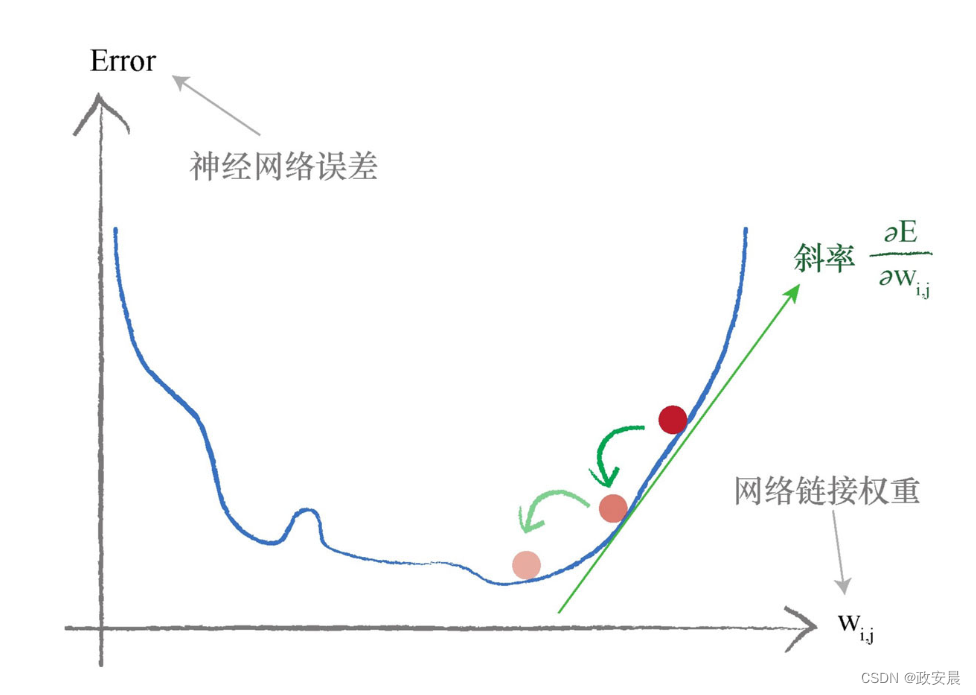
我們希望最小化的是神經網絡的誤差函數。我們試圖優化的參數是網絡鏈接權重。
在這個簡單的例子中，我們隻演示了一個權重，但是我們知道神經網絡有衆多權重參數。
下圖顯示了兩個鏈接權重，這次，誤差函數是三維曲面，這個曲面随着兩個鏈接權重的變化而變化。你可以看到，我們努力最小化誤差，現在，這有點像咱們這個系列第四篇文章提到的：在多山的地形中尋找一個山谷。
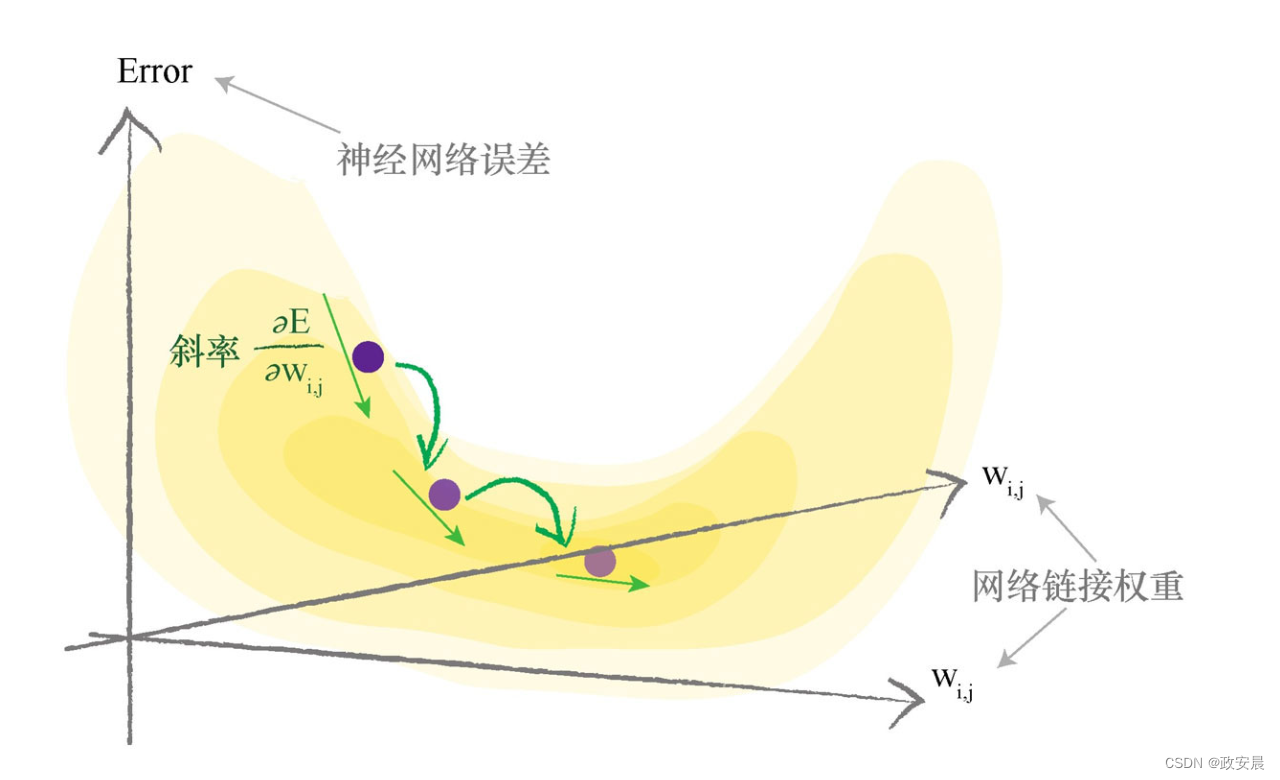
當函數具有多個參數時，要畫出誤差曲面相對較難，但是使用梯度下降尋找最小值的思想是相同的。
讓我們使用數學的方式，寫下想要取得的目标：
這個表達式表示了當權重wj,k改變時，誤差E是如何改變的。這是誤差函數的斜率，也就是我們希望使用梯度下降的方法到達最小值的方向。
在我們求解表達式之前，讓我們隻關注隐藏層和最終輸出層之間的鏈接權重。下圖突出顯示了咱們所感興趣的這個區域。我們将重回輸入層和隐藏層之間的鏈接權重。
在進行微積分計算時，我們會時不時地返回來參照此圖，以确保我們沒有忘記每個符号的真正含義。小夥伴們不要被吓倒而裹足不前，這個過程并不困難，咱們在這個系列以前的文章中已經介紹了所有所需的概念。
首先，讓我們展開誤差函數，這是對目标值和實際值之差的平方進行求和，這是針對所有n個輸出節點的和：
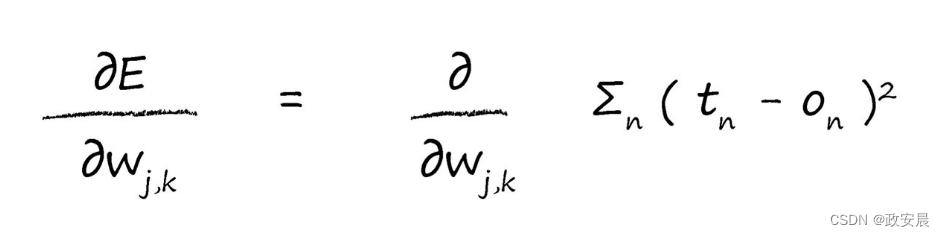
此處，我們所做的一切，就是寫下實際的誤差函數E。
注意，在節點n的輸出隻取決于連接到這個節點的鏈接，因此我們可以直接簡化這個表達式。這意味着，由于這些權重是鏈接到節點k的權重，因此節點k的輸出
隻取決于權重wj,k。
咱們可以使用另一種方式來看待這個問題，節點k的輸出不依賴于權重wj,b，其中，由于b和k之間沒有鏈接，因此b與k無關聯。權重wj,b是連接輸出節點b的鏈接權重，而不是輸出節點k的鏈接權重。
這意味着，除了權重wj,k所鏈接的節點（也就是）外，我們可以從和中删除所有的
，這就完全删除了令人厭煩的求和運算。這是一個很有用的技巧，值得保留下來收入囊中。
這意味着誤差函數根本就不需要對所有輸出節點求和。原因是節點的輸出隻取決于所連接的鏈接，就是取決于鏈接權重。這個過程在許多教科書中一略而過，這些教科書隻是簡單地聲明了誤差函數，卻沒有解釋原因。
無論如何，咱們現在有了一個相對簡單的表達式了。
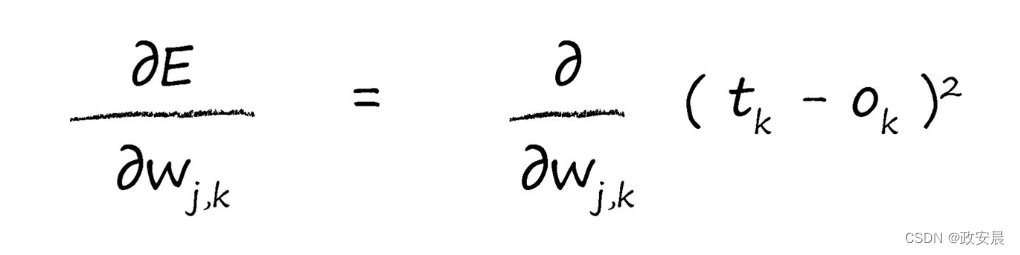
現在，我們将進行一點微積分計算。
的部分是一個常數，因此它不會随着wj,k的變化而變化。也就是說，
不是wj,k的函數。仔細想想，如果真實示例所提供的目标值根據權重變化，就太讓人匪夷所思了！由于我們使用權重前饋信号，得到輸出值
，因此這個表達式留下了我們所知的依賴于wj,k的
部分。我們将使用鏈式法則，将這個微積分任務分解成更多易于管理的小塊。
我們将使用鏈式法則，将這個微積分任務分解成更多易于管理的小塊。
再看一下鏈式法則：
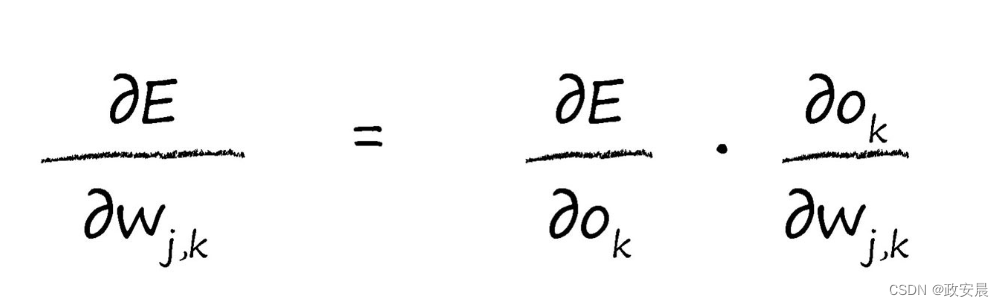
現在，我們可以反過來對相對簡單的部分各個擊破，我們對平方函數進行簡單的微分，就很容易擊破了第一個簡單的項。這使我們得到了以下的式子：
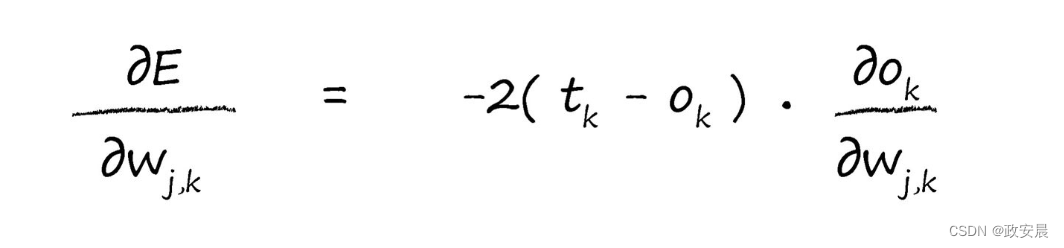
對于第二項，我們需要仔細考慮一下，但是無需考慮過久。是節點k的輸出，如果你還記得，這是在連接輸入信号上進行加權求和，在所得到結果上應用S函數得到的結果。讓我們将這寫下來，清楚地表達出來：
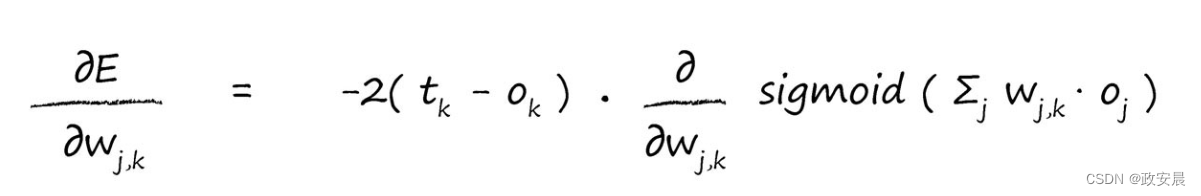
是前一個隐藏層節點的輸出，而不是最終層的輸出
。
對S函數求微分，這對我們而言是一種非常艱辛的方法，但是，其他人已經完成了這項工作。我們可以隻使用衆所周知的答案，就像全世界的數學家每天都在做的事情一樣即可（細節這裏不贅述啦）。
在微分後，一些函數變成了非常可怕的表達式，S函數微分後，可以得到一個非常簡單、易于使用的結果。在神經網絡中，這是S函數成爲大受歡迎的激活函數的一個重要原因。
因此，讓我們應用這個酷炫的結果，得到以下的表達式：
這個額外的最後一項是什麽呢？由于在sigmoid()函數内部的表達式也需要對進行微分，因此我們對S函數微分項再次應用鏈式法則。這也非常容易，答案很簡單，爲
。
在寫下最後的答案之前，讓我們把在前面的2去掉，我們隻對誤差函數的斜率方向感興趣，這樣我們就可以使用梯度下降的方法，因此可以去掉2。隻要我們牢牢記住需要什麽，在表達式前面的常數，無論是2、3還是100，都無關緊要。因此，去掉這個常數，讓事情變得簡單。
這就是我們一直在努力要得到的最後答案，這個表達式描述了誤差函數的斜率，這樣我們就可以調整權重了：
這就是我們一直在尋找的神奇表達式，也是訓練神經網絡的關鍵。
這個表達式值得再次回味，顔色标記有助于顯示出表達式的各個部分。
第一部分，非常簡單，就是（目标值-實際值），我們對此已經很清楚了。
在sigmoid中的求和表達式也很簡單，就是進入最後一層節點的信号，我們可以稱之爲ik，這樣它看起來比較簡單。這是應用激活函數之前，進入節點的信号。
最後一部分是前一隐藏層節點j的輸出。讀者要有一種意識，明白在這個斜率的表達式中，實際涉及哪些信息并最終優化了權重，因此小夥伴們值得仔細觀察這些表達式、這些項。
咱們還需要做最後一件事情。我們所得到的這個表達式，是爲了優化隐藏層和輸出層之間的權重。現在，我們需要完成工作，爲輸入層和隐藏層之間的權重找到類似的誤差斜率。
同樣，我們可以進行大量的代數運算，但是不必這樣做。我們可以很簡單地使用剛才所做的解釋，爲感興趣的新權重集重新構建一個表達式：
· 第一部分的（目标值-實際值）誤差，現在變成了隐藏層節點中重組的向後傳播誤差，正如在前面所看到的那樣。我們稱之爲ej。
· sigmoid部分可以保持不變，但是内部的求和表達式指的是前一層，因此求和的範圍是所有由權重調節的進入隐藏層節點j的輸入。我們可以稱之爲ij。
· 現在，最後一部分是第一層節點的輸出oi，這碰巧是輸入信号。
這種巧妙的方法，簡單利用問題中的對稱性構建了一個新的表達式，避免了大量的工作。這種方法雖然很簡單，但卻是一種很強大的技術，一些天賦異禀的數學家和科學家都使用這種技術。你肯定可以使用這個技術，給你的隊友留下深刻印象。
因此，我們一直在努力達成的最終答案的第二部分如下所示，這是我們所得到誤差函數斜率，用于輸入層和隐藏層之間權重調整。
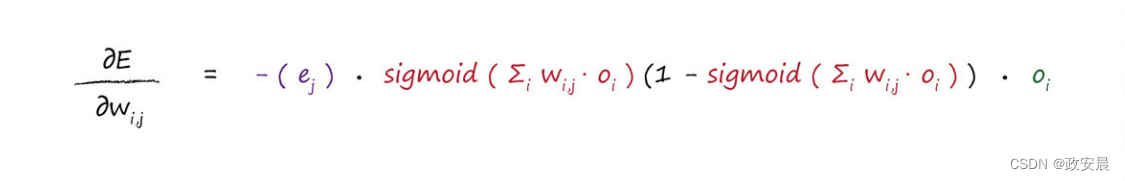
現在，我們得到了關于斜率的所有關鍵的神奇表達式，可以使用這些表達式，在應用每層訓練樣本後，更新權重，在接下來的内容中我們将會看到這一點。
記住權重改變的方向與梯度方向相反，正如我們在先前的圖中清楚看到的一樣。我們使用學習因子，調節變化，我們可以根據特定的問題，調整這個學習因子。當我們建立線性分類器，作爲避免被錯誤的訓練樣本拉得太遠的一種方式，同時也爲了保證權重不會由于持續的超調而在最小值附近來回擺動，我們都發現了這個學習因子。讓我們用數學的形式來表達這個因子。
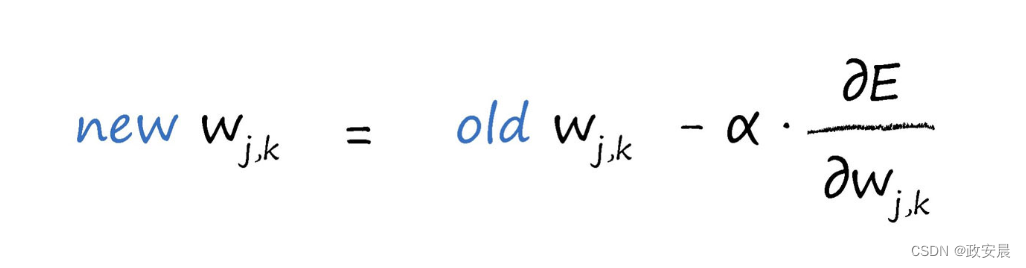
更新後的權重wj, k是由剛剛得到誤差斜率取反來調整舊的權重而得到的。正如我們先前所看到的，如果斜率爲正，我們希望減小權重，如果斜率爲負，我們希望增加權重，因此，我們要對斜率取反。符号α是一個因子，這個因子可以調節這些變化的強度，确保不會超調。我們通常稱這個因子爲學習率。
這個表達式不僅适用于隐藏層和輸出層之間的權重，而且适用于輸入層和隐藏層之間的權重。差值就是誤差梯度，我們可以使用上述兩個表達式來計算這個誤差梯度。
如果我們試圖按照矩陣乘法的形式進行運算，那麽我們需要看看計算的過程。爲了有助于理解，我們将按照以前那樣寫出權重變化矩陣的每個元素。
由于學習率隻是一個常數，并沒有真正改變如何組織矩陣乘法，因此我們省略了學習率α。
權重改變矩陣中包含的值，這些值可以調整鏈接權重wj, k，這個權重鏈接了當前層節點j與下一層節點k。你可以發現，表達式中的第一項使用下一層（節點k）的值，最後一項使用前一層（節點j）的值。
仔細觀察上圖，你就會發現，表達式的最後一部分，也就是單行的水平矩陣，是前一層oj的輸出的轉置。顔色标記顯示點乘是正确的方式。如果你不能确定，請嘗試使用另一種方式的點乘，你會發現這是行不通的。
因此，權重更新矩陣有如下的矩陣形式，這種形式可以讓我們通過計算機編程語言高效地實現矩陣運算。
實際上，這不是什麽複雜的表達式。由于我們簡化了節點輸出，那些sigmoids已經消失了。
示例
我們來演示幾個有數字的示例，讓讀者看看這種權重更新的方法是可以成功的。下面的網絡是我們之前演示過的一個，但是這次，我們添加了隐藏層第一個節點oj=1和隐藏層第二個節點oj=2的示例輸出值。這些數字隻是爲了詳細說明這個方法而随意列舉的，讀者不能通過輸入層前饋信号正确計算得到它們：
我們要更新隐藏層和輸出層之間的權重w1,1。當前，這個值爲2.0。
讓我們再次寫出誤差斜率（方便比照看）。
讓我們一項一項地進行運算：
· 第一項（tk-ok）得到誤差e1=0.8。
· S函數内的求和Σjwj,koj爲（2.0×0.4）+（3.0 * 0.5）=2.3。
· sigmoid 1/(1+e -2.3) 爲0.909。中間的表達式爲0.909 *（1-0.909）=0.083。
· 由于我們感興趣的是權重w1,1，其中j=1，因此最後一項oj也很簡單，也就是oj=1。此處，oj值就是0.4。
将這三項相乘，同時不要忘記表達式前的負号，最後我們得到-0.0265。
如果學習率爲0.1，那麽得出的改變量爲-（0.1 * -0.02650）=+0.002650。因此，新的w1,1就是原來的2.0加上0.00265等于2.00265。
雖然這是一個相當小的變化量，但權重經過成百上千次的叠代，最終會确定下來，達到一種布局，這樣訓練有素的神經網絡就會生成與訓練樣本中相同的輸出。
咱們就這樣完成了這個例子。
結論
1. 神經網絡的誤差是内部鏈接權重的函數。
2. 改進神經網絡，意味着通過改變權重減少這種誤差。
3. 直接選擇合适的權重太難了。另一種方法是，通過誤差函數的梯度下降，采取小步長，叠代地改進權重。所邁出的每一步的方向都是在當前位置向下斜率最大的方向，這就是所謂的梯度下降。
4. 使用微積分可以很容易地計算出誤差斜率。
至此，咱們已經完成了零基礎認知人工智能的神經網絡全系列的文章啦。
