文章目录
- 😏专栏导读
- 🤖文章导读
- 先导知识
- 🙀插入排序
- 代码实现
- 直接插入排序的特性总结
- 😳希尔排序(缩小增量排序)
- 代码实现
- 😳冒泡排序
- 代码实现
- 😳选择排序
- 代码实现
- 😳堆排序
- 代码实现
- 😳快速排序
- 代码实现(hoare版本)
- 😳归并排序
- 代码实现
- 😳计数排序
- 代码实现
- 总结
😏专栏导读
👻作者简介:M malloc,致力于成为嵌入式大牛的男人
👻专栏简介:本文收录于 初阶数据结构,本专栏主要内容讲述了初阶的数据结构,如顺序表,链表,栈,队列等等,专为小白打造的文章专栏。
👻相关专栏推荐:LeetCode刷题集,C语言每日一题。

🤖文章导读
本章我将详细的讲解关于八大排序的知识点

先导知识
在本篇文章中,我们将讨论将元素的数组排序的问题,为了方便理解,本篇文章的数组只包含整数。
我们对内部排序的考查将指出
- 存在几种容易的算法以 O(N²)排序,如插入排序。
- 有一种算法叫做希尔排序(ShellSort),它编程十分的简单,以O(N²)运行,并在实践中有效
- 有一些稍微复杂些的O(N*LogN)的排序算法
- 任何通用的排序算法均需要O(N*LogN)次比较
本章的其余部分将描述和分析各种排序算法。这些算法包含一些有趣的和重要的代码优化和算法设计思想,可以对排序做出精确的分析。预先说明,在适当的时候,我们将尽可能地多做一些分析。
🙀插入排序
最简单的排序算法之一是插入排序(insertion sort)。插人排序由N-1趟(pass)排序组成对于 i=1趟到 i=N - 1趟,插入排序保证从位置0 到位置i上的元素为已排序状态插入排序利用了这样的事实:位置0到位置 i-1上的元素是已排过序的。下图显示一个简单的数组在每一趟插人排序后的情况。
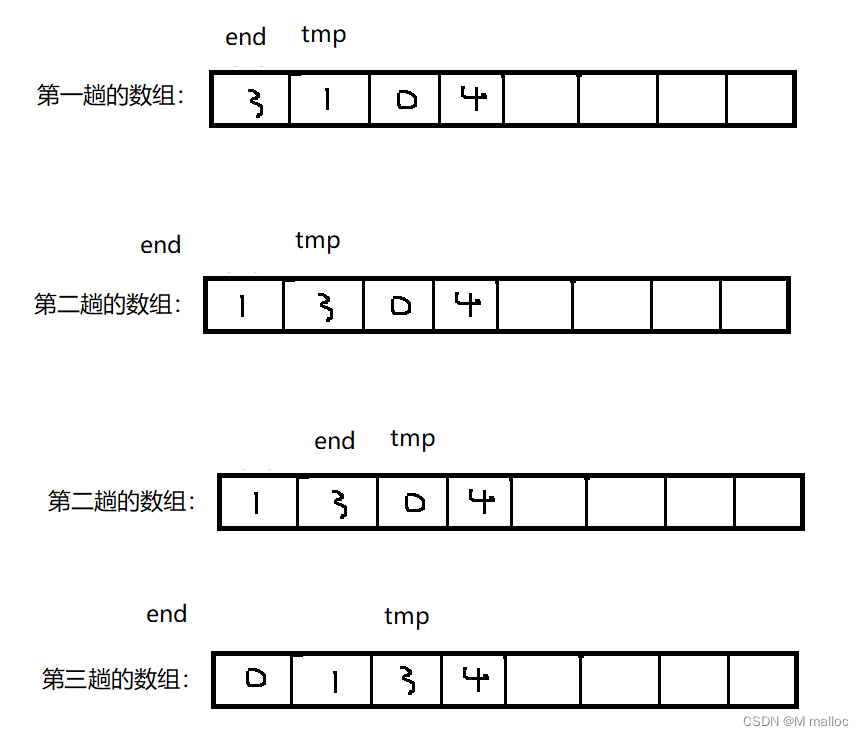
全部的思路就是以上的思路啦,就是我们需要从i位置进行比较,然后把大的数依次的往后移动,把小的数依次往前移动。这样排序排的就是升序下面是代码实现
代码实现
void InsertSort(int* a, int n) { for (int i = 1; i = 0) { if (a[end] > tmp) { a[end + 1] = a[end]; --end; } else { break; } } a[end + 1] = tmp; } }
直接插入排序的特性总结
- 元素集合越接近有序,直接插入排序算法的时间效率更高
- 时间复杂度:O(N²)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
😳希尔排序(缩小增量排序)
没想到吧,其实希尔排序也属于插入排序类的方法,但在时间效率上较上一种排序方法有较大的改进。
从对直接插入排序的分析得知,其算法时间复杂度为O(n²),但是,若待排序记录序列为正序时,其时间复杂度可提高至O(N)。
思想讲解
先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录”基本有序“时,再对全体记录进行一次直接插入排序。
代码实现
void ShellSort(int* a, int n) { //1、gap > 1 预排序 //2、gap == 1 直接插入排序 int gap = n; while (gap > 1) { gap = gap / 3 + 1; for (int i = 0; i = 0) { if (a[end] > tmp) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } }希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:
😳冒泡排序
冒泡排序就是一个老生常谈的话题了,这里就不细讲啦,因为我相信大家在学校里,老师基本上都会教这个算法,因为它是最容易上手滴,也是最容易理解的。其实冒泡排序还叫起泡排序。
时间复杂度:O(N²)
代码实现
void BubbleSort(int* a, int n) { for (int j = 0; j a[i]) { int tmp = a[i]; a[i] = a[i - 1]; a[i - 1] = tmp; Exchange = true; } } if (exchange == false) { break; } } }冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
😳选择排序
基本思想
每一趟在n-i-1(i=1,2,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。其中最简单且为人们所熟悉的时简单选择排序。
代码实现
void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } void SelectSort(int* a, int n) { int begin = 0, end = n - 1; while (begin直接选择排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
😳堆排序
只需要一个记录大小的辅助空间,每个待排序的记录仅占有一个存储空间。
代码实现
void AdjustDown(int* a, int n, int parent) { int child = parent * 2 + 1; while (child a[child]) { ++child; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } //排升序 N * logN void HeapSort(int* a, int n) { //建大堆 for (int i = (n - 1 - 1) / 2; i >= 0; i--) { AdjustDown(a, n, i); } int end = n - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); --end; } }直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
😳快速排序
快速排序是对起泡排序的一种改进。它的基本思想是,通过一趟排序将待排记录分割成独立的两部分,其中一个部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
代码实现(hoare版本)
int partSort(int* a, int left, int right) { int midi = GetMidIndex(a, left, right); Swap(&a[left], &a[midi]); int keyi = left; while (left left && a[right] >= a[keyi]) { --right; } //左边找大 while (right > left && a[left] ++left; } Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[right]); return left; } void QuickSort(int* a, int begin, int end) { if (begin = end) { return; } int keyi = partSort(a, begin, end); //[begin, keyi - 1] keyi [keyi + 1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); }快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
😳归并排序
归并排序是又一类不同的排序方法。"归并"的含义是将两个或两个以上的有序的有序表组合成一个新的有序表。它的实现方法早已为大家所熟悉,无论是顺序存储结构还是链表存储结构,都可在O(m+n)的时间量级上实现。利用归并的思想容易实现排序。
代码实现
void _mergeSort(int* a, int begin, int end, int* tmp) { if (begin == end) return; //小区间优化 if (end - begin + 1









